1. intra-universe: connects regions in the same Universe. These are the "classical" ones,
   like Wormhole types with names as "the Schwartzschild-", and "Einstein-Rosen" bridges.
   
2. inter-universe: some cosmological models deal with the "Multiverse". In the "baby Multiverse" model,
   Wormhole-like structures links multiple Universa.
   
3. Quantum Foam - Planck scale: At the lowest possible scale of SpaceTime, the "vacuum" might consists
   of a sort of foam of wormholes. It's a serious idea, under study by a few physicists.
   Interestingly, the latest "models" link those sort of wormholes to the Quantum Mechanical feature "Entanglement".

ä / a = - (4 π G) / 3 (p + 3ρ/c²)

Chapter 2. Some results of Einsteins General Relativity (GR).

Indeed..., just "some" results, since GR is a massive and complex framework. Everybody knows that Einstein was extremely
intelligent, and very involved in physics. So, what Einstein wrote down, is absolutely not "easy", so to speak.

In GR, Einstein developed his famous "field equations". One equation is this one:

G_uv + g_uv Λ = (8 π G/c⁴) Τ_uv

(or simplified : G_uv = (8 π G/c⁴) x Τ_uv     if Λ=0 )

Above we see (just) one of Einstein's "field equations" of his famous "Theory of General Relativity (GR)".

In GR, gravity has curvature effects on the four dimensions of the SpaceTime.
So, a large mass, will noticeably curve SpaceTime.

What the equation says, is actually how much curvature there is in any given region of space, due to "mass" in the vincinity.

The part on the left side of the "=" sign ( G_uv ), is a measure for the curvature of SpaceTime.

The part on the right side of the "=" sign ( Τ_uv ), is a measure of the amount, or density, of "mass" (or read "mass-energy").

So, the "amount" of curvature of SpaceTime is directly related to the mass.

Indeed, it's directly related, so: a small mass means a low curvature, and a high mass means a high curvature.

G_uv is the "Einstein tensor" and Τ_uv is the stress–energy (related to mass) tensor.

Let's clarify those tensors a bit. Einsteind solved the problem of gravity in geometrical way, using manifolds and tensors.

For example, a simple number, a scalar, can be used describe some physical properties like Temperature.
The temperature somewhere in a room, can be expressed by a simple number, a magnitude only (there is no further geometry).

Sometimes we need a vector to describe entities. For example, an Electric field has a magnitude and direction
at a certain point in space. Also, velocity has a magnitude and direction too.

However, sometimes an extended mathematical object is needed to describe stuff. For example, if you bend a piece of metal,
at any point inside, countless stress points exists, with different magnitudes and directions.
You can use a sort of "stress" tensor to describe the material in such a situation.

The "crux" is, that multiple "stresses" try to form the material to different directions, with "toroidal" (curving) effects,
and you cannot use a scalar, or vector, to describe that. Here, an mathematical extension, a "tensor", does the job.

A tensor can often be used to describe "Operators" (or mappings) too. Often you can write it as a "matrix".

Einstein was so brilliant to decribe gravity is a similar way. We have the curvature of points in SpaceTime, which
can be described by G_uv, all due to the "cause", which is the Τ_uv tensor that decribes the mass-energy distribution.

Actually, this is just (!) one of the many, many milestones, by Einstein, already developed in (around) 1915.

The equation above, also says something fundamentally (in a classical way) about Black holes (and the hypothetical Wormholes).

Suppose the "mass density" is extremely high, then the SpaceTime curvature close to that "mass density" is extremely high too, possibly up to
the point where the "strech" goes to infinity. Or in other words, "ds" as the distance metric, becomes asymptotic.
In case of a Black hole, nothing can escape anymore, not even light (in the GR framework).

Whenever a theory allow for a true singularity, physicists walk on their toes.

Many physicists think that "somehow", near the sigularity, a theory like General Relativity really has to be replaced by
something else, like "Quantum Gravity" (in fact, physicsts try to unify or reconcile, the different theories).

Chapter 3. A note on the "Schwarzschild distance" (or radius).

In chapter 1, we saw that if the "mass-density" would be very high, then the surrounding SpaceTime get's strongly curved too.
In the extreme, space would be streched so much, and gravity would be so high, that even light would not escape anymore.

This sort of "barrier" (where even light would not escape anymore), is also called a "horizon".

For example, I you would compress all of the mass of the Earth in into the size of a small marble (9 mm), then the escape velocity
from "Earth" would be the speed of light (c). In that case, the "horizon" would be 9 mm.

If you would do the same for the Sun, you need to compress all mass into a sphere of less than 3 km.

Karl Schwartzschild calculated a "horizon" for any mass ("M") compressed inside a critical radius r_s.
So, the "horizon" and "critical radius" is the same, actually.

This critical radius is called the "Schwarzschild radius". The full "exercise" is also called the "Schwarzschild solution".
When you, from the "outside", would move towards that radius, the curvature of spacetime increases, and the gravity strongly increases too.
At the Schwarzschild radius, the gravity is so strong that even light cannot escape anymore.

Actually, the sphere of the Schwarzschild radius (surrounding the mass) is called the "horizon" since you cannot "see" or observe
anything beyond that horizon. Essentially, it's a "black hole". Why? Because light cannot escape anymore from within that horizon.

Remember that "curvature" in spacetime geometry, has the effect of producing accelerations. Near the horizon, gravity get's so strong that
nothing can escape, not even light.

So, Schwartzschild went to work, armed with the insights produced by Einstein.
Schwartzschild reasoned: "Just imaging a spherical "horizon", with a very heavy mass ("M") inside, and spherical symmetric,
but strongly curved, spacetime surrouding it. Now, for that mass "M", which radius then is the horizon where it holds that
light cannot escape anymore?".

His theoretical framework used a few assumptions:

1. We have some mass concentration at some location, but no there is no other "stuff" elsewhere (outside the horizon), like another large mass.
2. The system under observation is Spherically symmetric and "time independent".
3. Most derivations uses "spherical coordinates" (r,θ,φ) instead of (x,y,z,t).
4. There is no angular momentum (of the mass) involved. That would complicate the derivation.
5. The "Λ" is assumed to be zero.
6. The solution is valid for outside the "Horizon" only.

Don't worry about them, esspecially about point 2. It just means that the system involved does not change in time:
We just have some steady mass inside some region, which does not grows bigger or gets smaller in time.

Why spherical coordinates? When you deal with a spherical symmetric system, then just like astronomers describe the postions of stars in
the heavens, or sea going folks use positions of stars to determine their location, it's just "natural" to use (r,θ,φ).
Don't you agree that this coordinate system fully describe any postion around the horizon?
You only need a radial distance "r", and two angles, to fully qualify any position in the space surrounding the mass.
However, if we "stay" in one plane only, we can eliminate one angle.

(1): We must also keep in mind, that at a great distance from the Horizon, the curvature is small or even going to flat space again.
Only when you get nearer and nearer towards the "Schwarzschild radius", the curvature gets larger and larger.

(2): Actually the same as (1), but we intuitively feel that the spacetime curvature should be dependent on "r".

(3): Actually, the spacetime curvature should be dependent on (r,θ,φ). But if we limit the solution
for a plane through the centre of Mass, then we can neglect φ
So, instead of studying all points in space around M (then we indeed need r,θ,φ), we just take an imaginary "plane"
where φ is zero. We can still calculate the curvature, but then limited from this "plane" only. However, that's good enough.

There is no need to reproduce the full "derivation" here. I will only show some formula's that were essential in his reasoning.
I am afraid that a full derivation would be utmost boring. So, we will not do that, and it's not neccessary at all!
We "trust" Schwartzschild, and the relation below is facinating. I will explain why it's "great", in a moment.

An important relation Schwartzschild found can be expressed like so:

ds ² = - (1 - 2M/r) dt² + dr² / (1 - 2M/r) + r²dθ²

Now, take a look at figure 1 below. Fig 1.



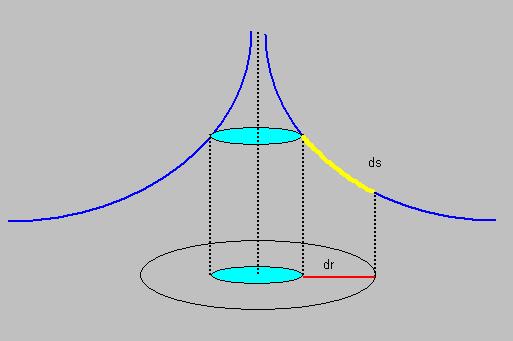
How to interpret figure 1?

Below in figure 1, you see some concentric circles, representing flat space, so, in this case, there is NO mass M in place.
You see a piece of lenght, called "dr". In fact, in this situation, just think of it as if those blue curved lines are not present in the figure.

Now, imagine we place a large "mass density" in the centre of those concentric circles. How space will be "curved",
is now expressed by the "blue" curved lines. The closer you go to the centre, the more asymptotically the blue lines become.
In this situation, where M is present in the centre of the concentric circles,
the piece of lenght, is now represented by "ds".

Note that now "ds" is longer than "dr", but actually is should be the same piece of space.
the length without the mass M (dr), and the length with the mass M (ds).

Again, note that the "lenght" ds represents a piece of curved space, that gets more curved the closer you go
to the mass "M".

Schwartzschild used the equation above, to finally arrive to a formula for the "Critical Radius":

r_s = 2 GM / c²

Where "G" is the gravitational constant, "c" is the speed of light, and "M" is the mass inside the critical radius.

For any mass "M" a critical Schwartzschild Radius r_s can be calculated, which defines the Horizon, and effectively
says when then mass becomes a "black hole". For example, if the Sun's mass were to be compressed within (about) 2 miles,
then it's a black hole.

Actually, the results are quite spectecular. Although the Einstein Field equations are the fundaments, here Schwarzschild found
a practical solution for a common situation.

Ok, now we have a little insight in the "critical" Schwartzschild Radius too.

Chapter 4. Do we have "Information Loss" at a Black Hole?

I like this subject to be part of this note, as to illustrate that physicists are still plagued with
open questions and paradoxes. And this subject is "just" one of those open questions.

For this specific issue, is there really a problem?
It depends a bit on your viewpoints. I have noticed that some physicists don't see much of an issue, while most others do.

It's not exactly a question for an IT expert. It is a problem in physics, and probably an interesting one for Philosophy too.

There are two scenario's people speak of. Let's see about them.

Scenario 1:

For the first time, we have a true and brutal "sink" in SpaceTime, which "slurps up" everything.
Anything falling in, has a certain "state" (a Quantum State if you will), which gets suddenly (?) lost if it enters the Black Hole.

If you like, you can take an example of an Quantum entangled system. Suppose one particle of the system flies into the Black Hole.
What happens with the state of the other free particle? Or what happens to both?

From ElectroMagnetic-, ThermoDynamic-, Nuclear-, Quantum Mechanical standpoints, there is some worries about "Information Loss".
However, it seems that the more "deterministic" elements enters some theory, the worries gets bigger and bigger.

For example, does the present state of a system determines the former and/or future states?

So, folks who believe that information is stored or encoded in some present state, view a Black Hole
as a possible demolisher of encoded information.

The "Information Loss" problem is felt to be extra painful if a "singularity" is involved.
Matter (and thus some sort of information) falls in the "singularity", and nothing changes over there?

Indeed, from a perspective of Quantum Mechanics, particles can be characterized by "states", and all interactions can be viewed
as state changes. Now, if a "sink" really destroys them into a singularity, in fact, something like Volume=0,
then that's tough to digest for physicists.

Mathematically, it can be deduced, as some claim, that if the surface of the "sphere of the horizon" grows,
while matter falls in, information "might" not be lost. In a way, states are collected in "some" manner.

Scenario 2:

Stephen Hawking proposed that a Black Hole "radiates", due to a special effect.

The vacuum is a strange place, really. Virtual particles (a particle and it's anti-particle) can "pop up",
and live for a very short time, before they annihilate each other, producing a photon.
You might interpret that as a consequence of one of Heisenberg's uncertainty relations, although some physicists
are critical to such statement. Since Δ E . Δ t > ℏ / 2, the vacuum can shortly "borrow" Energy
as long as the timespan is short enough.

Anyway, there is hardly any doubt on the existence of "virtual particles", since the clues theretoo are really plenty,
such as the "Casimir effect", or the "Zeemann effect" etc..

Now, when virtual particles are produced near the "critical Schwartzschild Radius", one particle may get "lost"
into the Black hole, while the other one "gets real" and escapes.
This just have to have impact on the Black hole, whether it be small or large, but it simply has to.

This one partner that goes into the Black hole must be "negative" Energy, since the one that escapes becomes real, and is positive.
Yes, the particle that survives is "normal", so has mass and thus Energy.

In other words, suppose a Black hole is on a diet, and does not "eat" matter any further, it will slowly "evaporate".
There is not much doubt on "Hawking radiation", but it's theoretical only (for now), although some simulations stronly
support it.

Now, there remains the question if "Hawking radiation" possibly solves the Information loss.
There seems consensus among physicists that it does not. At or near the Horizon of the Black Hole, a virtual pair is formed,
and one partner goes in, and the other partner escapes. It is supposed that it contributes to "evaporation" of the Black Hole.
Most physicist does not see "a relation of any kind" of the possible Information inside the Black Hole, and the particle
that escapes.

Here then lies the crux of the Information Loss problem (of scenario 2).
Structured matter falls into the Black Hole. However, if it should evaporate, the structured matter would be gone forever.
So, what happens to the information stored in the black hole if the black hole completely evaporates?

Some notes to consider:

Note 1: At what point does something enters the Black Hole?

Even this question is very tricky. When space gets very curved, and gravity gets immensly high, time itself
changes quickly too. It's runs slower and slower (according to "pure" General Relativity).
Although GR is not a theory of everything, the "slow" time problem needs to addressed too, before you can say
something substantial about Information Loss. And if space gets curved asymptotically, what happens with a "state"?

In a natural way, you might say that matter "enters" a Black hole at the "horizon" or the "critical Schwartzschild Radius",
as was discussed in chapter 2. However, slow time begins to have effect before that point.

Note 2: Microscopic Black Holes

Note 1:
Virtual particles is the reason why (hypothetical) microscopic Black Holes will evaporate very quickly.
Their "critical Schwartzschild Radius" is extremely small, so they do not eat. But virtual particles are everywhere,
because the Vacuum is everywhere.

Note 3: Other ways how a Black Hole might radiate?

There are other ways how a Black Hole "might" radiate:

- Quantum Tunneling effect.
- Black Body radiation.

The "Fuzzball" theory:

One interesting theory, that might resolve the "Information loss", is "Superstring" theory applied to Black Holes,
using Entropy considerations as an important tool to explore further.
It's called the "Fuzzball" theory. In effect, the theory shows that superstring and Branes can form a complex
interior of the Black hole, thereby also preserving the states of all the matter that fell into it.
The theory avoids a singularity alltogether, and thus it sounds quite promising.

See chapter 5 for more information.

The Black Hole's Surface Area:

Certain mathematics, in conjunction with clever idea's, led to the possibility that the Surface Area
of the Black Hole's horizon, might be coupled to the absorbed states of all the victimized matter sofar.
In that case, the states are probably "not lost", since the Surface Area sort of "describes" all the states.
It's an interesting idea ofcourse. However, probably just not firm enough yet, to be a leading theory in the field.

Sure, this chapter is hopelessly incomplete, but this subject is not my main mission.
So, what's the score at this point? Nobody is certain (as espected), or can really proof something.
However, the "Fuzzball Theory" seems promising.

Some articles:

Black Hole Remnants and the Information Loss Paradox (30 Jan 2015, arxiv.org)
Information Loss in Black Holes (S.W. Hawking)(2005, arxiv.org)

Chapter 5. How does Superstring Theories match up with a Black Hole? The Fuzzball?

I think that string physicists, deep into the matter, really grasp what it is about.
Ofcourse, many have a good idea, however, the math is so steep, that it prevents most of us (like me) to get the "nitty gritty" stuff.

Origininally, the (9+1) "Superstrings Theories" were unified into the (10+1) dimensional "M-Theory".

Not too long ago, a new derivative theory saw the light, namely "F-Theory", which slowly seems to have accumulated
a certain number of supporters, but I am not sure how "popular" this theory really is among string physicists.
It seems to be a (10+2) Theory, but it should not "exactly" be interpreted as having 2 time dimensions.
No doubt that all the Superstring theories are extremely "spicy" for simple mortals like me.

For about the original Stringtheories, a very short synopsys goes like so:

In Superstring Theory / M-Theory, elementary particles are "strings" on a extremely small scale.
Here, the vibrating mode of the string, determines the type of particle. This is quite a uniform statement,
and is very appealing to physicists.
There are "open" strings, and "closed" strings. The open strings are the elementary particles we know so well (quarks, leptons),
while an "entity" as the graviton (force carrier of gravity) is believed to be a closed string.

Remarkably, from mathematical requirements, M-Theory requires 11 dimensions, that is, 10 spatial dimension
and one time dimension. Since our Universe really looks like a (3+1) SpaceTime Universe (that is: 3 spatial + 1 time dimension),
the theory further states that all other extra spatial dimensions are "compactified" (or "curled up"), and thats why they
are "unnoticable" to us. The metric of those "extra" dimensions is so extremely small (10^-35 m), that effectively,
they go completely undetected indeed.

Furthermore, the concept of a "brane" was introduced, having "n" dimensions (n=0,1,2, etc..), and may be viewed as
a generalization of a "string".
However, in many papers a brane is visualized as a "manifold" or space-like object.

On later moments, it was proposed by some physicists, that not neccessarily all those extra dimensions are "curled up", or "compactified",
and that possibly one (or more) large dimension(s) exists, which are not "noticable" by ordinary open strings,
but contrary, the graviton might be "aware" of it.


As we have seen in chapter 4, a signularity Black Hole, is difficult to reconsile with information states.
Matter falls into the "black hole", while the Singularity does not change (it is a Singularity).
So, a lot of folks see a paradox here: "Information loss".

In the view of many, thus two things were not "ok": (1) the singularity itself, and (2) the paradox of "Information Loss".

5.1 The Fuzzball Black Hole:

A rather nice solution to both problems is the "Fuzzball" Black hole.

- First, it avoids a singularity, since the fuzzball is some region in space.
- Secondly, it probably cures the "Information Loss" paradox.

The Fuzzball theory was firstly published by Samir Mathur and his co workers.

Fig 2. Traditional "singularity" compared to the Fuzzball.



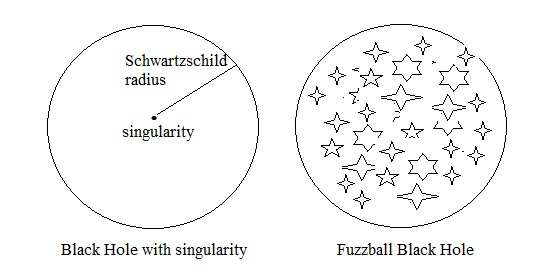
Matter might fall into the Black Hole. But here, it's not a signularity anymore. Strings accumulate or "fuse", in large numbers and density,
so that this object has all properties of our "classical" Black Hole, like the critical radius, from where the gravity
is so large, that even light cannot escape anymore.

Here are some further fundamentals of this amazing theory:

In Superstring theories, particles are strings in a (10+1) space, from which a number of spatial dimensions are compactified.
The vibration of the strings goes in all spatial dimensions.
When matter falls into the Black Hole, the new strings fuse with other strings, forming complex strings or branes.

In the formalism, it is shown that this type of Black Hole is not infinite "dense". It's quite dense ofcourse, but not extremely.

The size of the associated "critical Schwartzschild Radius", corresponds nicely with that of the classical (singularity) model,
which looks like a real plus for this theory.

The complexity of the strings/branes is supposed to conserve the "states" of the matter that was victimized into
the Black Hole. Furthermore, this horizon is not strictly defined, but is "fuzzy", meaning that interactions with fields "just outside"
the horizon might happen, which counteracts the "Information loss" problem too.
In the model, the Black Hole's "fuzzy" horizon thus radiates (some?) Information back to the Universe.

5.2 Other proposals:

Some articles:

The fuzzball proposal for black holes: an elementary review (arxiv.org)
Are Black Holes Fuzzballs? (www.spacetoday.org)
Fuzzball (string theory) (wikipedia)

Chapter 6. A note on the Planck scale and Wormholes.

Would there really exist a "wormhole-like" structure, also known as the hypothetical "SpaceTime foam",
due to large fluctuations (or Quantum Mechanical "uncertainties"), at, or around, the Planck length?

Creation of Wormholes, is often associated with negative energy, which *might* happen, if we believe
that quantum uncertainties truly exist at the smallest scales of SpaceTime.
So, from such a viewpoint, further theoretical investigations are certainly justified.
Indeed, quite recently, say the last 10 years or so, a revival took place leading to many publications.

6.1 One line of reasoning: micro Black Hole + negative energy state (from quantum fluctuations):

One nice representative (recent) scientific publication is:

Black Hole as a Wormhole Factory (arxiv.org)

Let's discuss that article, as far as I understand it...

The article is fully supporting the notion that the Planck-scale “spacetime foam”,
can be used to explain the existence of Planck-scale Wormholes.

Extremely small black holes may exist. Due to the quantum fluctuations everywhere,
negative energy states are unavoidable, and it is further assumed that such quanta entered the initial Black Hole,
as a part of the Hawking radiation process (quanta goes "in", related quanta "escapes").

Remember, when virtual particles are produced near the "critical Schwartzschild Radius", one particle may get "lost"
into the Black hole, while the other one "gets real" and escapes.
Stated in other words, but it's actually the same, is when you look at from a "quantum fluctuations" viewpoint.

The negative energy might thus result in the creation of a Wormhole throat (remember from section 1.2,
that negative energy is required for producing a wormhole).

As is further assumed with any Black Hole, Hawking radiation takes place, and in the end, a very small (micro) Black hole
might fully evaporate. However, the authors argue that radiation stops when the Black Hole's mass nears
the "Planck mass", at which point precisely, the Black Hole's Horizon matches the "throat" of the "internal" Wormhole.
What then might result, is a singularity which is shielded by the Wormhole's throat.
In upper article, mathematics is in place that support this proposition.

By the way, shielding of a Singularity in general, might be some sort of requirement of Nature.
Actually, any Black Hole (like the "large" regular ones, indeed do have a Horizon/Schwartzschild radius).

The authors then even go a step further by making it plausibe, that the micro black holes might function as
a "Wormhole Factory", since negative energy-quanta's will frequently meet the micro black hole.

6.2 Another line of reasoning: ER=EPR correspondence:

Two nice representative (recent) scientific publications are:

Splitting Spacetime and Cloning Qubits: Linking No-Go Theorems across the ER=EPR Duality (arxiv.org)
ER=EPR, GHZ, and the Consistency of Quantum Measurements (arxiv.org)

ER stands for "Einstein-Rosen" bridge (a type of intra-universe Wormhole: see section 1.2).
EPR is short for "Einstein-Podolski-Rosen" in which those three physicists published a famous article, where they
expressed doubt on the completeness of Quantum Mechanics (sort of).

EPR is also often associated with the phenomenon of "Entanglement", in which the state of 2 (or more) particles,
are intertwined in such a way, that the wavefunction (or state vector) cannot be written as a product state.
It means that you need both particles to write down the state of an observable.
It can lead to amazing measurements, if both particles are seperated (by a large distance), and a measurement
on one particle, seems to have an instanteneous effect on the outcome of a similar measurement of the other particle.
This has puzzled the scientific community for a long time, and it still does.
It was this fact that made Einstein to label it "a spooky action on a distance...

Some theoretical physicists, exploring the Planck scale, black holes, and wormholes, in the quantum foam,
proposed that Entanglement actually is due to entanglemstsc d black hole pairs at opposite ends of an ER bridge.
Those two black hole pairs are actually the endpoints of a Planck-scale quantum wormhole.

The two articles above, althoug somewhat different in the motivation, shows us a theoretical framework
to support the core claim above.

Chapter 7. Inflation and "defects" and Wormholes.

Chapter 8. The Kerr Black Hole, the Firewall model, and others.

Largely due to the movie "Interstellar", let's try to find some simple words to describe Kerr systems.