and maps to a certain output.
In math, this is ofcourse an extremely well-known concept, like for example f(x)=2x+7, or f(x)=3x2 etc..
So, for example with "f(x)=3x2", we can say that for any "x" (in it's domain), we can
find the corresponding (output) value "3x2". Thus, suppose x=3, we have the output f(x)=3*32=3*9=27.
A special class of functions in cryptography exists too. These are the hashfunctions.
They can take data of variable length, and produce output of a fixed size.
This output is often called "the hash", or "the hash value", or "the digest".
Almost always, different inputs will generate different outputs. Usually, if in an exceptional case,
two different inputs result in the same output, it's called a "collision".
However, it should be understood that "in crypto appliances" these should be extremely low or non-existent.
-If you let operate the hashfunction on some input, it produces certain output.
If you again let operate the hashfunction on that same input again, then it must produce the same output again.
In crypto language, it is often said "that if we apply the hasfunction on a fixed message,
then it always results in the same hash (or digest)."
-Generally, it is understood that a hashfunction is "one way". It's easy to get an output,
but say you have a given output, it should be practically impossible to find the associated input.
Suppose we have a simple example of a "password hash", created by the password hash function Η.
Then for example, Harry could use the readable password "MyStrongPWD", which might be mapped as:
Η(MyStrongPWD) → 045A77BBC190FFBB7CC7745
Also, suppose Mirja uses the readable password "IwantSummer", which might be mapped as:
Η(IwantSummer) → 095A76EBC140FCBA7CA3212
Note that the length of the hashes are equal.
There exists quite a few cryptographic hash functions. A few, which once were considered
to be "strong", were MD5 and SHA-0. However, around the period 2003-2009, some weaknesses
were found, and MD5 is currently not advised anymore.
Some weaknesses were found in SHA-1 too. Currently the SHA-2 and SHA-3 families, are still
considered to be very strong.
It should be understood, that if a genuine "brute force" is applied, many so-called
secure stuff, can be broken. That is, if enormous loads of CPU power is applied,
and for example runs for a year (*on average*), before a hash is cracked, you might still
consider it to be rather secure.
Indeed, it should be extremely difficult to derive the original text from a hash.
Note: some hashfunctions use variable properties in order to establish the hash,
like the system date/time, or cpu params etc..
These would not be "deterministic" (e.g. the same input must give the same output over and over),
so, in general, these are not suited for many functions in cryptography,
but ofcourse they can be useful in other applications.
Digital Signature:
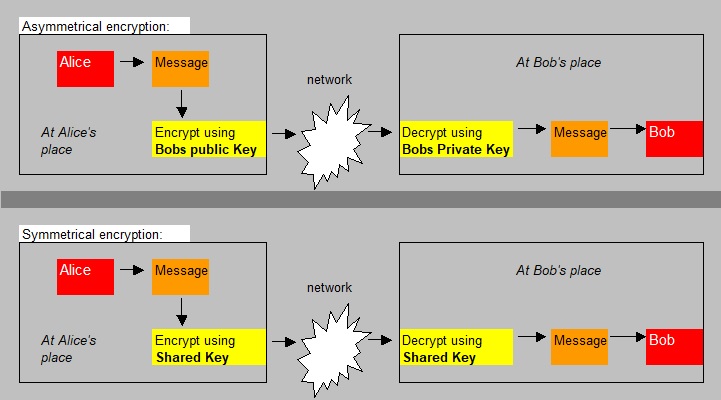
You should see this feature, as a (sort of) special case of asymmetric encription.
A Digital Signature, at creation time at the sender, uses the Private key from Asymmetric encryption,
and with verification at the recipient, the Public key of the sender is used.
The main purpose is to provide trust to a recipient, that a message is indeed from an intended sending party.
If the intended sending party, indeed already have a Private key, and a Public key to it's disposal,
then a signing algolrithm uses the properties of the message, and application of the Private Key,
"to sign" the message. The recipient then, uses the Public key of the sender to verify the signature.
3. A few words on AES, RSA, and DSA.
Let's recall this from Chapter 1:Examples of Symmetric Key implementations (thus: shared key):
AES-128, AES-192, AES-256, RC4, RC5, RC6, DES.
Examples of Asymmetric Key implementations (thus: public key/private key):
RSA, DSA, Elliptic curve techniques.
AES and RSA, are popular, and immensly important.
So what is AES?
=>General features:No, AES has never been "cracked". So, it's pretty much Ironclad.
Ofcourse, with an abnormally brute force computing power, it might in principle, be possible.
It's a symmetric scheme, so the sender and receiver must share the same key.
There are some "subtle" differences if sender and receiver are on the same machine, and
AES is implemented in hardware. However, we most often talk about a sender and receiver which
are different machines on some network. But, the AES standard, is a standard, so I do not
suggests different sorts of AES on this planet.
AES divides data into matrices of 128 bits, which you can visualize as a block of 4x4 bytes.
Now, the procedure is a complex operation of byte substitution, then shuffling of the rows,
and shuffling of the colums. Now, the procedure will do that with all those matrices.
But that's not all. Depending on the chosen key (128bit, 192bit, or 256bit keys),
a different number of "rounds" are defined, meaning that the operation described above,
will be repeated a different number of times (like 10, 12, 14).
The endresult, the encrypted data, even with AES-128, is so complex, and different from the original data,
that it might be considered "unbreakable".
Ofcourse, the more rounds are done, the more a performance hit is true, so that's why the number
of rounds is, sort of balanced, to be a number in the order of "10".
Note: the matrix size is often 128 bits. However, 64 and 256 are less common implementations too.
There are some "subtle" issues with AES ofcourse. Suppose Bob and Alice want to use AES128 for data encryption.
How do both get to know of the shared secret???
One way is the use of a PKI infrastructure, thus using the Private key/Public Key Infrastructure.
Assume that Bob is able to generate a common secret key. Say that Bob creates a message, containing a certificate,
and uses the Public key of Alice to encrypt the message.
Now, the secret key can safely be send to Alice, and she can obtain the secret key from Bob's message.
So, in this case, we have a secure channel for a short period, only to send the shared secret key.
Then, bulk encryption can take place using the secret key.
PKI is implemented in, for example, in SSL/OpenSSL, or TLS. So, usually, a user does not have to do anything.
If you have WiFi, it's interesting to see what encryption type is used. I would guess it's AES.
=> AES Block- and streams implementations:
Block cyphers (encryptors) are as we already have seen above. The data is divided in 128 bit (or 64 bit) matrices,
and each one is encrypted seperately, using the protocols as was sketched above.
AES as implemented as a block cypher, is well suited for objects like files.
I think that those are more relevant for our studies than streamed cyphers.
Streamed cyphers shuffle one byte at the time, and is more suited for streamed data.
For example, with WiFi, some time ago WEP was popular. It used a streamed encryptor with Rivest Cipher 4 (RC4).
RC4 is however practically not used anymore. Since 2013, it was suggested that it was "breakable",
and for Windows systems, Microsoft since then, advised AES instead of RC4.
A enormous amount of information was left out. As I see it today, this note is only an auxiliarlly note
in the framework of studying ransomware.
So what is RSA?
It's a Private Key/Public Key encryption type. There are a few more tastes, like Elliptic curve, or RCA.But RSA is very common.
It's not often used for bulk encryption. That's where for example AES comes in.
But it's often used to set up a secure connection, like the exchange of a certificate, or a certificate
with a shared key etc.. The protocol whih arrange that os TLS or SSL.
Once the encrypted shared key is exchanged, using PKI, then most often symmetric encryption takes over.
The Private Key and Public keys are linked by mathematics...., difficult mathematics.
The Private key remains on your system, always, and is never exposed.
It is generated locally on your PC or server, or device, and is never transmitted to anyone.
Note: It's no joke, but suppose you know something about Bitcoins (which system I do not like, sorry...),
you must be extremely carefull of the Private key, since that is the identifier which gets you to the money...
I was planning to do some math, but that is not so usefull here, as I see it now.
But the following fact is important: the generation of keys in RSA depends on
two large prime numbers p and q, and then the product N is calculated. Then some function f,
calculates (p-1)(q-1). Then the algolrithm, chooses a number "e" between 1 and that product.
Applying a modulo function on f, in such a way, that a product "d.e" exists, which exactly matches
that modulo function. Now, the entity (e,N) is the Public key, while (d,N) is the Private key.
It may come as a surprise, but the Public key is slightly earlier calculated than the Private key.
Well, at least in RSA that is true. In other schemes, it might be different.
For example, in the Elliptic curve algolrithm, the private key is first calculated, and the public one is
derived from the private key. You see? It just depends on the protocol and the associated algolrithm.
The true secret of RSA, are thus the prime numbers "p" and "q", which are critical and are never
disclosed to anyone (program, device etc..).
Those prime numbers are really large! This is why RSA is unbreakable by any practical consideration.
For RSA-2048, then two 1,024 bit prime numbers are used, and for RSA-4096, two 2,048 bit prime numbers are used.
Anyway, some info, although quite limited, on AES and RCA was shown...
As I see it now, sections 4 and 5 are not so interesting.
So, you can easily skip it.
4. Certificates.
To understand certificates, having read chapter 1 is indispensible. There, we have seen how Public and Privatekeys are used in encryption/decription.
However, in a public network, there still is an issue. How does Alice knows for sure that the shared secret key
that she received from Bob, really came from Bob?
This get's more urgent, if Bob is actually a Webshop, or financial institute, and Alice would be a customer.
In the following, let's pretend that Bob and Alice indeed have such roles.
Ofcourse, instead of a Webshop, you can substitute it by any Website that participates in transactions,
or otherwise needs secure (encrypted) datatransfer.
There are multiple types of certificates. We have "digital certificates", which is a generic term
used at all sorts of purposes. Often, people refer to SSL/TLS certificates.
SSL is actually an old protocol, and was replaced by TLS. Although many people still talk about SSL.
Most of the time, people thus actually mean the SSL/TLS certificates, when talking about "certificates".
Those are used in Internet traffic, to prove the identity of a Website, and to make encrypted datatransfer possible.
Note:
Certificates can not only be used to enable secure Internet (SSL), but also for driver signing, code signing etc..
The (SSL) certificate is a file. It thus serves two main objectives:
- The certificate is issued by a Trusted Authority (Certificate Authority), who checked the Webshop. It contains
some identifiers which uniquely identify the Webshop (like the Domain, Organization, email etc..).
Since the Trusted Authority is indeed worldwide reckognized as an "Authority", people like Alice
can trust the certificate and the organization which holds the certificate (the Webshop). - The certificate is also involved in the transfer the Public key of the Webshop, and a signature
of the Issuer, which proves the validity of the Public key.
This can be useful in a private Intranet, but it cannot be used for the Public Internet.
If, at a Webshop, a certificate is installed, that site can activate SSL which is a protocol
which sits just "above" TCPIP, and which is involved in encryption/decription.
When at a site SSL is used, the application protocol changes to HTTPS instead of HTTP,
where the "S" in HTTPS refers to "secure".
Most Operating systems, and browsers, are equipped with a list of Trusted Authorities.
⇒ Session key in Internet communication:
The certificate, and the Public key/Private key infrastructure (PKI infrastructure), does not mean that
all Internet trafic is using Asymmetric encryption, as we have seen in chapter 1.
Bulk data encryption uses a shared (common) key, often also called the "session key".
Here is what often happens in HTTPS Internet communication:
-Client connects to the Webshop.
-Webshop responds with sending it's certificate with it's signed Public key.
-Client creates a session key, encrypts it with the Webshop's Public key, and sends it to Webshop.
-Webshop decrypts it with it's private key.
-Both entities now have a shared session key, used in further encryption/decryption of data.
⇒ Certificate standard and structure:
X.509 is the standard, defining the format of public key certificates. X.509 certificates
are used in many occasions, but the application in SSL/TLS (which also makes HTTPS possible),
is widely known.
For Internet browsing and access, to verify that you are accessing the site you really intended too,
the structure of the certificate looks like the figure below:
Fig 2: Simplified illustration of the structure of a Certificate, used in an PKI infrastructure.
| Version |
| Serial number |
| Signature Algolrithm Identifier |
| Issuer Name (which provided the certificate) |
| Validity Period (Valid from, Valid to) |
| Subject Name (who requested the certificate) |
| Subject PK information |
| Issuer ID |
| Subject ID |
| Certificate Authority Signature |
-It contains Public Key information of the entity (like a Webshop) who now owns the Certificate.
-It also contains information about the Authority which issued the Certificate.
-The Issuer Name and Subject names are in the X.500 or LDAP format, thus in the form of a distinguised
name like "CN=, OU=, etc..".
-The "Certificate Authority Signature" certifies the validity of the information of the certificate,
bound to the subject (like that Webshop)
A certificate thus proves the ownership of a public key, by the named subject (like that Webshop),
listed in that certificate.
Also, the certificate contains info on the Public Key and the identity of the named subject (like that Webshop).
⇒ Trust chains:
There usually exists a "chain of certificates", or in other words, "a chain of Certificate Authorities (CA)".
Thus we have "intermediate certificates". Usually, the flow is counted from the program that uses a certificate,
all the way to the "endpoint", which is called the Root Authority, with the Root certificate.
That's why in diagrams, the Root Authority is often portraid on the utmost "right side" in the diagram.
Since we cannot go higher than the Root Authority, Root CA Certificate is always signed by the Root CA itself.
For example, the certificate issued for your Webshop, is an "end entity" certificate.
In order for a certain certificate to be used (by some device or Operating System), that certificate must have been
issued by a CA which is included in the "trusted store" of the device or program or Operating System.
So, usually all intermediate certificates must be in the store of the device or program or Operating System.
Indeed, a given Server needs all the intermediate certificates.
So, for a certificate to be trusted, it must be possible to trace it back to the trusted root,
with all certificates in the chain.
Root certificates are often packed with some Operating System already, or in a device or program,
in something often called the "trusted store".
⇒ Certificate files:
The IETF is heavily involved in Internet protocols, and thus also in describing the X.509 (certificate) protocol.
The regulations are documented in "RFC's" (requests For Comments).
Originally, X.509 was decribed by ITU, in 1988, along other X.500 specifications.
About the format, files, and purposes of certificates, a number of RFC's have been published.
If you are interested in file formats, and much more information, you might try:
rfc5280
This is certainly not a simple document (for example, for me), but it describes a lot of the "in and outs"
of certificates based on X.509.
There exists several formats of certificate files. There exists also several file extensions
of certificate files. However, there is not a one-to-one correspondence of extensions to formats.
You might see *.cer, *.pem, *.crt, *.ca-bundle, *.cer, *.p7b, *.p7s, .der, *.pfx files, and a few more.
Some of them are archives, containing a bundle of all intermediate CA's as well.
Some of them can be used to transfer a Private Key (note that typically a certificate has info on a Public Key).
How to install a certain certificate, depends on which sort of Web Server, or OS, or device etc..
you need to use it.
If you like more info on formats and extensions, you might like to see:
Various SSL/TLS Certificate File Types/Extensions
Optional reading....
5. A few words on Elliptic key encryption,
a form of "Asymmetric encryption".
This section is "optional" reading.But if you are interrested, then let's see what this remarkable stuff is about.
5.1 Elliptic curves.
For example, the Bitcoin system uses "Elliptic Curve Digital Signature Algorithm" or ECDSA, based on
Elliptic curve cryptography.
Asymmetric encryption can be used for any sort of encryption/decription in general.
What we are going to discuss here is:
-The general principles of Elliptic Curve encryption.
-A specific case, namely how a Public key is derived from a Private key in the Bitcoin system.
So, let's first take a look at the general principles of Elliptic Curve encryption.
An "elleptic curve" has a general equation y2=x3 + ax + b
Note: In math, it is shown that the real general equation has more terms than is shown above.
You know that functions (or relations) of one variable, that is, in the form of "y=f(x)" are often plot
in a two dimensional plane, having an x-axis and y-axis.
So, for example, a sketch of y=2x2 can easily be drawn, if you take the x values from say
ranging from -5 to +5, thus if x takes on the values -5,-4,-3,-2,-1,0,1,2,3,4,5, and for each of them,
calculate the corresponding y value. You then will see that y=2x2 is a parabola.
Ofcourse, here I took "x" to have integer values, but generally, this math is based on "real" numbers.
You could plot an elliptic curve too.
The Bitcoin system uses ECDSA, based on the elliptic curve y2=x3 + 7
You might wonder why this specific equation is used, and also you might wonder how a Public key
is generated using such curve. I will try to explain that in a moment.
In ECDSA, once a Private Key is established, we go to work using the elliptic curve.
That is, we use the elliptic curve, to derive the Public key.
Fig 3: Just an illustration of a particular elliptic curve.
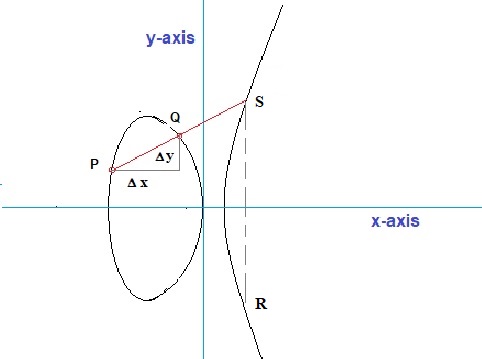
Source: my own Jip and Janneke figure.
Depending on the coefficients "a" and "b" in the relation above, the form of such curve
can vary greatly: just google on pictures of "elliptic curve", and you will see that variety.
Such a curve defines an abelian group, if the members in the group (thus the points on the curve),
adhere to a few basic rules. One of the most important rules is "closure", meaning that
an "operation" must exist, say denoted by "+", in such way, that for all members "P" and "Q",
must hold that P+Q is also member of the group (thus also a point on the curve).
It's tempting to view "+" as the addition operator, as is used in arithmetic.
Almost, but not exactly the same thing. However, in all crypto literature, or math articles
dealing on elliptic curves, the operator is indeed called "addition".
However, it is addition of any two points P and Q. For example, vector addition also
looks a tiny bit different from simple regular addition, as is used in arithmetic.
Thus the only requirement is that "adding" points, no matter how many times, must produce
again a point "somewhere" on the curve.
How would one geometrically, or algebraically, further define the exact mechanics of such an "addition"
for any members on an elliptic curve?
- Viewed from a geometrical perspective, you only have one logical option: draw a straight line through P and Q,
and see where it intersects the elliptic curve. That point then would be the "result" (apart from
from a negative sign). You cannot opt for another solution. For example, any sort of curve between P and Q would not work,
since you want one result for P+Q, and not an unknown (variable) number of other solutions.
A line is logical, but also remember that we are constructing an "addition operator", in such way,
that P+Q actually works. That is: producing a third point on the curve (member of the curve).
Viewed this way, we can say that a line through P and Q, exactly fits our "construct".
There is only one small catch. Using the principle above, we find the point "S" (see figure 3),
but ultimately we need to arrive at point "R". Here then, is a small difficulty to explain why
we must "flip" the "y-coordinate" of point S, to get the coordinates of R.
- Viewed from an algebraical perspective, you can say this:
See figure 3. You see just some randomly chosen points P and Q. I could have taken any other set,
with one exception only: when P and Q have the same "x" value, since then a line between P and Q
would go to "infinity", and never intersects the curve.
Suppose we need to express "P + Q = R" in coordinates (x,y). Here then, the aim is to find
the coordinates (x3,y3), if P and Q are expressed as (x1,y1) and (x2,y2).
But, we will introduce an intermediate step, namely finding the first true intersection "S" first, and
if that succeeds, we will immediately find the point "R", since the points R and S only differ in the sign
of the "y coordinate". Why we need to flip the y coordinate, will be explained later.
Please refer to figure 3 again. We are going to solve "P + Q = S" in terms of coordinates.
We then would have: (x1,y1) + (x2,y2) = (x3,y3)
Note that the "slope" of the line through P and Q, or in better words, the "gradient" of the line through P and Q is:
grad = (y2 - y1) / (x2 - x1) = Δ y / Δ x
Let's call this gradient "λ".
The general equation for the line between P and Q is:
y=y1 + λ (x-x1)
We need to find the intersection of that line, with the elliptic curve. So, having two unknown variables (the coordinates),
and two equations, provides us mathematically with everything needed to find the intersection S,
and thus we can find the coordinates of R too.
Both equations together, that is:
| y=y1 + λ (x-x1)
| y2=x3 + ax + b
will provide the solution for the untersection point "S". Believe me, it's just a bit of math, and nothing more.
Above is just an outline. Before we can make this more concrete, we need to return to the purpose of this excercise.
So, what is the purpose anyway? Knowing that adding points which are on an elliptic curve, must result in another point
on that curve, might be nice, but so what?
Instead of adding different points, like P and Q, we can also do "an experiment" like Q+Q.
If you look at figure 3 again, you can visualize what it means. Take a look at figure 3 again.
Now, let point P, along the curve, "crawl" towards point Q. At a certain moment, they coincide.
The line through P and Q (actually through Q and Q), is now exactly the tangent line along the curve, at the point Q.
The tangent line will intersect the curve somewhere at "T". This new point "T", is the result of "Q+Q",
except for the fact that we still need to flip the y-coordinate of T, to get the real result of "Q+Q",
but I ignore that for a moment.
You can repeat such addition over and over. You can actually try for example:
5 * Q = Q+Q+Q+Q+Q
or:
n * Q = Q+Q+...+Q (n times)
5.2. The Bitcoin Elliptic encryption "secp256k1" ECDSA Protocol.
A specific implementation of "Elliptic encryption" is used by the Bitcoin system.
That system might serve as an example of such an implementation.
-Here, the "secp256k1" SEC (Standards for Efficient Cryptography) specification is used.
This specification lists all relevant parameters for a specific elliptic curve and encryption.
-It uses the elliptic curve "y2=x3 + 7", which you can find
from the general equation "y2=x3 + ax + b" and with "a=0" and "b=7".
Fig 4: Just an illustration of the secp256k1 elliptic curve y2=x3 + 7.
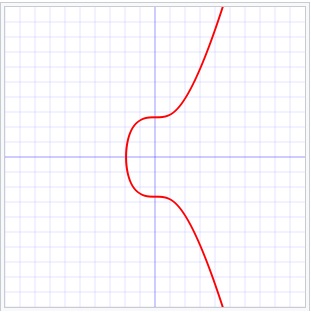
Source: Wikimedia commons (Public Domain).
-However, the x domain (the x-axis) is not the familiar set of (continues) real numbers, but a discrete set
of numbers for which the specification is set in "secp256k1".
Using this set of "x values", produces a discontinue scatter diagram (not shown in this note).
-A base point on "the curve" is defined, rather randomly, but once chosen, it is fixed.
Usually, this base point (or reference point) is denoted by "G", but other letters are found
in the literature too.
Ofcourse, since we have now a discrete set of x-values, we cannot actually speak of "a curve",
but "G" is indeed an element on the scatter diagram, quite similar as if we still would have
used a continues curve.
-Using the analogy of a continues curve, just like above, we are able to perform a calculation
like:
5 * G = G+G+G+G+G
or:
n * G = G+G+...+G (n times)
-Likewise, a Public key can be derived using such system, using the equation:
Kpublic = kprivate * G
Where kprivate is a 256 bit number.Note that the equation above, is not much different from an equation as "n * G = G+G+...+G (n times)".
It's a one-way system. It is commonly believed that it is not practically possible
to calculate the Private Key, from such Public Key.