Contrary, now you are able to analyze a (much) smaller "sample" out of the whole Population.
Indeed. Most often, you are only able to study a "sample" from the the whole population.
If you want to "measure" the opinion of millions of people in a country,
then usually, you are not able to interview all of them. So, you try to get a representative "sample"
from the whole population.
Intrinsincally, you introduce "uncertainty".
Indeed, a core difference between "Population statistics" and "Inferential statistics",
is that the latter intrinsically deals with a certain level of uncertainty. We simply cannot
measure or observe the whole Population. We need to deal with a representative sample only.
Contrary, "Population statistics" is exact.
If the number of data elements you measure ("n"), gets larger and larger, then the difference between
"Population" mean and Standard deviation, compared to "Sample" mean and "Sample" Standard deviation,
will more and more narrow down (theoretically).
In population statistics (chapter 1), it is argued that if you can access or "see" all data, that is "N" events or "N" values,
then ofcourse you can calculate the "exact" mean μ and the "exact" standard deviation σ.
It is then rather logical to use "N" as the value of the denominator. You simply have N values.
Here I repeat equations (1) an (2) again:
| mean value μ = | a1 + a2 + ...+ aN -------------------------- N |
= | 1 --- N |
Σ ai (equation 1) |
| σ = | √ | ( | 1 --- N |
Σ (ai - μ)2 | ) (equation 2) |
Note that "N" is the number of elements in the population.
Also note that μ and σ, are the (more or less) "official" symbols for the population mean
and standard deviation repectively.
In a way, you might say that we are not really doing "statistics" here. Why? We just have "N" values,
and we are, for example, able to calculate μ exactly.
It's in reality more typical that we can only analyze a "sample" from the Population.
Here, a sample consists of a number of observations from the population, but that number is
typically much smaller compared to the population as a whole.
The equations to obtain the socalled "Sample" mean and "Sample" Standard deviation, look very similar,
but for the "sample" Standard deviation, there is a small difference.
So, suppose you have found, or measured, "n" (bi .. bn) values (from a much larger Population),
then the "sample" mean value x̄ and the "sample" standard deviation "s", are:
| x̄ = | 1 -- n |
Σ bi (equation 3) |
| s = | √ | ( | 1 --- n-1 |
Σ (bi - x̄)2 | ) (equation 4) |
or
| s = | √ | ( | 1 - n |
Σ (bi - x̄)2 | ) (equation 4") |
Why do we devide by "(n-1)" in equation 4, instead of just "n" at equation 4"?
There exists arguments that consider the "degrees of freedom" comparing "population-" and "sample"
deviations. Anyway, the (n-1) is called "Bessel's" correction for bias.
While we are considering only "n" values from a much larger population, there is a serious risk
of a certain (low?) amount of bias.
If we calculate "s" using a division by (n-1), then "s" is larger than just by deviding by "n".
This might be what we want. A larger "s" means simply a somewhat larger deviation, which is really true,
since you can only have a smaller deviation by considering the whole population.
So, here we have a "reasonable construct". Deviding by (n-1) increases "s" somewhat (compared by
devision by "n"), thus increasing "s" somewhat, on purpose.
As a simple example, "10/(6-1)" = "10/5" = 2, is larger than "10/6" = (about) 1.66.
Indeed, a larger (or wider) sample standard distribution, designates that we can expect (somewhat) more spreading
around the mean value.
It's a bit philosophical whether to use a division by "n" or "n-1". However, most folks ignore "Bessel's" correction,
and thus simply use "n" in the formula of the standard deviation (equation 4").
Indeed, some folks are "pro", but others are "contra", in using Bessel's correction.
If you are in any doubt in a certain situation, then simply use "n" instead of "n-1".
But do not be surprised, if in some textbooks or articles, "n-1" is used.
Note that "x̄" (x bar) and "s", are the (more or less) "official" symbols for the "sample" mean
and "sample" standard deviation repectively. But that's not too strickt too, and other symbols might
be used in some articles or textbooks.
Chapter 3. Average, standard deviation, and Frequency distributions for "grouped data"
In Chapter 1, I often simply used a series of values (a bunch of numbers) in my examples, and illustrated the calculationof the average, median, or standard deviation.
That's all well ofcourse, but in many cases, the approach is a little different.
Most often "equal spaced" intervals (or "classes") are used, and then we count how many events fall
in each interval.
Then, when all events (or observations) have been grouped into different classes, we can calculate
the mean and standard deviation again.
But, those key values as average, and standard deviation, then must be obtained using a slightly
different approach (compared to chapters 1 and 2).
This approach is often used in "Inferential statistics". With "Population statistics", all elements
can be accessed, and thus is the construction of Intervals, or classes, not much useful.
It can be done ofcourse, but it is not much useful. This will be explained below.
It may seem strange, but the symbols often used, are those of Descriptive-, or Population statistics,
that is: μ (the mean) and σ (the standard deviation).
But, in many books or articles, we may also find the usage of x̄ (the "sample" mean) and
"s" (the "sample" standard deviation).
Do not worry too much about symbols anyway.
3.1 Histograms, and Distributions.
"Frequency Distributions" are quite simple to illustrate. Let's try an example.Example:
Suppose you want to know how many people vote "left", with repect to their age.
Then you could use "equi spaced" intervals, like the age in 20y-24y, age in 25y-29y, age in 30y-34y, etc...
Then, for each such interval, you phone (or try to contact) 1000 people, and ask what they are going to vote for.
What you might get is something like counting 30 votes in 20y-24y, 60 votes in 25y-29y, .., etc...
You might then create a "Histogram", where on the "x-axis" (horizontal axis), you place your intervals,
and on the "y-axis" (vertical axis), you mark the counts for each interval.
The "equal spaced" intervals, are sometimes also called "classes" or "class intervals".
For example, the class 20y-24y, has two "class limits" (20, 24), and a "class mark", which is the middle number
in that class (22). And it has a "class width" of 5, as all other classes have.
In our example, we might have found the values (counts) for each class, as illustrated in figure 1.
The figure is called a "frequency distribution", and the type of graph choosen here, called is a "histogram".
Figure 1. A frequency distribution, displayed in a "histogram".
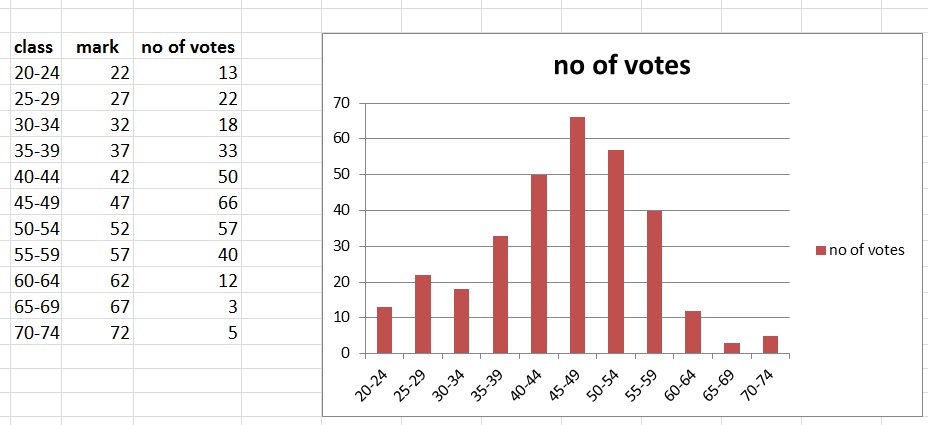
You might ask: How would you address the "mean value" and standard deviation in such an frequency distribution?
That would be a very good question. We are going to discuss that in section 2.2.
3.2 The average and standard deviation for "grouped" data, in classes.
In the example above, I used the term "number of votes". But actually, it's the frequency,or the number of counts, per class.
When calculating something like the mean value, we need to have to take into account the number of counts,
that is, the frequency.
This is a difference with chapter 1.
Essentially, in chapter 1, we had a bunch of numbers, where each of them, had a frequency of "1".
When viewed from that perspective, you might already understand right away, that we now must multiply
each class "midpoint", with the frequency in that class.
Here are the equations for the mean value and standard deviation. I will illustrate thus further in the example below.
Determining the mean value for grouped data in classes:
| μ = | Σ fi mi -------- (equation 5) Σ fi |
where "Σ fi" in the denominator, is the sum of all frequencies. This is the "sort of" equivalent
to the "N" of equation 1.
or, as an equivalent equation:
| μ = | Σ fi mi ------- (equation 6) N |
Where:
N: is sum of all frequencies (Σ fi)
mi: is the midpoint (or class mark) of each class
fi: stands for the frequency of each class
Determining the Standard Deviation for grouped data in classes:
| σ = | √ | ( | 1 --- N |
Σ fi (mi - μ)2 | ) (equation 7) |
Since this all is about a "sample" from a larger "population", you might say that
we have to use "1/N-1" in equation 7 above.
That's right. But many folks simply avoid the (N-1), and use "N" instead.
Using (N-1) is called Bessel's correction, and that is not without some controversion.
But don't forget that statistics over "samples" has an intrinsic uncertainty anyway.
So, in a rather "formal" way: yes, use "1/N-1".
But, if in some articles or textbooks etc.., you see that "1/N" is used for the standard deviation,
then let's not panic. Using simply "N" is defendable, using good arguments.
We will illustrate the calculation of μ and σ in the example below.
Example determining μ and σ :
Here I will use only 4 "classes" (or 4 intervals), to keep the length of the calculations limited.
You can make a class rather wide, or rather small, as is applicable for a certain situation. A class is supposed
to contain adjacent values, thus like an interval as [10-14], meaning 10, 11, 12, 12, 14.
Note: Actually, there exist recommendations on how to divide a certain range into classes.
One important point is: we collect all "counts", for all members in the class (like 10, 11, 12, 12, 14),
into one number. This sum of counts, is actually the frequency for that class.
This one number is the "midpoint" (average) in that class.
Suppose we have found the following frequencies (counts) for the following classes:
| Class: | Freq. or counts: |
| 10-14 | 3 |
| 15-19 | 8 |
| 20-24 | 6 |
| 25-29 | 1 |
Next, let's determine the local average per class, that is mi, or the midpoint for that class.
And, then we multiply the "local average" with the frequency for that class, that is, fi * mi:
| Class: | Freq. or counts: | Midpoint: | Midpoint x Freq. |
| 10-14 | 3 | 12 | 36 |
| 15-19 | 8 | 17 | 136 |
| 20-24 | 6 | 22 | 132 |
| 25-29 | 1 | 27 | 27 |
Here, the total number of counts "N", or the sum of all frequencies "Σ fi" is 18.
We are now able to calculate μ and σ.
Using equation 3, the mean value μ is:
Determining the mean value for grouped data in classes:
| μ = | Σ fi mi -------- Σ fi |
= | 331 ---- 18 |
= 18.4 |
A mean value "μ" of 18.4 for values that range from 10 to 29, seems in order, also taken the frequencies
into account.
So, we succeeded in calculating the mean value, for grouped data in classes.
Maybe you like to calculate the standard deviation yourself.
In Chapter 6, we will see some important distributions, namely the "Gaussian" (or "Bell"-, or "Normal" distribution),
the "binomial" distribution, and the "Poisson" distribution.
Chapter 4. Some key elements from Combinatorics and "Sets".
This will be a relatively short chapter, since I only want you to understand what n! means,and how we must interpret something like "n over k" or (n!/(n-k)! k!)
After that, we need to know a few basic terms and concepts associated with sets and collections.
4.1 Permutations of "n" elements, and the notion of n!:
4.1.1 Permutations Without repetitions:
⇒ First, let's do an Example With Repetitions:Suppose you have 2 basic elements, like "A" and "B".
Suppose further you must create "sets" of 9 elements, like "AABAABBBA" etc.., where repetitions
of "A" and "B" are allowed.
Question: How many different sets can you build?
First, it's important to realize that we may use repetitions here, like "AABAABBBA", or "BBBBBBBBA" etc..
It's fully similar to "bitstrings". If you have "0" and "1", how many different sets can you build with a length of 3?
The full set is:
000
001
010
011
100
101
110
111
So, here the answer is 8. Note that this is equal to 23.
It turns out, that if you have "n" different elements, and you must create sets with a length of "k",
where repetitions are allowed, the answer is:
number of different sets (with repetitions) = nk
If we return to our example of sets" of 9 elements, with the elements "A" and "B", then:-n=2
-length=9
-repetions are allowed
So, the answer is 29=512.
⇒ How must we interpret an expression as n ! (n with an exclamation mark)
Suppose we have some discrete set of "n" unique elements.
This could be a set of numbers like {1,2,3,4}, or, in general, the set of numbers {a1, a2, .. ,an},
or a set of coloured balls {red, blue, green, yellow, purple) etc..
Suppose we have the set {A,B,C}.
A key question is: how many different unique arrangements, without repetitions, can we create out of that set?
Folks also rephrase that as: How many Permutations without Repetition can we create out of that set?
In such a permutation, the ordening of the elements is most important.
Note that:
-An ordering as for example "AAB" is not allowed, since we require "without repetitions".
-The arrangement as for example ABC is different from CBA, since they are ordered differently.
You can use plain and simple logic here. For the first element, we can choose from 3 elements. Then, for the second element,
we can choose from 2 elements (thus one less), and for the third element, we can only choose one (thus 2 less).
No matter with which element you start with, the above reasoning will always hold.
Let's work out our simple example. We can only create the unique arrangements:
A B C
A C B
B A C
B C A
C A B
C B A
So we have 6 unique arrangements (Permutations without Repetition).
You can try to find more, but it will not work.
Note that in this case : Permutations without Repetition = 3 x 2 x 1 =6
Mathematicians often use "induction" to proof a general statement. Then they say that if the statement holds for "n",
then let's see if it also holds for "n+1". Since "n" is just arbitrary, and it works out, the theorem is proved.
I only go for "make it plausible", which is justified for speedy intro's in math.
What we have seen above, holds for the general case too.
If we have "n" elements, the number of unique orders (Permutations without Repetition) = n x (n-1) x (n-2) x .. x 2 x 1
Now, n! is defined as:
n! = n x (n-1) x (n-2) x .. x 2 x 1 (equation 8)
And this also corresponds to the number of unique orders (Permutations without Repetition).Number of permutations of n elements, no repetitions = n! (equation 9)
Some examples:2! = 2 x 1 = 2
4! = 4 x 3 x 2 x 1 = 24
10! = 3628800
Furthermore, 0! is defined to be "0". Note further that n! is defined for positive integers only.
Some other characteristics of "n!":
Suppose we have the (positive integer) number "k". Then we can calculate k!
But also note that k! = k x (k-1)!
Example:
5! = 5x4x3x2x1
5! = 5x4! = 5 x 4x3x2x1
4.1.2 Permutations With repetitions:
We already have seen an example in section 4.1.1 above (first part).You can use plain and simple logic here too. For the first element, we can choose from "n" elements. Then, for the second element,
we can choose again from "n" elements etc.. etc..
So without proof, we say:
Number of "r" permutations of "n" elements, with repetitions = n x n ...x n (r times) = nr (equation 10)
Here, we have "n" elements to choose from, and we do that "r" times.For the example of section 4.1.1, where we have the letters A, B, and C,
the number of permutations with repetitions would then be 33 = 27.
4.1.3 Permutations, Combinations, Variations?:
When you study different articles or textbooks, you might find some subtle differences in the meaningof permutations, combinations, and variations, especially the latter two.
Above, in section 4.1, we described "permutations".
I would like you to keep in mind that, mathematically, it is said that:
With permutations, the order of the elements does matter.
With combinations, the order of the elements does not matter.
So, from the example in section 4.1, we would say: in a combination, those 6 arrangements are all the same !
Indeed, it would be "1".
That's also why the number of combinations is most often viewed in the context of "taking k elements from n elements".
It works a bit counter-intuitive, since the concept of "combination" in daily usage, seems different.
For example, if you have a "combination lock" of 3 digits (where each digit is a number in [0-9]), then
we would say, in daily usage, that all arrangements from 000 up to 999 are combinations.
So, we have 1000 possible combinations, like "101" or "222", or "555", or "937", etc...
This is not the general interpretation in math.
Here is an example of the number of combinations, in the context of "taking k elements from n elements".
Suppose we have the set {A,B,C}.
Which number of combinations of two elements can we derive of the set above?
It's:
AB
AC
BC
Remember, that with "combinations", the order of the elements does not matter.
Thus, for example, AB and BA are then actually the same thing. So, we only "count" one of them.
4.2 Combinations of "k" elements, from a larger set of "n" elements:
Remember, when finding "combinations" the order of elements does not matter.Using "induction", it's not too hard to prove the theorem below. However, considering the "weight"
of my notes, making something "plausible" is often sufficient.
In section 4.1.3, we used the example of finding the number of combinations of two elements from {A,B,C}.
So, in this particulaar case, the total number of elements "n", is 3,
while we want the number of combinations of "k" elements, which is 2.
We found:
AB
AC
BC
Remember, that with "combinations", the order of the elements does not matter.
Thus, for example, AB and BA are then actually the same thing. So, we only "count" one of them.
Using that same example, the number of combinations is calculated as:
| number of combinations = |
n! ------- k!(n-k)! |
= |
3! ------- 2!(3-2)! |
= |
6 -- = 3 2 |
In this particular case, the formula works out.
You can check out some other examples yourself. You can use numbers, letters, coloured balls, or names etc..
Indeed, the equation works in general as well for the number of combinations of "k" elements from "n" elements.
Above we alreadyy have seen the general equation. However, for that equation also a special notation
is used (just a definition). It's pronounced as "n choose k", or sometimes "n over k":
| number of combinations of k out of n = |
┌ n ┐ └ k ┘ |
= |
n! ------- (equation 11) k!(n-k)! |
Remember, that the calculation is done using:
|
n! ------- k!(n-k)! |
While
|
┌ n ┐ └ k ┘ |
is just another way to notate that calculation.
4.3 Permutations of "k" elements, from a larger set of "n" elements:
The number of combinations (from k out of n), generally is smaller than the number of permutations.With permutations, the order does matter, so for example "BA" is different from "AB",
while with combinations, "BA" and "AB" are simply counted as "one".
| number of permutations of k out of n | = |
n! ----- (equation 12) (n-k)! |
Suppose we have the set {A,B,C} again.
How many different Permutations, of 2 elements out of 3, can we create out of that set?
(ordering matters, and no repetitions of elements).
So, here "k"=2 and "n" =3. Using equation 12, this will yield:
|
3! ----- (3-2)! |
= |
3 x 2 x 1 ---------- 1 |
= 6 |
If we just write it out, we get:
AB
BA
AC
CA
BC
CB
So indeed, 6 is the answer.
4.4 A few notes on sets.
If you have different "sets" (or "coillections") of objects (like numbers, coloured balls etc...),you can perform several "set operations". Here, we take a quick look at the most important ones.
Figure 2. Venn diagrams of some sets.
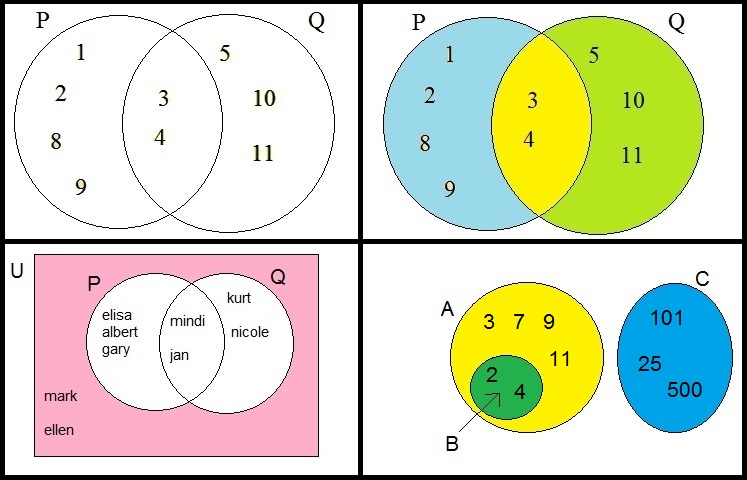
In figure 2 above, you see a few socalled "venn" diagrams, which helps explaining the "Union"
and "Intersection" of sets.
Suppose that P is the set {1,2,3,4,8,9}
You see that represented in figure 2, in the first quadrant, by a circle containing those elements.
Suppose that Q is the set {3,4,5,10,11}
You see that represented in figure 2, in the first quadrant too, by a second circle containing those elements.
- The Intersection of sets:
Now we might wonder: which elements do have "P" and "Q" in common?
From figure 2, it is obvious that these are the elements "3" and "4".
Those common elements are called the Intersection of the sets "P" and "Q".
It's notated in this way (using the example in figure 2), using the "⋂" symbol:
P ⋂ Q = {3,4}
In figure 2, the second quadrant, I represented the "Intersection" as the common (overlapped)yellow area of the two circles.
- The Union of sets:
We can also "add" sets, or stated in "set theory" language, "join" sets or "union" sets.
In our example of P and Q above, the union would be {1,2,3,4,5,8,9,10,11}.
It's notated in this way (using the example in figure 2), using the "⋃" symbol:
P ⋃ Q = {1,2,3,4,5,8,9,10,11}
In figure 2, the second quadrant, I represented the "Union" as the combination ofboth two circles (blue, yellow, and green area's).
Note: why don't we count an element like "3" double, that is, two times?
The elements themselves are fundamental. You can "draw" any closed line between any
number of elements, and thereby "declaring" a set.
This way, you might have multiple sets containing the same element. But not the elements themselves
will double magically. So, in Intersections or Unions we will count them one time.
- The complementary of a set, like Ā or AC :
If we look at the example set P and Q again, and suppose we want to list
all elements which are not element of (or do not belong to) P, then in figure 2 (second quadrant),
it would be the green area, that is the elements {5,10,11}.
In general, if you have set "U", then the complementary set is often denoted by "UC", or "Ū".
- Subsets:
In the fourth quadrant of figure 2, you see the sets A, B and C.
We can see that A, B, and C contain:
A={2,3,4,7,9,11}
B={2,4}
C={101,25,500}
It's crucial to note that the elements 2 and 4 belong to the set A as well.
Indeed, the circle representing A, contains all those elements as listed below.
By coincidence, B contains 2 and 4 as well (actually only 2 and 4).
As you might already have guessed, is the fact that B is a subset of A.
In contrast, if you take a look at P and Q again: in that case we do not have the situation
that either one is a full part of the other one.
In "set theory" language, if B is a subset of A, it is notated as:
B ⊂ A
- The Empty set ∅As the last remark of this section, I like to attend you on the fact that set A is fully disconnected from set C.
They do no have any element in common. Their "intersection" is "empty", often denoted by the symbol "∅".
So, if sets do not have any intersection, we say that:
A ⋂ C = {∅}
Ok, now let's finally move on to "Probability calculus".Chapter 5. Probability calculus.
When the subject is about "probability theory", usually, people speak of "events", and each of such an eventhas a certain number of possible "outcomes", where each outcome has a certain "probability" to occur.
Actually, there are two main "forks" here:
1. The more "mundane" probability theory on a finite, and discrete number of possible outcomes of an experiment.
What I call "experiment" here, could be for example, the throwing of a dice, or drawing a card from a deck of cards,
or grabbing a ball from a large box with many differently coloured balls, or tossing a coin, etc.. etc..
Note that the "space" of all possible outcomes, is limited and contains discrete outcomes.
This collection of all possible outcomes is often also called sample space.
This is the subject of section 5.1.
2. We can also deal with a continuous stochastic variable.
This sounds more complex than it actually is. It simply means that the "space" of all possible outcomes, is continuous
and is "uncountable". For example, the position of a particle in space. In Quantum Mechanics, we may only speak of the
probability that a particle is in some region of space.
As another example, if you would measure the length of a very large group of people, the distrubution of the lengths
varies so much, that we may treat it as a continuous "variable".
This is the subject of section 5.2.
5.1 Probability theory of a discrete outcome space (sample space).
5.1.1 General Probability definition (Laplace).
As a simple but effective example: you can throw a dice (an event), and if you throw a six, then that is a certain outcome.Ofcourse, in this case, there are 6 equivalent outcomes, which we can decribe with the set {1,2,3,4,5,6}.
In this example, we don't have to be like Einstein to formulate the "probability" of any of those outcomes.
Using plain logic: each number has a "one out of six" chance to occur.
So, for example, the probability of throwing a "3" (or any other face of the dice) is:
| P(outcome=3) = | 1 -- 6 |
For similar events, a "general equation" can be formulated. If there are Nf favourable outcomes
for a certain result "f", out of a total number of NT outcomes, then the probability of finding "f" is:
| P(f) = | Nf -- (equation 13) NT |
Example:
The probability of drawing an "ace" from a deck of cards is:
| P(ace) = | 4 -- 52 |
Indeed, since there are 4 aces in the deck of 52 cards, the probability of finding some ace, must be 4/52.
Although we have not proven anything, here, all of the above calculations are simply based on "common sense".
Here are some other rather "logical" (but very important) theorems:
5.1.2 Some Theorems (without proof), and illustrative examples:
(1): Total of All Probabilities:
Consider an event with N possible (discrete) independent outcomes. Suppose that for outcome "i", the probabilityis denoted by "Pi", then:
The Sum of all probabilities = Σ i=1i=N Pi = 1 (equation 14)
As you know from former notes, the Σ is a shortcut notation for a summation of all Pi, where i runs from 1 to N.Thus, for example, if you throw a dice, the total probability of throwing a 1, or 2, or 3, or 4
or 5, or 6, is "1". In other words, the probability of throwing whatever number, is "1".
So, you can sum up all individual probabilities and the full total just have to be "1".
(2): Complements rule:
It's universally true that:If the probability on outcome "A" is P(A), then P(Not A) = 1 - P(A) (equation 15)
Example:Suppose you draw one card only, from a deck of cards.
Then the probability of drawing the "ace of spades", is 1/52.
So, finding NOT the ace of spades, is 1 - 1/52 = 52/52 - 1/52 = 51/52.
Example:
If you throw a dice once, then the probability of getting a "3" or "4" is: 1/6 + 1/6 = 2/6 = 1/3.
So, the probability of NOT getting a "3" or "4" is: 1 - 1/3 = 2/3.
(3): Adding probabilities:
This subject is not difficult, but it needs some "subtle" considerations.The question is: how "much overlapping" exists between the event spaces (sample spaces), for which we want to
"add" the probabilities.
As you will see in a moment, not always can we simple add the individual probabilities "just like that".
We better view this from "set theory".
Case 1:
Suppose you (randomly) select an element from set A, and (randomly) select an element from set B.
Now if the intersection of A and B is empty or {∅}, then A and B have absolutely nothing in common.
The addition of probabilities is expressed in set language too. In this case, an event that applies to A
and an event that applies to B, is written as:
P(A ⋃ B) = P(A) + P(B) (equation 16)
So, here we have a "pure" addition.Case 2:
Again, suppose you (randomly) select an element from set A, and (randomly) select an element from set B.
Now if the intersection of A and B is NOT empty or {∅}, then A and B have elements in common.
To avoid "double counting" we must then "subtract" the intersection from the Sum of probabilities:
P(A ⋃ B) = P(A) + P(B) - P (A ⋂ B) (equation 17)
Example of case 2:Suppose you draw one card of a deck of cards.
What is the probability that this card is a "spade" or an "ace"?
There is an overlap between the set of all spades, and the set of all aces.
In other words: there exists an intersection between the set of all spades, and the set of all aces.
Namely, the card ace of spades.
Indeed, it's not always easy to take the right choice between using equation 15 or equation 16.
In this case, we were able to identify the intersection between the sets, so we must use equation 16.
So:
P(spades ⋃ ace) = P(spades) + P(ace) - P (spades ⋂ ace) = 13/52 + 4/52 - 1/52 = 16/52.
(4): Multiplying probabilities:
Again, there are several intracies here.A proper treatment would go into the subject of "conditional" probabilities.
However, I will only touch the simplest case: when two (or more) events are completely independent.
If that is indeed so, you generally must multiply the individual probabilities of the events.
Example:
You toss a coin one time, and then throw a dice one time.
What is the probability of obtaining "tail" AND throwing a "3"?
These events are completely independent (let's not get philosophical).
So:
P(tail AND 3) = 1/2 x 1/6 = 1/12
Example:
You throw 2 times in row with a dice. What is the probability of throwing a "2" first, and a "3" the second time?
Again, these events are completely independent (let's not get philosophical).
So:
P("2" AND "3") = 1/6 x 1/6 = 1/36
It's sometimes not easy to decide if you must add probabilities like
in equations 15 or 16, or when you must multiply probabilities.
For what it's worth: Here is Albert's tip (not full proof):
-When in English you read: "event A" OR "event B": you probably (no pun intended) must add probabilities.
-When in English you read: "event A" AND "event B": you probably (no pun intended) must multiply probabilities.
5.1.3 The "Binomial Probability" equation.
Example:If we throw a dice 3 times, we know how to calculate the probability to throw a "2" first, then a "5",
and then a "6". These are three independent "events", so we must multiply probabilities.
It will be this: P(2,5,6) = 1/6 x 1/6 x 1/6.
Now consider this: what is the probability to throw a "6" first, then a "6" again, then lastly, "NOT a 6"?
I suppose the answer is this: P(6,6,NOT 6) = 1/6 x 1/6 x 5/6.
Now take care: Suppose we call "p" the probability to throw a 6. Then throwing "NOT a 6" is "(1-p)".
Let's call (1-p)=q.
So, we can rewrite the probability above as: P(6,6,NOT 6) = p x p x (1-p) = p2 x q.
Now, let's turn our attention to the "Binomial Probability" equation.
It's not unlike we have seen above. If we are dealing with "n" independent experiments (or events) where at each
event we can obtain "success/failure" or, equivalently, "yes/no", or whatever else two distinctive outcomes,
then the probability to find "k" successes in "n" experiments (or trials) is:
| P(k) = |
┌ n ┐ └ k ┘ |
pk (1-p)n-k (equation 18) |
Here, "p" is the probability to find "success" (or "yes", or other sort of twofold outcomes),
and (1-p) is the probability of "failure" (or "no", or other sort of twofold outcomes).
It's possible to proof equation 18, but I will only make it "plausible" here.
The term "pk (1-p)n-k" is actually not different then an extension of the example we saw above.
But why the "n choose k" term?
Well, we only ask for "k" successes out of "n" attempts.
Remember section 4.2? That section is titled "Combinations of "k" elements, from a larger set of "n" elements".
There we found that we can have "k" elements (successes) out of "n" elements (attempts), but there exists
a variety of the k's along the n's. For example, we can have "yyynnyynnnnnyy" with 7 "y's", but this one
"ynnnnyynnyynyy" has 7 "y's" too, so there are multiple Combinations of "k" elements, from a larger set of "n" elements.
So indeed, we have to multiply the factor "pk (1-p)n-k" with the "n choose k" term as well,
in order to find all combinations for which "pk (1-p)n-k" is true.
Example:
Suppose we have 10 marbles, 4 are red and 6 are white. We randomly, pick a marble, see what colour it is,
and place it back. We do three experiments in the same way, in total.
We are looking for the probability of selecting red marbles.
Now, you need to determine what is exaxtly the "stochast" X here. Namely, you can find 0, or 1, or 2, or 3, red marbles.
So, for example, we may express the probability like for example "P(finding two reds) = P(X=2)".
So, the variable X here, is the found number of red marbles.
Now, remember that you are doing 3 experiments here. You might think that n=10 here, since the number of marbles is 10.
Not so! You are doing 3 experiments, each of which can be a succes or failure. So, n=3.
So:
| P(X=2) = |
┌ 3 ┐ └ 2 ┘ |
0.42 0.61 | = (about) 0.29 |
Often, the difficulty is not so much the calculation, but determining what represents "n" and "k".
5.1.4 The "Conditional Probability".
Suppose we want to calculate the Probability that "event1" has as outcome "A",while we require that "event2" has as outcome "B" (beforehand).
There is something remarkable here. We MUST have that "event2" has as outcome "B",
which then likely is to restrict the possible outcomes of "event1".
That such a restriction for event1 exists, is most often true. The possible outcomes for event1,
are likely to be limited, since we require that "event2" has "B", instead of no requirements at all.
We write this as: P(A|B).
Ofcourse, when we have two completely seperate physical events, not correlated in any way,
then we do not have a realistic conditional requirement.
However, that's exactly the hard part in some circumstances. That is, to determine if
two event can have any "influence", or not any "influence", on each other.
Example:
Question: What is the probability that we draw a "spade" from a deck of cards, under the requirement
that we must have an "ace".
The answer might surprise you.
-Wrong answer:
Well, we must have a "spade" and it must be an "ace" (that's the requirement), and
that's only one card out of 52 cards, so P=1/52.
-Better answer:
The requirement is that we must have an "ace". So, considering all aces, you will see that
you only have 4 different aces in the whole deck. So, we are limited by 4 aces.
That's the requirement.
Now, to draw the "ace of spades", is only one possibility out of 4 possibilities, so P=1/4.
It is just as if the whole outcomespace of event1, is projected to a subset, due to
the requirement of event2.
The answer above, is what folks from probability theories likely want you answer
for the question in Example 1.
From a philosophical prespective, you might still have some questions.
Anyway, what we have seen above, is how the math is done.
-You might view the whole matter this way: in what way, does the "requirement" (B),
limits the possible outcome space of A?
or
-We know that requirement B is in effect beforehand. So, this limits the possibilities of A.
In a general formula, we have for the conditional probability:
| P(A|B) = | P(A ⋂ B) ---------- P(B) |
I personnally, understand the relation above, much better if it's rewritten in this way:
P(A ⋂ B) = P("intersection of the events") = P(A|B) * P(B)
5.2 Probability theory of continuous stochastic variable (sample space).
Ok, this is the last section of this very simple note.Al of the above, dealt with a "discete" outcome space. However, in many occasions we have
a (nearly) continuous "outcome space".
-For example, the times when vistors enter a store.
-Or, the position of a particle on the x-axis (in 1 dim space). This might be considered to be really "continuous".
-Or, the length measured of 500000 people at the age of 30y.
In this case, the number of measurements is so large, that we may treat it as a continuous "variable".
Plotted in a XY graph, most measurements will be in the interval 140cm - 190cm, while the graph probably
will quickly lower at x > 190cm and x < 140cm.
Example:
Or, what about the lifetime of a lightbulb? Theoretically, the lifespan will be in the interval [0,∞],
but for a certain type, you might find a mean value of, say, 6 months.
Suppose you did an incredably large number of measurements. In a graph, you might find something like shown in figure 3:
Figure 3. lifetime of lightbulbs.
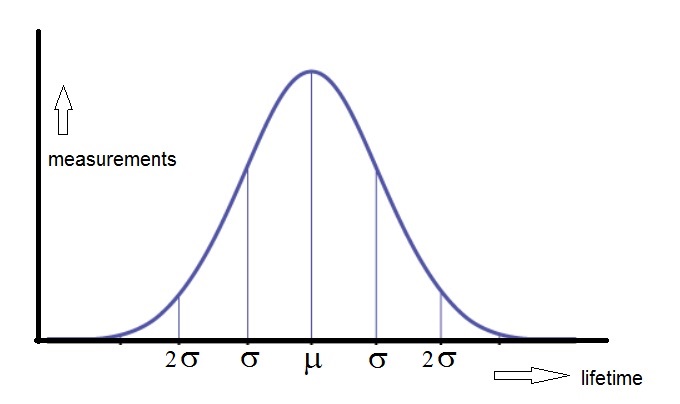
Most lightbulbs will obviously function with a lifespan near a certain mean value μ.
However, some will function for a very long time, much longer than μ, and ofcourse some
will function for a much shorter time.
This is all expressed in the example of figure 3. With graphs, usually, we talk about an "x-axis" and "y-axis".
But those are just names or conventions. In figure 3, we have the "livespan" having the role of "x",
and "number of measurements" having the role of "y".
Note that this particular figure is symmetrical around μ.
In case of a continuous stochastic variable, we have no other choice than to use a "probability function f(x)",
or more often called a "probability distribution".
When we see that in a graph, we see a continuous function in a XY coordinate system, where the "outcomes"
are on the x-axis, and the "frequency" is on the y-axis.
In former notes we already have seen that a definite integral is actually an infinite sum, where the
discreteness of the "intervals" goes to zero. See for example note 14.
We have a similar case here too.
Since the "total" probability must "add" up to "1", we have to use an definite integral over the full range of "x".
- Suppose that a "probability distribution" is completely defined over the interval x in [a,b], then:
∫ab f(x) dx = 1
Note that the sum (or integral) of the total probability corresponds to the "area" of the region boundedby f(x) and the x-axis, over [a,b].
- Suppose that a "probability distribution" is defined over the interval x in [-∞,∞], then:
∫-∞∞ f(x) dx = 1
-Suppose that a "probability distribution" is defined over the interval x in [a,d], and we wantthe probability of finding x in the interval [b,c], where a < b < c < d, then
P([b,c]) = ∫bc f(x) dx = F(c) - F(b)
Examples:
Example 1.Suppose the probability distribution is f(x)=0.2.
This is an incredably simple function (it's a constant function: y is always 0.2, for all x).
In figure 4 below, you can see the function f(x)=0.2. Since, as a probability distribution, the total area must be "1",
the function then only can be meaningful over the interval x in [0,5].
Note that the area is defined by the rectangular region bounded by f(x) and the x-axis, for x in the interval [0,5].
So, the total area is 0.2 x 5 = 1, which is exactly what we expect to find.
Now, suppose we had the probability distribution is f(x)=0.5 instead. Then the x interval neccessarily had to be [0,2],
since the total probability always have to add up to "1".
Figure 4. Simple probability distribution defined by y=0.2.
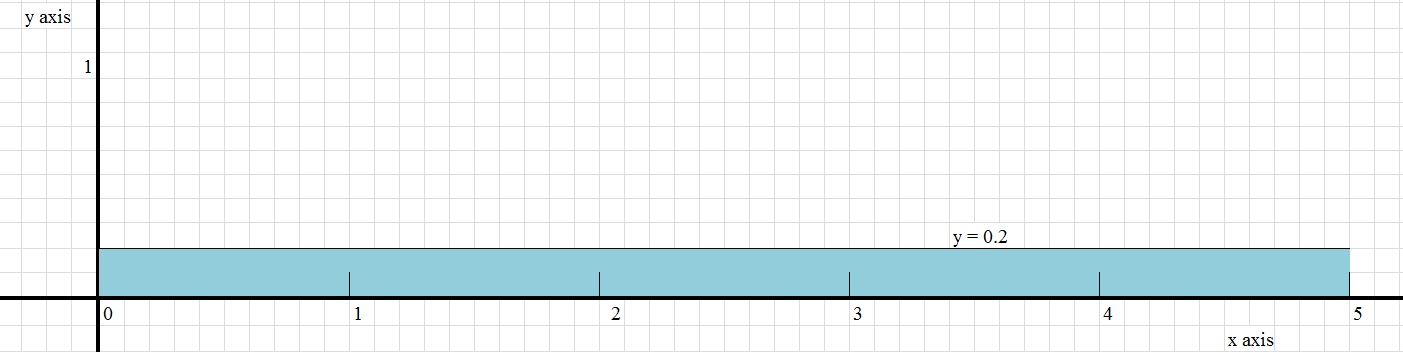
Question: what is the probability for x ≥ 4 (or 4 ≤ x ≤ 5)?
Answer:
P([4,5]) = ∫45 0.2 dx = 0.2x|45 = 0.2 * 5 - 0.2 * 4 = 0.2
Take a look also at figure 4. Note that the total area is "1". Also note that you can devidethat area in 5 parts. One such part is defined by the interval 4 ≤ x ≤ 5, so that represents
an area of 1/5=0.2.
The "trick" to find the solution is ofcourse that you knew that the primitive function of f(x)=0.2,
is F(x)=0.2x.
For more information on primitives and definite integrals: see notes 8 and 14.
True, this example used a very simply probability function. However, the principle is the same,even if it's a horrible complex function.
You can calculate probabilities, as long as you can find the primitive function.
Chapter 6. Confidence Intervals.
You may calculate a "sample mean" from a sample, but how confident are you that it representsa good measure for reality?
Indeed, you have not investigated the whole population, but you took a representative sample.
The standard deviation ofcourse, gives us a good measure for the spread of found values
with respect to the sample mean value.
Hypothetically, you could say that you are pretty confident in the keyvalues, since an interval
like [x̄ -s, x̄ +s], or even [x̄ -2s, x̄ +2s], include the far majority of observations,
and thus is a good measure for the whole Population.
But it cannot be that easy.... If you think about it, then there surely must exist requirements about the number
of observations (number of values) of your sample as well.
Things are indeed formalized into (sort of) structured protocols, in how to deal with "Confidence Intervals".
A Confidence Interval (CI) should say that we are "fairly sure', or "very sure", our true value lies in that interval.
A commonly used interval is 95%, but slightly higher CI or lower CI, might be used as well.
But, there exists at least two "forks". The two main streams are:
-We have done a traditional analysis, using a sample, which gives use a sample mean x̄ and sample standard deviation "s".
The sample mean could, for example, be a number like 12.22, or 105 etc..
This is what we have seen before, in the text above.
-An analysis using a "proportion". In this case, the sample proportion takes a value from 0 to 1, saying precisely
how many observations adhere to a certain criterium, compared to the whole sample size.
For example, you have investigated how many people in a sample, are vegetarian, which might produce a number like 0.52
if there are 52 vegetarians out of 1000 people.
Those two approaches may look similar, but all the same, still are quite different.
Here is an example, demonstrating the different approach:
-Sample mean:
Suppose your sample turns out to produce the "n" quantities (elements, values, samples):
10.2, 11.0, 9.8, 8.2, 12.3, 13.0, 12.9, 9.1, 11.3, 10.0 (the bi values)
Then the sample mean is:
| x̄ | = | 1 -- n |
Σ bi | = | 10.8 |
-Sample Proportion:
Suppose we want to know how many folks in the US are vegetarians. We ofcourse cannot interview millions of people.
Suppose we interview 1000 people. Suppose It turns out that 62 of those people are vegetarian.
Then the sample Proportion, called p̂, is defined as:
| p̂ | = | 62 -- 1000 |
= | 0.62 |
Note that the sample proportion, always is a value between 0 and 1.
Note that p̂ is a completely different entity compared to x̄.
If, for example, almost all of the interviewed people are vegetarians, then p̂ comes close to "1" (from below).
Thus, in a way, we have (at least) 2 different ways to deal with a sample from a large Population.
The following statements should actually be better formulated (more concise), however, for now, I like to say that:
-If it's pure quantitative analysis (like the lifespan of lightbulbs, weight of containers), one would probably say
that if all members are analyzed, the sample mean and sample standard deviation deliver good measures.
-If it's more like a questionaire (e.g. are you a vegetarian?), the Proportion approach delivers a good measure.
Determining the Confidence Interval of "X" %:
If you take a look again at figure 3 above, you see the graphic of the "Normal" distribution, or often also called the "Bell curve",or "Gaussian curve". However, in this case, we are dealing with a continuous stochastic variable.
It is a fact that about 68% of the measurements (or elements, values) exist in the interval [μ - σ, μ + σ].
It is also known that about 95% of the data exist in the interval [μ - 2σ, μ + 2σ].
Since the normal distribution is so common (many natural processes, events adhere to it), it is true that a CI of 95%
is commonly used too, since it nicely corresponds to [μ - 2σ, μ + 2σ].
However, with both our methods (sample mean, sample proportion), a slightly different protocol is used, but still
very similar to what we see with the common Normal distribution.
The following text describes (in a very simple way), what mathematicians see as a sort of consensus, of how
to calculate a CI with the method of sample mean, and the method of sample proportion.
⇒ CI with Sample Proportion:
Suppose you interview 500 people, on the question whether they are vegetarians.
Further suppose you found 120 people who are indeed vegetarians.
Then, in that sample, the sample proportion is:
| p̂ | = | 120 --- 500 |
= | 0.24 |
Is it possible now, to produce a statement with respect to the whole Population?
No, not with complete certainty. However, there exists a measure for a CI of 95% (and for other percentages).
To determine 95% CI, in this case, would be done like:
[p̂ - 2σ, p̂ + 2σ]
with σ defined as:
| σ | = | √ ( | p̂ (1-p̂) ------ n |
) |
It's a reasonable definition of proportion standard deviation. The number "n" is the size of the sample.
In the example above, n=500. The larger n is, the lower σ gets, and the narrower the CI interval becomes.
For our example above, we would have as σ:
| σ | = | √ ( | 0.24 (1 - 0.24;) -------------- 500 |
) | = 0.019 |
Thus, our 95% CI, is:
p̂ - 2σ = 0.24 - 2 x 0.019 = 0.20
p̂ + 2σ = 0.24 + 2 x 0.019 = 0.28
Note that p̂ must sit exactly in the middle of the interval, which is obvious since the CI
is defined to be [p̂ - 2σ, p̂ + 2σ], which in this example is [0.20 ; 0.28].
Now, the crux is this: we can say with 95% certainty that the number of vegetarions in the whole Population
is between 20% and 28%. Do not think anymore of this, that is, there is no hidden magic somewhere.
That's all there is.
Note that I "translated" the interval into percentages, which is easy to understand.
If someone demands that the CI must be (around) 99%, then an interval of [p̂ - 3σ, p̂ + 3σ]
should be calculated. Very common CI's are 95%, and in a few cases, 99%.
A rather arbitrary value like 97%, or 86%, or 92%, is hardly ever used.
Ofcourse a relation like [p̂ - N x σ, p̂ + N x σ] makes more sense, instead of some arbitrary number.
Another used %CI is 68%, which corresponds to a more narrow interval, like [p̂ - σ, p̂ + σ].
So, here we do not have a multiplier like "2" or "3", but we simply have the interval as shown above.
It can be instructive to look at figure 3 again, and watch the area below the curve change, when you make
the interval larger or smaller. For example, It should be obvious that more data is capured in [p̂ - 3σ, p̂ + 3σ] (99%),
compared to [p̂ - σ, p̂ + σ] (68%).
⇒ CI with Sample Mean:
This time, you simply calculate the "sample mean" x̄, and "sample standard deviation" S, as was shown in Chapter 2.
So, simply follow the rules of chapter 2.
The 95% CI, then can be found using:
| [ | x̄ -2 | S ---- √n |
; | x̄ +2 | S ---- √n |
] |
The calculation of the interval is pretty straightforward.
Note:
Here I use the -2 and +2 multipliers. However, in general these are approximations for a 95% CI.
In general, a factor "z" should be used, which depends on the desired CI, and the specifics
of the frequency distribution.
In this simple note, this will be ignored.