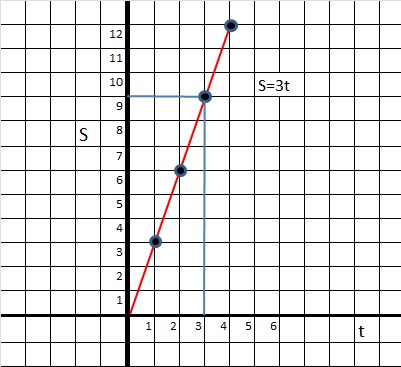
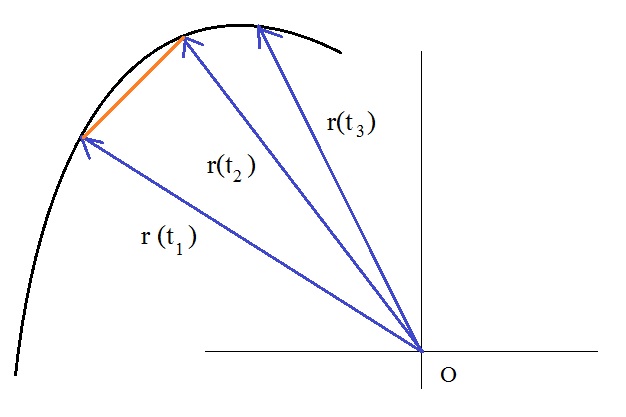
and as the second point, r(t2) at t2.
Then:
Δt = t2 - t1 (as the time interval)
and
Δr = |r(t
Then, using equation 7, filling in the numbers, would give you the average velocity.
Example 14: Calculation of the "average" velocity:
Suppose at t=0, we see a bee flying at r1=(1, -2, 6). Two seconds later, at t=2,the bee is found to be at r2=(3, -1, 4).
Question: what was it's average velocity over those 2 seconds?
We already know Δ t, which is 2 seconds.
What is Δ r? It's |r2 - r1|, or the length of the difference of those 2 vectors.
By the way, the magnitude |r2 - r1| is the same as |r1 - r2|
Thus:
Δ r = √ ( (1-1)2 + (-2 -1)2 + (6 - 4)2 ) = √ 13 = (about) 3.6
And we find as the average velocity Δ r / Δ t = 3.6 / 2 = (about) 1.8 m/s
Recap Chapter 1:
1. Theory from sections 1.1 - 1.3:
Solutions for problems, can be solved as shown in the Examples 1 to 8,using formula's as shown below.
1.1 Uniform motion (one direction), no force, constant speed (v):
v is constant.
S(t) = vt
| S'(t) | = |
d S(t) ----- dt |
= |
d (vt) ------ dt |
= | v |
1.2. Constant force, constant (uniform) acceleration (one direction):
v(t) increases with time, due to the constant acceleration.
v(t) = at
v(t) = v0 + at (if already an initial constant speed v0 was present )
S(t) = ½ at2
We also have:| S'(t) | = |
d S(t) ----- dt |
= |
d -- dt |
½ at2 | = | at | = | v |
2. Theory from sections 1.4 - 1.5 (vectorial):
Solutions for problems, can be solved as shown in the Examples 9 to 14.Velocity and acceleration must be represented by vectors if we are not working 1-dimensional.
Speed is actually the magnitude of the vector velocity.
Fundamental relations:
|
dr(t) ---- dt |
= | v(t) |
|
dv(t) ---- dt |
= |
d2r(t) ---- dt2 |
= | a(t) |
Chapter 2. Forces in Mechanics.
In physics, a number of forces are believed to be really fundamental, like the "strong (nuclear) force",the "electromagnetic force", the "weak force", and "gravity".
Classical mechanics however, is not about research, or theoretical treatment, on those fundamental forces.
It's much more involved in the actions due to forces, and thus what effects there are on macroscopic objects.
We will talk on the following subjects:
-Discussion on the unit of Force, the "Newton".
-How to get the "result" Force, if multiple forces are working on an object. This will be surprisingly easy, I am sure.
-The force of gravity on an Object on plane with a certain slope α.
-Some further Discussion on F = ma and "inertia".
2.1. The unit of Force, the "Newton" (N).
One "Newton" (N) is defined as the Force on object of 1kg, which then undergoes an acceleration of 1 m/s2.Although units are (in some way) "just" chosen, the motives for a certain choice are ofcourse "reasonable" and are based on certain
good considerations.
This is true for the Newton as well. We speak of an object of 1 kg (already an SI unit), and an acceleration
of 1 m/s2 (and the number "1" also fits nicely).
One N of force, is, on a human scale, not a gigantic force. That's why in engineering and such siences, you often
see problems formulated in such way, that people talk in numbers of "kN" (kilo Newton, or 1000 N), or for example 105 N.
-If the Force is constant, and keeps working one direction, then the formula's for a motion of a constant acceleration (section 1.3)
can be used.
-Newton's general equation "F = ma", implies that if the Force varies in time, then so does the acceleration
of the object where the force acts upon.
Note that "F = ma" is a linear equation with respect to the variables "F" and "a", if "m" is constant.
So, if we have a certain object with a certain mass, then:
If "F" increases/decreases with a factor "c", then "a" increases/decreases with the same factor "c".
"Force" is a vector, just as "velocity" and "acceleration" are.
However, if the Force works in one direction, and the motion of the object is in that direction too (say the x-axis),
then the lenght (or magnitude) of those vectors can be determined directly. We do not need to add or determine vector components etc..
The projection of those vectors on the x-axis, are directly the magnitude of the vectors themselves.
Then we can easily speak of "speed" and "force" in magnitudes (scalars) only. The "direction" is not so much important here.
Example 15:
At t=0, an object of 10kg starts to move in the +x direction, with a constant acceleration of 3 m/s2.Suppose that the force works only in the +x direction too.
Question: what is the force?
Answer:
F = ma = 10 kg * 3 m/s2 = 30 N.
Example 16:
Suppose at t=0, a force of 6N starts to act on an object of 3kg. Initially, the object was in rest.The direction of the force is exactly in line with the motion of the object.
Question:
what is the speed of the object at t=5?
Answer:
F = ma, thus a = F/m.
So, in this case, the constant acceleration is a = 6/3 =2 m/s2.
The speed after 5 seconds is v = at = 2 * 5 = 10 m/s.
Example 17:
Suppose at t=0, a force of 6N starts to act on an object of 3kg.Initially, the object had a constant speed of 6 m/s in the +x direction.
The direction of the force is exactly in line with the motion of the object.
Question:
what is the speed of the object at t=5?
Answer:
F = ma, thus a = F/m.
So, in this case, the constant acceleration is a = 6/3 =2 m/s2.
The speed after 5 seconds is v = v0 + at = 6 + 2 * 5 = 16 m/s.
Indeed, the initial speed of v0 was 6 m/s.
2.2. Forces as vectors, and determining the resultant Force.
Whichever dimension you are working in (like R2, or R3, or higher), vectors have a directionand magnitude.
If multiple forces act upon an object, simply treat them as vectors, and follow the rules for vector addition.
Simply put: using "linear algebra" works in all cases.
However, in the first subsection below, we will try "commen sense" first, and then quickly go to "linear algebra".
Note: the very basics of linear algebra, like vector addition, can be found in "math note 12".
1. The Simplest case: the vectors are all along one dimension (for example the x-axis):
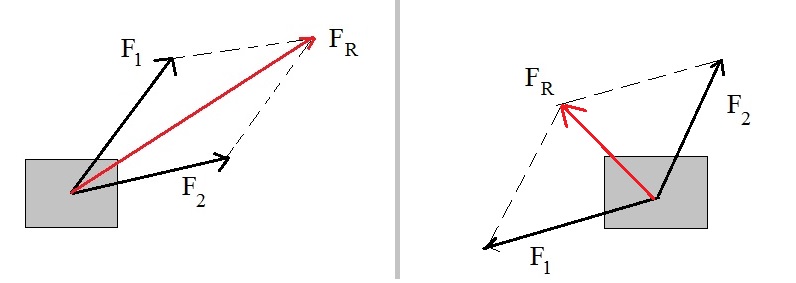
Figure 4.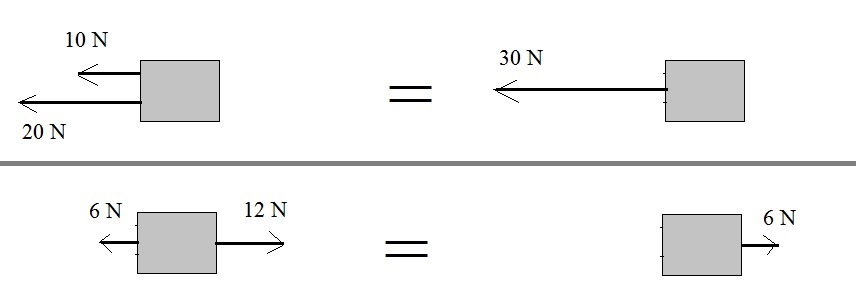
In figure 4, you see two examples of force addition, when the forces are aligned in one dimension only.
The best policy, as in any vector addition, is to determine the resultant vector.
Once having that, we can determine the length of that vector (or the magnitude of that vector).
- In the upper case in figure 4, the two forces are working in the same direction.
We can see that:
|F1| = 10N and
|F2| = 20N.
then it's obvious to see that the magnitude of the result force |FR| = 30N, since both are working
in the same directon.
- In the lower case in figure 4, the two forces are working in the opposite directions.
In this case, we cannot just add the individual magnitudes. That would result in |F1| + |F2| = 18N.
That's wrong! Magnitudes are always positive numbers. And we can clearly see that the magnitude of the resulting force just has to be 6N.
This time we really add them as vectors first:
F1 is 6N to the -x direction
F2 is 12N to the +x direction
Thus FR = 6N to the +x direction
So, thus we have |FR| = 6N
This sort of problems can be handled by "eye" and "common sense".
-However, The most consequent way to handle problems like this, is as follows:
Let's use linear algebra. The lower case shown in figure 4, suggests we have a Force in the -x direction and one in the +x direction.
It can be seen that we are working in R2.
So we can write:
| F1 = |
┌ -6 ┐ └ 0 ┘ |
| F2 = |
┌ 12 ┐ └ 0 ┘ |
Thus the resultant vector FR is:
| FR = |
┌ -6 ┐ └ 0 ┘ |
+ |
┌ 12 ┐ └ 0 ┘ |
= |
┌ -6 + 12 ┐ └ 0 + 0 ┘ |
= |
┌ 6 ┐ └ 0 ┘ |
This is correct. We have a result vector (of magnitude 6) along the +x direction.
The length or magnitude is |FR| = √ (62 + 02) = √36 = 6.
2. The General case: vectors may have any directions:
Here, you may think of any combination of vectors acting on an object, pointing in any direction.So, this could be in R2, R3, or Rn.
Figure 5 illustrates this for an R2 plane.
Figure 5.
This time, we go for using linear algebra directly. If you glance through highschool books, you may see
several other methods. However, using linear algebra is the most universal way to handle vector "stuff".
Suppose on an object we have two vectors acting on it. We want to find the resultant force and it's magnitude.
The example below is in R2. But it works the same way in R3, or Rn.
As an example, say we may represent those two vectors as:
| F1 = |
┌ -2 ┐ └ 5 ┘ |
| F2 = |
┌ 1 ┐ └ -3 ┘ |
The sum of F1 and F2 is:
| FR = |
┌ -2 ┐ └ 5 ┘ |
+ |
┌ 1 ┐ └ -3 ┘ |
= |
┌ -2 + 1 ┐ └ 5 + -3 ┘ |
= |
┌ -1 ┐ └ 2 ┘ |
So, there is our answer. We can immediately "plot" FR in R2.
However, the answer is ofcourse the resultant force in Newton, so we must find the "magnitude". If F1 and F2
were expressed in Newton units too, then |FR| is:
|FR| = √ ((-1)2 + 22) = √5.
2.3. Object on a tilted plane
This example can be found in any textbook on Mechanics.Suppose we have an object resting on a plane, while that plane is not horizontal,
but instead, has a certain angle α with the horizontal plane.
Then, what are the vector components of the Force of gravity on that object?
First of all, we know that on any object with mass "m", on Earth's surface, it is true that the force of gravity
on that object is:
Fg = mg
where "g" is the "acceleration due to gravity".So, if you climb a high tower, and you drop an object, our famous equation "F = ma" will then be "F = mg",
since the force of gravity is the only force acting on the object, with it's constant acceleration "g".
Even if an object is resting on a table, then Fg is present, although we don't observe
any acceleration. Ofcourse, the table is (usually) strong enough to resist the force, so that the object
will not simply pass through that table.
Now, the following example is actually no more than an example of the fact that a vector maybe the sum of other vectors.
Indeed, we have often seen in the mathematical notes that in many cases we can write C = A + B
where the vector C is the vectorsum of A and B.
Or, if we have some vector A in R2, which we may write as (a, b), then we can represent it as a linear combination of the
basis vectors, as A = a (1,0) + b (0,1) or, using a different notation, as A = a êx + b êy.
It actually always amounts to the "superposition" principle of vectors.
Now, take a look at figure 6.
Figure 6. Object on plane with a slope α, and the components of Fg
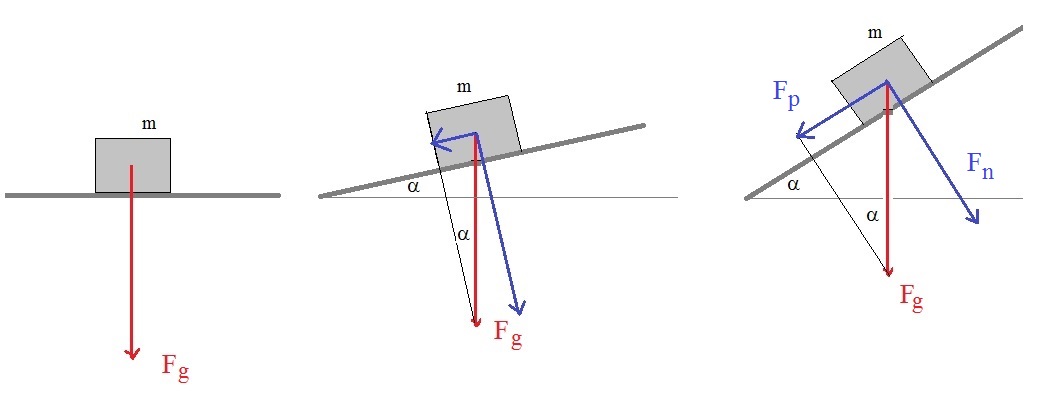
If the table is horizontal, we just have Fg = mg
If the table get's a slope α, then we may always (whatever angle α), create the vector sum:
Fg = Fp + Fn
Where Fp is the vector component parallel to the table, and Fn is
the component perpendicular to the table.
Note that if α get larger, then the Fp component increases, while Fn decreases.
Note also, that if α get's large enough, then Fp get's larger than any possible "friction"
from the table, and the object starts to move.
It's also possible, that the scenario is considered to be "friction-less", but then, in reality the object should
get into motion with any angle α.
Now, what we really are interested in, is the "length" or "magnitude" of the vector Fp,
since that component is along the only possible path where the object might start moving.
The magnitude (or length) of Fp is |Fp|.
Once we have identified a right-angled triangle defined by the segments |Fp|, |Fn|, and |Fg|,
the whole problem collapses into a simple goniometric problem.
From "math note 4" we know that:
| sin(α) = |
|Fp| ---- |Fg| |
Thus:
|Fp| = |Fg| sin(α)
|Fn| = |Fg| cos(α)
This way, it has become quite easy to calculate the magnitudes of the components, if |Fg| is known in "Newton" units.
Example 18:
Suppose we have a scenario as sketched in figure 6.
A mass "m" of 4kg rests on a tilted table, with an angle of α = 60 degrees.
Suppose further that "g" is 10 m/s2.
Question: calculate |Fp|
Answer:
|Fg| = mg = 4 * 10 = 40 Newton.
Thus:
|Fp| = 40 sin(60) = (about) 34.6 Newton.
Next, let's go to a short discussion of the equation F = ma.
2.4. Discussion of F = ma.
What exactly "mass" is, is not simple to answer.
Many philosophers and physicists broke their heads on concepts as "mass" and something called "inertia".
It's certainly not "weight". An object weights a certain amount on Earth, but it weights much less if we
would place that same object on Mars.
"Weight" is no more than a measure of how hard the local "force of gravity" is pulling on it.
So, that force of gravity, on a brick for example, is different on the Moon, if you compare it with the force of gravity
on that same brick on Earth.
Even an stronger argument: the force of gravity on Earth varies slightly with the position on Earth.
So, very small variations in weight can be observed too. However, the mass of an object is constant.
From theoretic physics, and particle physics, we know that the scalar Higgs field (which is everywhere), defines an interaction
with elementary particles, that relate "somehow" to the mass of such elementary particle.
However, such Higgs field has nothing to do with the "inertia" we see with macroscopic objects.
This concept of "inertia", is the resistance to change in momentum, that is, "it" does not want to change
it's velocity, unless a force is applied.
We know this concept very well in our macroscopic world. If you have 1kg of some stuff, you need a certain amount
of Force to set it in motion. It get's much harder to set it in motion, of you would have 10 times more of that "stuff".
In the context of classical mechanics, if we then view Newton's second law F = ma, then that "m", the mass,
must be understood as the "inerta" of that object.
So in classical mechanics, "mass" and "inertia" are likely to be the same one concept.
This is also how highschool physics books treat "mass".
On a macroscopic scale, experimentally, the equation F = ma is easy to verify, and it holds all the time.
But we have not really "explained" what is behind "inertia".
Optional reading.
If you have a certain object, then physically, a lot of it's intrinsic "energy" is due to several components,
but a large contribution is from all the "quark-gluon" soup-stuff, inside all the protons and neutrons.
This energy relates to "rest mass" according to Einstein's equation E = mc2.
Yes indeed ! Energy equals mass.
The discussion get's an additional perspective, if we consider "relativistic" machanics.
For a long time now, since Einstein's special relativity (1905), we know that the mass of an object increases
when it's velocity increases. When that velocity get's closer and closer to the speed of light, the mass get's
quickly higher and higher too..., asymptotically to infinity. Experimentally, this has been proven too in,
for example, particle physics using particle accelerators.
You see that? The energy increases, and so does it's mass. In whatever frame of reference you are, mass equals energy.
Einstein already gave you an answer as to what mass is: mass equals energy.
Before we can discuss other important concepts in classical mechanics, namely
Kinetic Energy, Potential Energy, and Work, we need to deal with the concept of "Momentum" first.
So "Momentum" is the subject of the next (relatively short) chapter.
Chapter 3. The concept of Momentum .
If you are really new to physics, then this Chapter may seem intimidating too, at first sight.
But it isn't really. Just try it.
There is a physical property of a system called "momentum", and it's absolutely indispensable for physicists.
Here is just an example: when performing "high-energy particle physics", collisions occur between elementary particles.
One main consideration when studying the results, is that physicists know that "momentum" is conserved between
the particles involved, which have always lead to insights and conclusions.
This is true for the past, the present, and undoubtly for the future too !
Momentum is not only important in Classical Mechanics. In Quantum Mechanics, Relativistic Mechanics etc..,
momentum plays an important role too.
So, what is it?
Suppose over a time interval Δt, we consider a constant force acting on an object with mass "m".
Suppose that before t BEFORE, there was no force whatsoever acting, and the constant velocity of the object was v BEFORE.
During Δt, the force acts on the object, and the object accelerates.
Suppose that after t AFTER, there is again no force whatsoever acting, and the constant velocity of the object now is v AFTER.
The timespan, over which the force acted is Δt = t AFTER - t BEFORE.
The increase in velocity, during Δt, is Δv = v AFTER - v BEFORE.
Now, the constant acceleration over Δt is:
a
=
(v AFTER - v BEFORE)
-------------
Δ t
Thus we have also:
m a
=
m
(v AFTER - v BEFORE)
-------------
Δ t
Which is the same as:
F
=
m
(v AFTER - v BEFORE)
-------------
Δ t
Which is the same as:
F Δ t
=
m (v AFTER - v BEFORE)
=
mv AFTER - mv BEFORE (equation 11)
I did not introduced any new formula here. Actually, it's only stuff we already knew before this section.
But the perspective might have changed a bit.
If we take a closer look at the "meaning" of
F Δt = mv AFTER - mv BEFORE
then we might interpret this as folows. The force F acts only for a duration of Δt,
which has as a direct consequence that the property "mv" changed by mv AFTER - mv BEFORE.
The value of "mv" can be viewed as "the quantity of motion" which an object has. You may also see it as a measure
for "mass in motion".
If a force acts upon an object, for a certain duration Δt, it's amount of motion changes by mv AFTER - mv BEFORE
The quantity "mv" is called momentum "p", so:
p = mv (equation 12)
Since "velocity" is a vector, we conclude that "momentum" is a vector too.
The magnitude of momentum is expressed in "kg m/s", due to the units in "mv".
If we have a system, of say 2 or more objects, and there is further no additional interaction (e.g. no external force),
except for those objects, then if they interact (like colliding), then total momentum is conserved.
So, in the case of 2 objects of mass "m1" and mass "m2":
p1 (before) + p2 (before) = p1 (after) + p2 (after) = Constant (equation 13)
which is the same as:
m1v1 (before) + m2 v2 (before) = m1v1 (after) + m2v2 (after) = Constant (equation 14)
Or. more generally, for "n" objects (like particles):
Σ pi = Σ mivi = constant (equation 15)
The "change" in momentum, as we can see from upper equations, is due to:
F Δt = mv AFTER - mv BEFORE = m Δ v (equation 16)
F Δt is sometimes called the "impuls" or the "action" responsible for the "change" in momentum.
Indeed:
- When a force is acting on an object, the momentum changes.
- When no force is acting on an object, the momentum does not change.
A nice illustration:
The animation below shows how the momentum (mv) from the first ball, is fully "transferred" to the last ball,
and the other way around.
Figure 7. Newton's "cradle"
(figure: from wikimedia commons).
Remember, p = mv, so p is a vector.
Since "m" is just a scalar (a number), the vectorial component "sits" in the velocity v.
In solving problems, you should always realize, that the total momentum of a system is the vector sum
of all the individual momenta of the particles, which make up the system.
Only when the particles before and after any collision, stays along 1 dimension, you can work with the magnitudes directly.
Note on "elastic" and "in-elastic" collisions:
In principle I should also explain "elastic" and "in-elastic" collisions.
Although the terms pretty much speak for themselves, there are some subtleties.
I like to wait until we have seen the concept of Kinetic Energy, which make both terms easy to explain.
Let's try some examples.
Example 19:
A ball of 10kg rolls on a frictionless table. It's velocity is 10 m/s in the +x direction.
Question: what is it's momentum?
Answer:
The magnitude of the momentum |p| = 10 kg * 10 m/s = 100 kg m/s.
The momentum as a vector is p is 100 kg m/s in the +x direction.
Or, written differently:
p = 100 ex (if ex is the unit vector along the x-axis).
The magnitude of p = |p| = 100 kg m/s.
Example 20:
This example stays in "one" dimension too.
Particle P2: is in rest on the x-axis. It's mass is 2kg.
Particle P1: moves from the left along the +x direction. Speed is 8 m/s. It's mass is 5kg.
At a certain moment, particle P1 collides against particle P2.
Directly after the collision, both are moving in the +x direction. Particle 2 now has a speed of 6 m/s.
Question: What is the speed of Particle P1?
Answer:
p1 (before) + p2 (before) = p1 (after) + p2 (after)
or:
m1v1 (before) + m2 v2 (before) = m1v1 (after) + m2v2 (after)
Thus:
8 * 5 + 0 = 5 * v1 + 2 * 6 =>
40 = 5 v1 + 12 =>
28 = 5 v1 =>
v1 = 28/5 = (about) 5.6 m/s
Example 21:
Suppose we have a collision of 2 particles.
This time we will work in multiple dimensions, so we need to take into account
that we are working with vectors.
Let's work in R2. There is no fundamental difference if you would work in R3 or Rn.
Figure 8. Adding momenta in R2
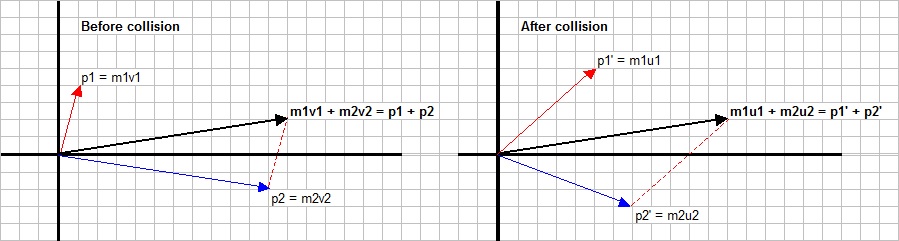
Before collision:
particle 1: mass m1, velocity v1.
particle 2: mass m2, velocity v2.
Total momentum: p1 + p2 = m1 v1 + m2 v2 = C
The "black" vector (left) in figure 8, represents the "total momentum".
After collision:
particle 1: mass m1, velocity u1.
particle 2: mass m2, velocity u2.
Total momentum: p '1 + p '2 = m1 u1 + m2 u2 = C
The "black" vector in figure 8 (right), represents the "total momentum".
Note that the "black" vector remains the same. That's conservation of momentum.
You see that? Again, linear algebra can solve a problem which at first sight looks pretty intimidating.
We know that before the collision, that the total momentum is p1 + p2.
But, after the collision, the total momentum is the same !
Thus:
m1 v1 + m2 v2 = m1 u1 + m2 u2
This is the general principle. There are several ways to find a certain unknown variable.
As we have seen before, just use vector algebra.
As an important law of physics, we have seen that the total momentum is conserved.
Chapter 4. Kinetic Energy, Potential Energy, and Work.
4.1. Short discussion on the concept of "WorK".
4.1.1 When the Force and the Displacement are "aligned" (one direction):
If a force acts on an object, and this object is in motion due to that force, then that force performs "work".
When you drag a large heavy box along some road, and you have covered 10m, you know that you have invested
quite some energy. If you cover 10m more, then the amount of invested energy has doubled.
It seems as if "Work = Force * Distance". Indeed, in it's most basic form:
W = F * s (equation 17)
Since the unit of force is the "Newton" (N), and the unit of distance is the "meter" (m), work is expressed in "Newton meter" (Nm).
As an equivalent unit, the "Joule" (J) was defined, which is the work done by a force of 1 N over a distance of 1 m.
Equation 17, must be a "scalar" variant of "something" more general, since as we know that "force" is a vector,
as well as is the position r(t) (as a vector).
However, if the force and direction are aligned along one dimension (one direction), we really can use equation 17
by simply using the "magnitudes" of the terms. So, actually we should re-write equation 17 as:
W = |F| * s (equation 17, revised)
Example 22:
Suppose a constant force of 15N acts upon an object. This force operates for some time, and in that time,
the object is displaced over 10m.
The direction of the force, and the displacement of the object, are along the x-axis.
Question: what is the work done by that force?
Answer:
Here we may apply "W=Fs", thus:
W = 15 N * 10m = 150 Nm = 150 J.
4.1.2 When there exists an angle α between the Force and Displacement:
The amount of "Work" is always a number (a scalar). In this subsection too, I will only use
the magnitude of a force vector (a scalar), and the displacement (as a scalar).
In fact, as you will see, it is sufficient to take the magnitude of the parallel vector-component of F.
How that will work out, will be shown in this subsection.
First, with any force under consideration, the only component of the Force that will do work
is the component parallel to the displacement.
For example, Consider an object in rest on a table. We know that the force of gravity is present at all times, but yet,
it does not perform work since the object stays in rest. But here, it is obvious that the force of gravity
is perpendicular to the possible path of motion of that object.
However, we can generalize that: if you have a Force pointing in any direction, then only use the component
of the force parallel to the displacement.
Here is an example:
Figure 9. Vector components of F, with a perpendicular and parallel component.
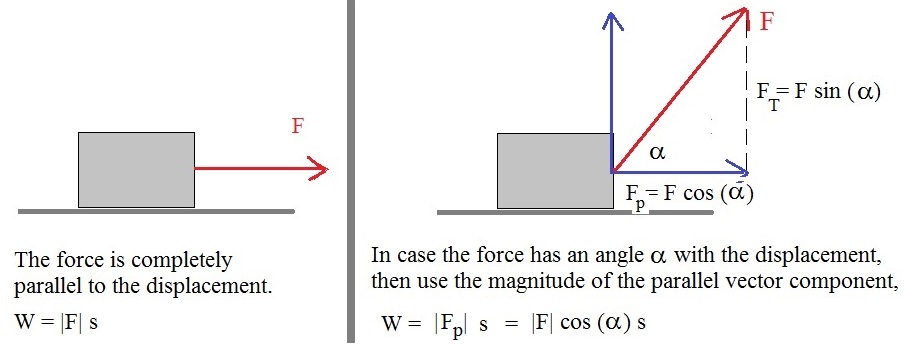
Take a look at figure 9 above. The force F is a vector, and has an angle α with x-axis.
Once we have identified a right-angled triangle defined by the lengths of |F|, |FP| and |FT|.
From "math note 4", we know that:
cos(α) =
|FP|
----
|F|
Thus:
W = |FP| s = |F| cos(α) s (equation 18)
Let's try an example:
Example 23:
Suppose a constant force F of magnitude 15N, acts upon an object. This force operates for some time, and in that time,
the object is displaced over 10m.
However, the angle between F and the x-axis is 30 degrees.
Question: what is the work done by that force?
Answer:
Only the parallel vector component of F, performs work.
We can immediately use equation 18:
W = |FP| s = |F| cos(α) s = 15N * cos(30) * 10m = 150 * cos(30) Nm = (about) 129.90 Nm = (about) 129.90 J.
4.1.3 General approach for a possible variable Force with "s", along some curved path "s":
This subsection is optional reading.
This subsection will also use the "inner product" of two vectors.
If you need to refresh your memory on the "inner product", you might want to take a look again at "Math Note 12, section 2.1".
This time, we spend a few words on the general case, of how to calculate the work a force does, over some distance "s".
However, maybe that path "s", is some "strange" curve in space, insteas of a nice straight line.
Also, the force may depend on the position in space, so it's direction and magnitude might vary per location.
Instead of some displacement "s" as a scalar (like the displacemnt along the x-axis), we should this time use
a position vector r, just like we do when we draw an arrow to some point in, for example, R3.
Note how much equation 18, already starts to looks like the inner product of F and r,
if we instead would use r instead of just "s".
In "Math Note 12, section 2.1", it was made "plausible" that if we have two vectors A and B,
then the inner product may be written as:
A · B = |A| |B| cos(α)
This scalar might be interpreted as the length of the "projection" of A on B.
This time, we have some curve defined by r, and a variable Force F(r), depending on the position r.
What we can do is to divide r into very small segments, and per segment, determine the parallel component of F(r)
at the center of that small segment. Then, determine the product of F(r) at that location and the small segment,
and then, add all products up over the trajectory where you need to calculate the "work".
This "smells" a lot like having an "Integral", if we really would make the length segments infinitesemal in size.
I'am not sure how much you are aquinted with Integrals, but usually an Integral is no more than a very large summation
of very small segments.
If the segments Δr really get's very small, then Δr will go to dr.
Figure 10. Very small segments "Δr" and the parallel component of F at Δr.
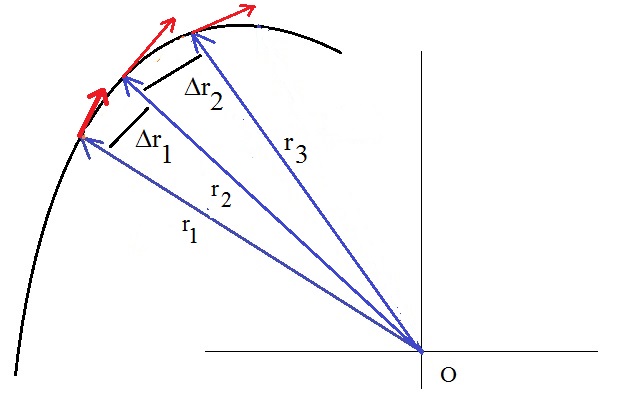
I hope you might find the following argument (reasonably) plausible.
Suppose we want an approximation of the work that a force has done, over a curved trajectory,
defined by the "starting point" P1 and "end point" P2 on that trajectory.
This trajectory will be diveded into a large number of small Δr's, so that at such Δri, the
trajectory is nearly straight. Then, at such Δri, we can calculate the product of the distance Δri,
with the magnitude of the parallel component of the force at Δri.
If you now would add up all those small products, we get:
Approximation of the Work over [P1,P2] = ∑ Fparallel, i · Δri
By letting Δri going to "dr" and thus the summation then will get infinite,
we actually get an Integral:
Work over [P1,P2] = ∫P1P2 F(r) · dr (equation 19)
Believe me: it's actually not even so hard to perform real calculations "a la" equation 19,
if we have a "reasonable" force vectorfield, and a "reasonable" trajectory.
However, this subsection was optional reading, and I like to keep this note relatively simple, and not clutter it
too much with too much detail. It's much more important that you get the general idea of the concepts discussed in this note.
4.2. Short remark on conservative force fields.
In fact, in a socalled "Conservative" force field, the work done by some force F(r) by moving an object
from point P1 to P2, is independent from the path taken.
Even if F(r) has all sorts of "angles" to the path dr, along the trajectory, we know that the contribution to the work,
is only due to the "parallel component" of F(r).
This means that the total sum of the "parallel component" times dr, will always add up to the same value.
The forces we have seen in this note, like the gravitational force on Earth, are all "Conservative".
It also implies, that if you must calculate the work done moving an object from P1 to P2, along some difficult trajectory,
and there also exists another "easier" path, you may choose that easier path in your calculation,
as long as the begin- and end points P1 and P2 are fixed.
We are not going to make "hard" calculations in this note. However, it would be great if you get the general idea
behind the concept of a conservative force field.
Figure 11. A conservative force field: the work done moving from P1 to P2, is independent of the path taken.
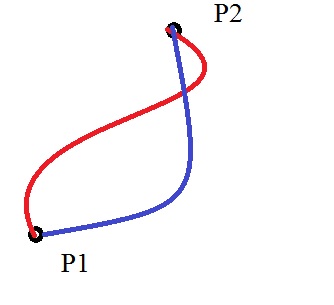
Now, let's go to a short discussion on Kinetic- and Potential Energy.
4.3. Short discussion on Kinetic- and Potential Energy.
4.3.1 What is "Potential Energy" Ep?
Please read the following two examples carefully:
Example 24: Potential Energy Ep in Earth's gravity.
Suppose you have an object of 2kg. Next, with that object, you climb a tower of a height of 30m (against gravity).
Then the work done by you is:
W = |Fg| * s = mg * h = 2*10*30 = 600 J.
In a way, "all that energy" is not "lost"!
Physicists say that the Potential Energy Ep of that object has increased by "mgh".
It's exactly the same as the work you invested by bringing it up, to a height of 30m.
If you would now drop that object, the object ofcourse falls down, with an increasing velocity
due to the constant acceleration "g".
While going down, at each point of the path, the Potential Energy drops while something called the "Kinetic Energy" grows.
This latter energy is dependent on the mass and velocity of the object.
The faster it goes, the more Kinetic Energy we can associate with that object.
In this example the "Potential Energy" Ep increased with "mgh". The rate and the amount by which the "Potential Energy" increases
is dependent on the type of force field. In this case, it's Earth's gravity, so the increase is always "mg Δh".
So, in Earth's gravity:
Ep = mg Δh
Example 25: Potential Energy of a charged particle in a static Electric Field.
This example is very similar to the case of Potential Energy due to Earth's gravity.
However, this time we take a look at an elementary particle with a positive charge "+q",
in an Electric field.
Maybe you are not so familiar with Electrostatics and charges. In short:
First of all, electric charges of the same "sign" repel each other. So, "+q1" and "+q2" repel each other.
Secondly, electric charges of opposite "sign", attract each other. So, "+q1" and "-q2" attract each other.
It's possible to have a condensator like "device", where two plates are opposite each other, and where each
plate has an opposite charge. So, say the upper is charged positively, while the lower one is negatively charged.
Then there also exists a certain voltage difference "V", between those plates.
Figure 12. Two opposite charged plates. Then there exists a "voltage difference" between those plates.
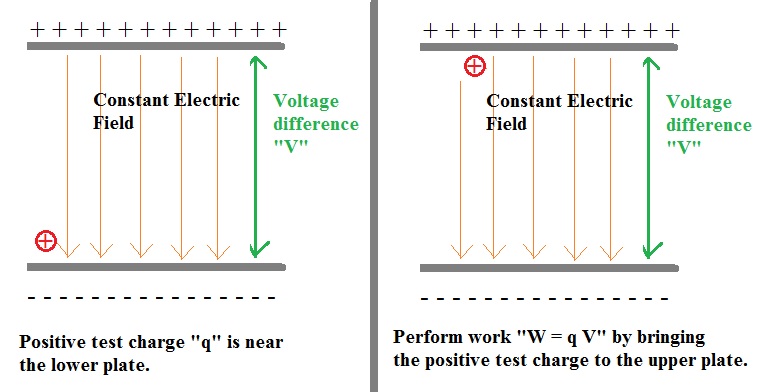
Take a look at figure 12. In the left figure, the positive test charge is near the lower plate.
This test charge, absolutely does not want to go to the upper posively charged plate.
If we move it, it will cost us energy, expressed by "work". We need to apply a force to move it
towards the posively charged plate.
It's possible that you are not familiar yet with Electrostatics, but there exists also a potential difference,
or "voltage difference" between the lower- and upperplate. Suppose that Voltage difference is "V" (or better: ΔV).
Then the work we must invest is:
W = q * V
This invested energy is not lost. The test charge aquired a Potential Energy of "qV".
Suppose we had "some way" to hold the particle near the upper plate. At the moment we let it go,
it will immediately accelerate towards the negatively charged plate.
Indeed, it is true that between the two plates a constant "Electric Force" exists, that will act
on any charged particle between the plates. In this case, when a positive test charge is involved,
the direction of the force is "downwards".
Thus, as the test charge accelerates toward the lower plate, it aquires "Kinetic Energy", while in an equal
amount the Potential Energy lowers.
Although here different physical entities and forces are involved, it is quite similar to example 24.
So, in an electrostatic field, the Potential Energy that a positive testcharge aquires (when moving to the + plate) is:
Ep = qV or, Ep = q ΔV (equation 20)
The latter expression is valid, if we would call the voltage difference between the plates "ΔV" instead of "V".
4.3.2 What is "Kinetic Energy" Ek?
Examples 24 and 25, also illustrated the concept of "Kinetic Energy" Ek.
In general, when you invest "work" to move an object or particle against a force field,
then the object or particle aquires "Potential Energy".
If you then "let it go", the object or particle immediately accelerates in opposite direction (due to the force).
When it is back at it's original position, all "Potential Energy" is converted into "Kinectic Energy".
Yes, a fundamental "law" was expressed by that latter sentence:
Conservation of Energy applied to mechanical systems using Ep and Ek:
When "work" W is invested to increase Ep, then
when the constraint is lifted, Ep is fully converted to Ek
When you decide that you have invested enough "work", then Ep=W and Ek=0
when the constraint is lifted, the object aquires an increasing Kinetic Energy Ek, up to the point
where Ep=0 and Ek=W
At any point "in between" (for example during the fall of an object), Ek and Ep are "balanced",
meaning "Ek + Ep = W".
Although the amount of the Potential Energy depends on the type of Physical system (e.g like Earth's gravity, where Ep = mgh),
there indeed exists a uniform equation for the "Kinetic Energy" Ek.
Using "plain logic" dictates that Ek must depend on the mass "m". The higher the mass is, the more "Kinetic Energy" is involved.
Secondly, Ek must also depend on the speed "|v|", since the higher the speed is, again the more "Kinetic Energy" is involved.
There exists a simple derivation to find the formula of Ek. In principle, for the general case, I should use an "integral" again.
However, if we take example 24 is an "archetype", then we may say:
Total Work done = W = F * s (where s is for example the height).
Then we let the object go, and it accelerates downwards.
Then:
W = Fs = ma * s = ma * ½ at2.
At any moment during the fall, "v=at", so a=v/t. Substituting that into the equation above, gives us:
W = F * s = mas = ma * ½ a t2 = ½ m a2 t2 = ½ m (v2 / t2) t2 = ½ m v2
Although not "nicely" derived for the general case, I think that it is made plausible that in mechanical systems, it holds that:
Ek = ½ m v2 (equation 21)
Example 26:
Suppose an object of 2kg, is lifted to a height of 30m.
Then, we drop the object.
Question: what is the speed of the object when the Potential Energy has dropped to half of it's max value?
Answer:
When at height of 30m, then:
Ep = mgh = 2 * 10 * 30 = 600 J.
When Ep is lowered to 300 J, then Ek has increased to 300 J.
Thus, according to Ek = ½ m v2
300 = ½ m v2 =>
300 = ½ 2 v2 =>
300 = v2 =>
v = √ 300 = (about) 17.3 m/s
Another Question: what is Ek when the object hits the floor?
Since the object aquired an Ep of 600 J at 30m, this then will be the
Kinetic Energy when the object hits the floor again.
Best practice:
It's probably best if you deal with this sort of problems in the following way.
The total energy is constant, so we may write an energy "balance":
Ebegin = Eend
So, in the example where a mass is at the top of a tower, and we push it over the edge,
we can write an energy "balance". Suppose the mass is 0.5 kg and the height of the tower is 30 m.
Ebegin = Epot + Ekin = mgh + 0 = 0.5 * 9.81 * 30 = 147.15 Joule.
Eend = Epot + Ekin = 0 + ½mv2= 147.15 Joule.
From this, you can easily calculate the endspeed when the object hits the ground.
Now, suppose we may not neglect the friction with the air, when the object is falling down.
In that case, the energy equation will be:
Ebegin = Epot + Ekin = mgh + 0.
Eend = Epot + Ekin + Q = 0 + ½mv2 + Q.
Here, "Q" is the heat which arose due to the friction, and ofcourse this time the endspeed
will be somewhat lower compared to the example before.
Sometimes, in some problem (say an exam question), the force of friction is known, and you may
further assume that it is constant during the fall of the object.
It may help you to calculate "Q", using W = Ffric * s.
Often such exam questions provide some extra details by which you are able to calculate the endspeed
of the object in such situations.
Anyway, my main objective here was to make you aware of the "energy balance".
Chapter 5. Harmonic oscillators in classical Mechanics.
In "math note 10", I tried to discuss several harmonic oscillators, from the perspective of "differential equations".
This time, I like to use a typical Highschool approach. This mainly means that the material below, often treat
many physical quantities as scalars. However, this approach works, and allows you to solve all sorts of problems.
There are countless examples of harmonic ocillators, like the "pendulum", "particle in a box", etc...
However, the "uniform circular motion" is (sort of ) the standard example. Let's discuss that one.
In this case, an object (or particle), performs a circular motion (with radius "R") around an origin,
with a constand orbital speed "vT".
Using the subscript "T", I like to make clear that this "vT", is always "tangent" to the path of motion.
Figure 13. Uniform circular motion. Note also the projections on the x- and y-axes.
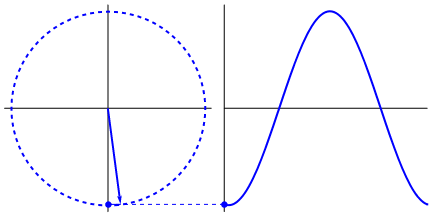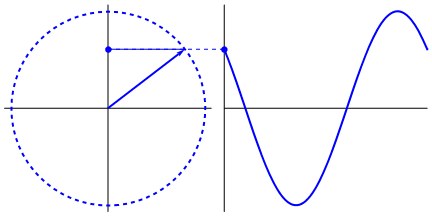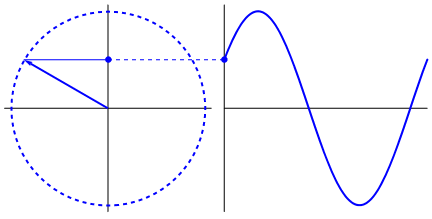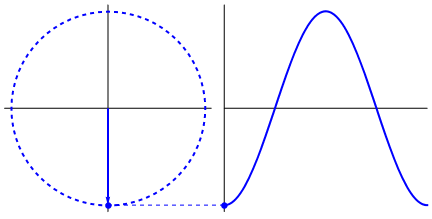
About the figure: from "wikimedia commons" (public domain).
Orbital speed vT:
Suppose the radius of the circle is "R". Then the circumference of the circle is 2πR.
Also, suppose that the time to complete one full circle is T seconds.
Then, since vT is constant, and based on equation 1, we find:
vT
=
S
--
t
=
2πR
--
T
(equation 22)
Angular speed ω:
In T seconds (also called "the Period"), our particle completes a full circle of 2π (rad).
So, it is possible to define an "angular speed", meaning "how much" angle has the radius R completed in time "t"?
This angle then, is the angle between R and the x-axis.
One thing is for sure: in T it does 2π (rad).
Different cicular motions, will have a different T and a different vT ofcourse.
So, T indeed characterizes the "angular speed" (ω) of a certain circular motion.
Since ω also is the answer to the question "how much angle has the radius R completed in time t"?
we may define the following equation for ω:
ω
=
2π
--
T
=
Δ θ
--
Δ t
(equation 23)
Ofcourse, in the case of a uniform circular motion, ω is constant, as can be seen from equation 23.
If T (the constant Period) is known, then ω is known too, by using equation 23.
However, θ changes by time. If we know the constant ω, then in a certain timeslot "t", θ has increased by "ω t".
Thus we also have:
θ = ω t (equation 23' - note the accent in 23')
Often in figures like figure 14, the angle between R and the x-axis is denoted by α. However, in most textbooks
and articles about harmonic oscillators, that same angle is often called θ, and I think I better to conform to conventions.
(Ofcourse, it does not matter at all which letter one uses for denoting an angle).
Relation of vT and ω:
We can also express vT in terms of ω and R. Simply take a look again at equations 22 and 23.
It then immediately follows that
vT
=
2πR
--
T
=
ωR
(equation 24)
Projections of R on the x-axis and y-axis:
Actually, this was all already in "math note 4". If your memory on sin() and cos() are a bit hazy,
then please consult "math note 4" again.
Figure 14. The projections on the x- and y-axes expressed in sin(θ) and cos(θ).
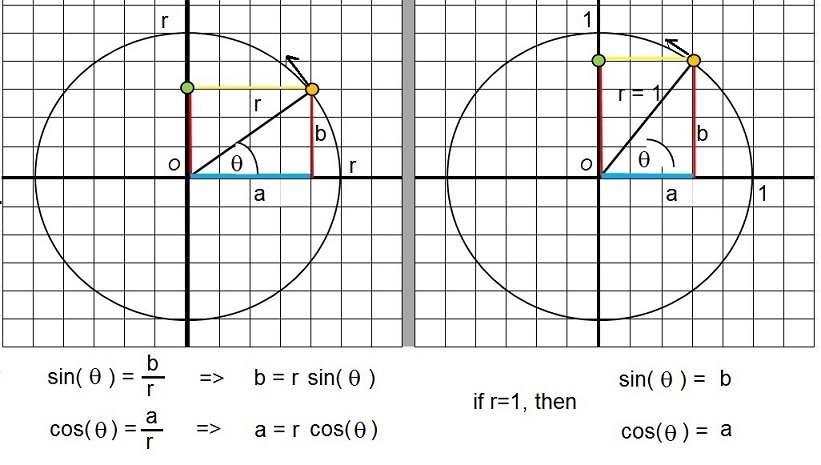
In fact, by looking at figure 14, and memorizing the pure definitions of sin() and cos(), we know that at any specific time "t":
projection of R on the x-axis: a = R cos(θ)
projection of R on the y-axis: b = R sin(θ) (equations 25)
But the object is moving in a circular motion. So, θ changes all the time, or more exactly, by time,
at the constant rate of ω
This means that the "time-dependent" equations for the projections on the x- and y- axes, are:
time dependent projection of R on the x-axis: x(t): x(t) = R cos(ωt)
time dependent projection of R on the y-axis: y(t): y(t) = R sin(ωt) (equations 26)
This also means that we can easily find the vx and vx components of the
speed vT (or |vT|), at any time "t". We simply differentiate x(t) and y(t) with respect to t.
vx(t) = d/dt R cos(ωt) = -ωR sin(ωt)
vy(t) = d/dt R sin(ωt) = ωR cos(ωt) (equations 27)
Movement of the dot on the y-axis:
Figure 13 is quite nice indeed. But also note the "dot" moving up and down on the y-axis.
Actually that dot (and the dot on the x-axis, which is not visible), performs a harmonic oscillation.
It's displacement is characterized by a "sin(t)" or "cos(t)" like function.
If you would attach a small pen on such dot, and roll a piece of paper with a constant speed under that pen,
you really would get a "sin(t)" or "cos(t)" function on paper.
Note that throughout section 5.1, all equations are in scalar form. It can all also be done using a vectorial approach.
However, the theory sofar holds ok.
For example, if you know T and R, it's easy to calculate ω or vT as scalars,
but that is really good enough.
Where is the Force ?:
Something is still missing. Yes, there has to be a "centripetal force", that is always perpendicular to vT,
and pointed towards the Origin at all times.
Only then, it is possible that an object turns around an origin in a circular fashion, with a constant speed vT.
You probably have experimented with such scenario (as a kid?), with a mass on a rope, and turn it around and around,
and you yourself in fact created (or excerted) that force (through the tension of the rope).
A "strange" thing might be, that the work done by the force is "0".
As we have seen in chapter 4, in the end, only the parallel component contributes to work, and in this case,
the force is always perpendicular.
Also, since vT stays constant, that may help to convince you too, that no work is done.
Note: the term "centripetal force" is questioned by some folks, and they rather only like to speak of "centripetal acceleration" as a better term.
So, what are the expressions for the "centripetal force" Fc and "centripetal acceleration" ac?
By the way, the tangent components are absent. The speed remains constant, thus there is no "tangent acceleration" aT.
Likewise, there is not tangent (or parallel) component of the Force present: The force is always perpendicular to vT.
Here I will only list the magnitudes of the "centripetal force" and "centripetal acceleration":
aT
=
vT2
--
R
(equation 28)
FT
=
mvT2
--
R
(equation 29)
Note that the equations 26 and 27, really describes the motions of the "dots" on the x-axis and y-axis,
and form the "heart" of the harmonic motion example of this section.
5.2 Other harmonic oscillators.
The "Pendulum":
Since the Pendulum is also a subject of "math note 10: differential equations Part 1, section 2.3".
I may say that you check that section in "math note 10".
However, it is based on deriving the "differential equation" first, and next find the solutions to that equation.
Mass (damped or undamped) on a spring:
This too is also a subject of "math note 10: differential equations Part 1, section 2.2".
But again, here too I first try to find the "differential equations" and next I try to find solutions.
Many other examples are available.
My text in "math note 10", using differential equations, might be percieved as pretty difficult....
However...:
Maybe it's a nice task to "Google" on keywords as the "Pendulum" or "equations of the Pendulum",
and try to find a nice easy article on the motion of the Pendulum.
It's never a bad idea to see some other perspectives too.
Or, you can also rightfully say, that you first want to see some completely other subjects of Classical Physics.
Indeed, lots of stuff is not in this note, like "angular momentum", "classical waves" etc.. etc..
There is a lot more you can study, which is a great thing.
Chapter 6. Gravitation and potential Energy.
This chapter is very limited. For example, it does not cover orbital mechanics, and other
matters important for satellite orbits, planets, trajectories etc..
6.1. Newton's Law of Gravity.
According to Newton, any two masses M1 and M2, exert an attractive gravitational force between them.
However, in the microscopic realm (atoms, elementary particles), the force is so increadably weak, that it is unmeasurable
for any practical purposes. Mind you: here we discuss the "classical" view on Gravitation.
But on a macroscopic scale, say in effect in the Solar system (Planets, Sun, comets etc..), Newton's law
works amazingly well. Newton's law of gravitation is:
F =
G
M1 * M2
--------
r2
Here, M1 and M2 are the masses of the two objects (in kg), "r" is the distance between them (in m),
F is the force (in N), and G is the socalled "gravitational constant".
G has been determined to be 6.673 * 10-11 N m2/kg2.
Newton arrived to this equation, by deduction, and interpreting observations. But the equation sounds absolutely logical.
We may indeed assume, that the higher M1 and/or M2 are, the larger the Force will be.
Also, if the distance increases, we may expect that the Force will decrease, which is accounted for by "r
"
in the denominator of the equation. So, the equation "looks" sound enough.
In Newton's framework, it is indeed so that the Force that M1 exerts on M2, is exactly the same
as M2 exerts on M1.
If you look at the Solar system, the mass of the Sun is so large, that the Planets orbit the Sun.
You can use Newton's equation for calculations involving the Sun and Planets, or sattelites orbiting Earth etc..
Example:
Here is an example. Suppose a Person of 70kg is at the surface of Earth. What is the force that the Earth excerts on this person
(and ofcourse the other way around)?
If we take:
G = 6.673 * 10-11 N m2/kg2, r=6.38 x 106 m (radius Earth), M1 =70kg, M2=6*1024 kg (mass Earth),
Then we have:
F =
6.673 * 10-11
70 * 6*1024
--------------
(6.38 x 106)2
which is about 688 N.
6.2. Gravitational potential energy.
If two masses are (relatively) close, one can address the Gravitational potential energy of one system
in the gravitational field of the other system.
Usually, one system (M1) is substantially smaller than the other (M2), like a Planet in the field of a Star, or
a sattelite in the gravitational field of Earth etc..
Suppose, the distance between the objects is "r". Then the potential Energy of M1 is:
Epot, M1 =
- G
M1 * M2
--------
r
You may have two questions. Why the "-" sign, and what happened to the quadratic power of "r"?
To start with the latter: You know that W = F * s. So, Energy is equal to Force x Distance.
The Force has a quadratic term in the denominator, and we have a multiplication with "distance" (r),
which leads to the equation shown above.
I immediately admit that this is a bit of a "Jip and Janneke" explanation.
Better is, to review the amount of work needed, to bring an object of mass M1, located at infinity,
thus where it's potential Energy with respect to M2 must be "0", and then move it nearer and nearer,
all the way up to distance "r" from Mq2. This is an integral, and it looks a bit like:
Work of F from infinity to r =
∫infr G
M1 * M2
--------
r2
dr
If you know math, then you might know that the primitive of r-2, is -r-1,
which then explains the formula of the gravitational potential, and the negative sign.
However, if you are like me, the negative sign is not explained adequately enough.
Ok...
If I would say that only relative values matter, you might start laughing, although it's really so.
I mean, the temp difference between 1000K and 1100K, is not different as in 10000K and 10100K.
But as you carry a brik upwards a tower, it's potential energy might increase from 0 to e.g. 100 J.
Indeed, the higher the altitude, the more positive the potential energy becomes. Yes? Yes.
But that's the same as if it would increase from -300 J to -200 J, which is a positive increment of +100 J.
But in Highshool questions/tasks, it is often presented as being absolute values. Ofcourse, if we take
a brick upwards a tower, it's potential energy goes up with 100 J.
If we then let it fall, Ekin will go up and Epot will go down.
Falling at the ground, Epot is zero, and Ekin reached it's maximum (Ekin in value, was just what Epot was at the top).
Now, suppose, you discover a hole in the ground. It's 100m deep. It seems that the ground the brick is on,
is not Epot=0, since you can drop the brick into the hole.
So, it's a bit arbitrary, in the sense that absolute values are often meaningless, but differences
(in height, and thus in Epot), do matter.
For about the gravitational potential, for which we can see the formula above:
- As r increases, so does Epot, although it gets less negative. It seems correct.
- As r is very, very large, two masses M1 and M2 are disconected in any way,
so it makes sense that Epot nears zero.
- Mathematically, we simply arrive at the formula about, which describes the behaviour of Epot.
Since Epot, M1 resembles a y= - 1/x function (since r is in the denominator), a rough
graph of Epot, M1 is shown below.
At a larger distances, Epot, M1 is getting nearer and nearer to "0".
Figure 15.
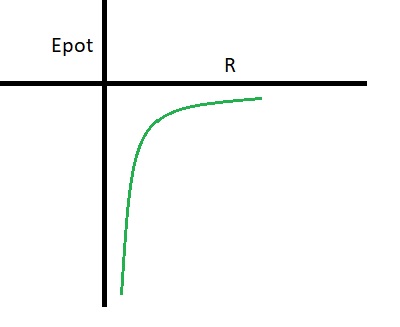
Keep in mind that the sketch above, is no more than a graphical represention of the formula
for Epot, as derived above.
For n illustrative example, see exercise 5 below.
6.3. The escape velocity.
What velocity do you need, to "just" escape the gravity of a larger mass? In such cases, we assume that the
object that needs to escape (like a rocket), must have a minimal energy, or a minimal speed,
to "just" get out of the attractive gravitational field (the force) of a large mass (like a planet as
Jupiter, Mars, Earth, or any other larger mass).
It's the "minimum" speed, so, at a large enough distance, the speed may even go to "near 0".
And Ekin is going to 0 as well. So, we are looking for that minimum amount of speed (or energy).
Usually, one calculates that, when the smaller object (the rocket) is on the surface of the larger mass,
but it may also already be in orbit (although then obviously the numbers will be different).
There are several approaches to find the escape velocity. We know the expression for the "centripal Force",
as was shown in equation 29. You can equal that to the gravitational force, as shown above.
With a bit of rearrangements, you can find the formula.
It's even easier to use an energy balance. We can write down the general equation for the initial kinetic energy
required, and equal that to the potential energy. The total energy at the start (on the surface) is 0,
that is, Ekin + Epot = 0. So:
½ m * vesc2
+
- G
m * M
-----
r
= 0
So:
½ m * vesc2
=
G
m * M
-----
r
On both sides of the equation, we have "m", so we can eliminate that. It's amazing that we can do that,
because then it turns out that vesc is independant of "m". That's amazing. Did you expect that?
½ vesc2
=
G
M
--
r
From here, it is quite easy to find that:
vesc
=
√ (
2GM
----
r
)
Additional exercises:
Exercise 1:
Suppose we have a track in the form of a circle. A small ball of 31 gram
is mounted at the top. The radius of the track is 42 cm.
The angle α is 50 degrees.
At t=0, we release the ball, and the ball leaves the track at point C.
You may neglect any form of friction.
See the figure below.
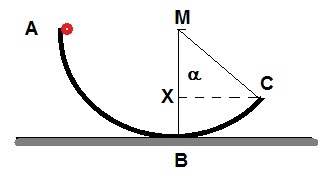
1. What is the amount of work which gravity performed up to point C ?
2. Suppose the track delivers 2.5 N of force Fw due to friction.
Which total amount of work is performed by Fw?
3. What is the velocity of the ball at point C (no friction) ?
Part 1.
At the top, Ep + Ek = mgh + 0 = 0.031*0.42*9.81 = 0.128 J
At the bottom Ep + Ek = 0 + ½mv2 = 0.128 J
The above facts are nice to know, but we can do the calculation as follows:
We only need the height difference between A and C. This way, we can find Ep,
which will is exactly the positive amount of work performed by gravity.
cos(α) = MX/MC.
cos(50) = MX/MC
0.643 = MX /0.42 => MX= 0.643 * 0.42 = 0.27 m.
=> XB = 0.42-0.27= 0.15.
Ep at height X = 0.15 * 0.031 * 9.81 = 0.045 J. This amount is "negative".
Ep difference point A to X = 0.128 - 0.045 = 0.083 J = 8.3 * 10-2
The work done by gravity at point C is netto 8.3 * 10-2 J.
Can it be analyzed in a much simpler fashion?
You only need to know the height difference between A and C.
Ep=W=mgh=m * g * r*sin(90-40) = 0.031 * 9.81 * (0.42 * sin(90-40)) = 8.3 * 10-2 J.
Part 2.
We need to know the length of the arc ABC. Call this length "S".
Then we can apply W = F * S.
Circumference circle = 2 * π * r = 2 * π * 0.42.
The arc ABC is the part (90+50) degrees / 360 degrees of the total Circumference circle.
S = 2 * π * 0.42 * (140/360) = 1.02m.
W = 2.5 * 1.02 = 2.55 J.
Part 3.
Try this yourself.
Exercise 2:
Suppose a Person of 70kg is at the surface of Earth. What is the force that the Earth excerts on this person
(and ofcourse the other way around)?
We must use:
F =
G
M1 * M2
--------
r2
If we take:
G = 6.673 * 10-11 N m2/kg2,
r=6.38 x 106 m (radius Earth),
M1 =70kg,
M2=6*1024 kg (mass Earth),
Then we have:
F =
6.673 * 10-11
70 * 6*1024
--------------
(6.38 x 106)2
which is about 688 N.
Exercise 3:
A steel bal rests on the floor. Someone, with hammer, hits the bal, and this ball
rolls along a road, untill it slowly stops due to friction.
- The ball is 1.5kg.
- The distance "d" covered is 25m, before it comes to rest.
- The force of Friction Fw is 15 N.
What was the initial velocity, immediately after the hammer hits this ball?
½ m v2 = Fw * d
½ 1.5 v2 = 15 * 25
v2 = (15 * 25) * 2 / 1.5 = 500 => v= √500 m/s (is about 22.4 m/s)
Exercise 4:
At t=0, an object is traveling with a constnt speed of 10 m/s.
At the same time, an unknown but constant friction sets in, and after 10 seconds,
the object comes to a halt.
See the figure below.
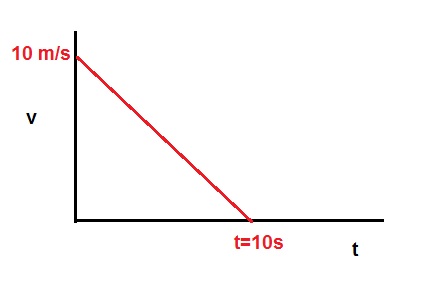
What is the distance S covered by the object?
There are multiple ways to calculate this:
Method 1.
The initial speed = 10 m/s. The end speed is 0 m/s.
So, the average speed is 5 m/s.
S = vaverage * t = 5 * 10 = 50m.
Method 2.
S = v * t.
Just like with a rectangular, the Surface is length * height. This principle works here too.
So, calculate the Surface of the triangle:
S = ½ * v * t = ½ * 10 * 10 = 50.
Question: Are you happy with the shape of the function, which is a line?
Yes. It's a constant accelertion or decelleration, so v=at is a linear function of "t", and a is constant.
Here we would have:
v(t) = v0 + at
v(t) = 10 + at (in this case, a is negative).
Would you be able to calculate the decelleration?
0 = 10 + a * 10 => a * 10 = -10 => a = -1 m/s2.
Exercise 5: Gravitational potential energy.
Suppose, on the surface of Earth, we have a payload of 400kg, which we must lift
to the International Space Station ISS.
This example, does not illustrate a rocket launch, because a rocket must develop a high
kinetic energy, or speed, to be able to stay in orbit around the Earth.
So, this example deals with gravitational energy only.
The ISS is about 450km above Earth. The Earth has a certain radius, and the ISS has a radius
of it's orbit which is 450 km larger.
G = 6.673 * 10-11 N m2/kg2
m: Mass payload: 400kg
ME: Mass Earth: 5.96 * 1024kg
rEarth=6.37*106m = 6370000m
rorbit = rEarth + 450000m=6370000m + 450000m = 6820000m
Δ Epot
=
Epot, orbit - Epot, Earth
=
-G*ME*m
--------------
rorbit
-
-G*ME*m
--------------
rEarth
It's quite a calculation, and I leave it up to you.
But you should arrive at a positive number.
That's it. Hope you liked it.
-------------
Δ t
-------------
Δ t
-------------
Δ t
----
|F|
This time, we have some curve defined by r, and a variable Force F(r), depending on the position r.
What we can do is to divide r into very small segments, and per segment, determine the parallel component of F(r)
at the center of that small segment. Then, determine the product of F(r) at that location and the small segment,
and then, add all products up over the trajectory where you need to calculate the "work".
This "smells" a lot like having an "Integral", if we really would make the length segments infinitesemal in size.
I'am not sure how much you are aquinted with Integrals, but usually an Integral is no more than a very large summation
of very small segments.
If the segments Δr really get's very small, then Δr will go to dr.
Figure 10. Very small segments "Δr" and the parallel component of F at Δr.

I hope you might find the following argument (reasonably) plausible.
Suppose we want an approximation of the work that a force has done, over a curved trajectory,
defined by the "starting point" P1 and "end point" P2 on that trajectory.
This trajectory will be diveded into a large number of small Δr's, so that at such Δri, the
trajectory is nearly straight. Then, at such Δri, we can calculate the product of the distance Δri,
with the magnitude of the parallel component of the force at Δri.
If you now would add up all those small products, we get:
Approximation of the Work over [P1,P2] = ∑ Fparallel, i · Δri
By letting Δri going to "dr" and thus the summation then will get infinite,we actually get an Integral:
Work over [P1,P2] = ∫P1P2 F(r) · dr (equation 19)
When "work" W is invested to increase Ep, then
when the constraint is lifted, Ep is fully converted to Ek
When you decide that you have invested enough "work", then Ep=W and Ek=0
when the constraint is lifted, the object aquires an increasing Kinetic Energy Ek, up to the point
where Ep=0 and Ek=W
At any point "in between" (for example during the fall of an object), Ek and Ep are "balanced",
meaning "Ek + Ep = W".
with a constand orbital speed "vT".
Using the subscript "T", I like to make clear that this "vT", is always "tangent" to the path of motion.
Figure 13. Uniform circular motion. Note also the projections on the x- and y-axes.

About the figure: from "wikimedia commons" (public domain).
Orbital speed vT:
Suppose the radius of the circle is "R". Then the circumference of the circle is 2πR.Also, suppose that the time to complete one full circle is T seconds.
Then, since vT is constant, and based on equation 1, we find:
| vT | = |
S -- t |
= |
2πR -- T |
(equation 22) |
Angular speed ω:
In T seconds (also called "the Period"), our particle completes a full circle of 2π (rad).So, it is possible to define an "angular speed", meaning "how much" angle has the radius R completed in time "t"?
This angle then, is the angle between R and the x-axis.
One thing is for sure: in T it does 2π (rad).
Different cicular motions, will have a different T and a different vT ofcourse.
So, T indeed characterizes the "angular speed" (ω) of a certain circular motion.
Since ω also is the answer to the question "how much angle has the radius R completed in time t"?
we may define the following equation for ω:
| ω | = |
2π -- T |
= |
Δ θ -- Δ t |
(equation 23) |
Ofcourse, in the case of a uniform circular motion, ω is constant, as can be seen from equation 23.
If T (the constant Period) is known, then ω is known too, by using equation 23.
However, θ changes by time. If we know the constant ω, then in a certain timeslot "t", θ has increased by "ω t".
Thus we also have:
θ = ω t (equation 23' - note the accent in 23')
Often in figures like figure 14, the angle between R and the x-axis is denoted by α. However, in most textbooksand articles about harmonic oscillators, that same angle is often called θ, and I think I better to conform to conventions.
(Ofcourse, it does not matter at all which letter one uses for denoting an angle).
Relation of vT and ω:
We can also express vT in terms of ω and R. Simply take a look again at equations 22 and 23.It then immediately follows that
| vT | = |
2πR -- T |
= | ωR | (equation 24) |
Projections of R on the x-axis and y-axis:
Actually, this was all already in "math note 4". If your memory on sin() and cos() are a bit hazy,then please consult "math note 4" again.
Figure 14. The projections on the x- and y-axes expressed in sin(θ) and cos(θ).

In fact, by looking at figure 14, and memorizing the pure definitions of sin() and cos(), we know that at any specific time "t":
projection of R on the x-axis: a = R cos(θ)
projection of R on the y-axis: b = R sin(θ) (equations 25)
But the object is moving in a circular motion. So, θ changes all the time, or more exactly, by time,at the constant rate of ω
This means that the "time-dependent" equations for the projections on the x- and y- axes, are:
time dependent projection of R on the x-axis: x(t): x(t) = R cos(ωt)
time dependent projection of R on the y-axis: y(t): y(t) = R sin(ωt) (equations 26)
This also means that we can easily find the vx and vx components of thespeed vT (or |vT|), at any time "t". We simply differentiate x(t) and y(t) with respect to t.
vx(t) = d/dt R cos(ωt) = -ωR sin(ωt)
vy(t) = d/dt R sin(ωt) = ωR cos(ωt) (equations 27)
Movement of the dot on the y-axis:
Figure 13 is quite nice indeed. But also note the "dot" moving up and down on the y-axis.Actually that dot (and the dot on the x-axis, which is not visible), performs a harmonic oscillation.
It's displacement is characterized by a "sin(t)" or "cos(t)" like function.
If you would attach a small pen on such dot, and roll a piece of paper with a constant speed under that pen,
you really would get a "sin(t)" or "cos(t)" function on paper.
Note that throughout section 5.1, all equations are in scalar form. It can all also be done using a vectorial approach.
However, the theory sofar holds ok.
For example, if you know T and R, it's easy to calculate ω or vT as scalars,
but that is really good enough.
Where is the Force ?:
Something is still missing. Yes, there has to be a "centripetal force", that is always perpendicular to vT,and pointed towards the Origin at all times.
Only then, it is possible that an object turns around an origin in a circular fashion, with a constant speed vT.
You probably have experimented with such scenario (as a kid?), with a mass on a rope, and turn it around and around,
and you yourself in fact created (or excerted) that force (through the tension of the rope).
A "strange" thing might be, that the work done by the force is "0".
As we have seen in chapter 4, in the end, only the parallel component contributes to work, and in this case,
the force is always perpendicular.
Also, since vT stays constant, that may help to convince you too, that no work is done.
Note: the term "centripetal force" is questioned by some folks, and they rather only like to speak of "centripetal acceleration" as a better term.
So, what are the expressions for the "centripetal force" Fc and "centripetal acceleration" ac?
By the way, the tangent components are absent. The speed remains constant, thus there is no "tangent acceleration" aT.
Likewise, there is not tangent (or parallel) component of the Force present: The force is always perpendicular to vT.
Here I will only list the magnitudes of the "centripetal force" and "centripetal acceleration":
| aT | = |
vT2 -- R |
(equation 28) |
| FT | = |
mvT2 -- R |
(equation 29) |
Note that the equations 26 and 27, really describes the motions of the "dots" on the x-axis and y-axis,
and form the "heart" of the harmonic motion example of this section.
5.2 Other harmonic oscillators.
The "Pendulum":Since the Pendulum is also a subject of "math note 10: differential equations Part 1, section 2.3".
I may say that you check that section in "math note 10".
However, it is based on deriving the "differential equation" first, and next find the solutions to that equation.
Mass (damped or undamped) on a spring:
This too is also a subject of "math note 10: differential equations Part 1, section 2.2".
But again, here too I first try to find the "differential equations" and next I try to find solutions.
Many other examples are available.
My text in "math note 10", using differential equations, might be percieved as pretty difficult....
However...:
Maybe it's a nice task to "Google" on keywords as the "Pendulum" or "equations of the Pendulum",
and try to find a nice easy article on the motion of the Pendulum.
It's never a bad idea to see some other perspectives too.
Or, you can also rightfully say, that you first want to see some completely other subjects of Classical Physics.
Indeed, lots of stuff is not in this note, like "angular momentum", "classical waves" etc.. etc..
There is a lot more you can study, which is a great thing.
Chapter 6. Gravitation and potential Energy.
This chapter is very limited. For example, it does not cover orbital mechanics, and othermatters important for satellite orbits, planets, trajectories etc..
6.1. Newton's Law of Gravity.
According to Newton, any two masses M1 and M2, exert an attractive gravitational force between them.However, in the microscopic realm (atoms, elementary particles), the force is so increadably weak, that it is unmeasurable
for any practical purposes. Mind you: here we discuss the "classical" view on Gravitation.
But on a macroscopic scale, say in effect in the Solar system (Planets, Sun, comets etc..), Newton's law
works amazingly well. Newton's law of gravitation is:
| F = | G |
M1 * M2 -------- r2 |
Here, M1 and M2 are the masses of the two objects (in kg), "r" is the distance between them (in m),
F is the force (in N), and G is the socalled "gravitational constant".
G has been determined to be 6.673 * 10-11 N m2/kg2.
Newton arrived to this equation, by deduction, and interpreting observations. But the equation sounds absolutely logical.
We may indeed assume, that the higher M1 and/or M2 are, the larger the Force will be.
Also, if the distance increases, we may expect that the Force will decrease, which is accounted for by "r
" in the denominator of the equation. So, the equation "looks" sound enough.
In Newton's framework, it is indeed so that the Force that M1 exerts on M2, is exactly the same
as M2 exerts on M1.
If you look at the Solar system, the mass of the Sun is so large, that the Planets orbit the Sun.
You can use Newton's equation for calculations involving the Sun and Planets, or sattelites orbiting Earth etc..
Example:
Here is an example. Suppose a Person of 70kg is at the surface of Earth. What is the force that the Earth excerts on this person
(and ofcourse the other way around)?
If we take:
G = 6.673 * 10-11 N m2/kg2, r=6.38 x 106 m (radius Earth), M1 =70kg, M2=6*1024 kg (mass Earth),
Then we have:
| F = | 6.673 * 10-11 |
70 * 6*1024 -------------- (6.38 x 106)2 |
which is about 688 N.
6.2. Gravitational potential energy.
If two masses are (relatively) close, one can address the Gravitational potential energy of one systemin the gravitational field of the other system.
Usually, one system (M1) is substantially smaller than the other (M2), like a Planet in the field of a Star, or
a sattelite in the gravitational field of Earth etc..
Suppose, the distance between the objects is "r". Then the potential Energy of M1 is:
| Epot, M1 = | - G |
M1 * M2 -------- r |
You may have two questions. Why the "-" sign, and what happened to the quadratic power of "r"?
To start with the latter: You know that W = F * s. So, Energy is equal to Force x Distance.
The Force has a quadratic term in the denominator, and we have a multiplication with "distance" (r),
which leads to the equation shown above.
I immediately admit that this is a bit of a "Jip and Janneke" explanation.
Better is, to review the amount of work needed, to bring an object of mass M1, located at infinity,
thus where it's potential Energy with respect to M2 must be "0", and then move it nearer and nearer,
all the way up to distance "r" from Mq2. This is an integral, and it looks a bit like:
Work of F from infinity to r = |
∫infr G |
M1 * M2
|
dr |
If you know math, then you might know that the primitive of r-2, is -r-1,
which then explains the formula of the gravitational potential, and the negative sign.
However, if you are like me, the negative sign is not explained adequately enough.
Ok...
If I would say that only relative values matter, you might start laughing, although it's really so.
I mean, the temp difference between 1000K and 1100K, is not different as in 10000K and 10100K.
But as you carry a brik upwards a tower, it's potential energy might increase from 0 to e.g. 100 J.
Indeed, the higher the altitude, the more positive the potential energy becomes. Yes? Yes.
But that's the same as if it would increase from -300 J to -200 J, which is a positive increment of +100 J.
But in Highshool questions/tasks, it is often presented as being absolute values. Ofcourse, if we take
a brick upwards a tower, it's potential energy goes up with 100 J.
If we then let it fall, Ekin will go up and Epot will go down.
Falling at the ground, Epot is zero, and Ekin reached it's maximum (Ekin in value, was just what Epot was at the top).
Now, suppose, you discover a hole in the ground. It's 100m deep. It seems that the ground the brick is on,
is not Epot=0, since you can drop the brick into the hole.
So, it's a bit arbitrary, in the sense that absolute values are often meaningless, but differences
(in height, and thus in Epot), do matter.
For about the gravitational potential, for which we can see the formula above:
- As r increases, so does Epot, although it gets less negative. It seems correct.
- As r is very, very large, two masses M1 and M2 are disconected in any way,
so it makes sense that Epot nears zero.
- Mathematically, we simply arrive at the formula about, which describes the behaviour of Epot.
Since Epot, M1 resembles a y= - 1/x function (since r is in the denominator), a rough
graph of Epot, M1 is shown below.
At a larger distances, Epot, M1 is getting nearer and nearer to "0".
Figure 15.

Keep in mind that the sketch above, is no more than a graphical represention of the formula
for Epot, as derived above.
For n illustrative example, see exercise 5 below.
6.3. The escape velocity.
What velocity do you need, to "just" escape the gravity of a larger mass? In such cases, we assume that theobject that needs to escape (like a rocket), must have a minimal energy, or a minimal speed,
to "just" get out of the attractive gravitational field (the force) of a large mass (like a planet as
Jupiter, Mars, Earth, or any other larger mass).
It's the "minimum" speed, so, at a large enough distance, the speed may even go to "near 0".
And Ekin is going to 0 as well. So, we are looking for that minimum amount of speed (or energy).
Usually, one calculates that, when the smaller object (the rocket) is on the surface of the larger mass,
but it may also already be in orbit (although then obviously the numbers will be different).
There are several approaches to find the escape velocity. We know the expression for the "centripal Force",
as was shown in equation 29. You can equal that to the gravitational force, as shown above.
With a bit of rearrangements, you can find the formula.
It's even easier to use an energy balance. We can write down the general equation for the initial kinetic energy
required, and equal that to the potential energy. The total energy at the start (on the surface) is 0,
that is, Ekin + Epot = 0. So:
| ½ m * vesc2 | + | - G |
m * M ----- r |
= 0 |
So:
| ½ m * vesc2 | = | G |
m * M ----- r |
On both sides of the equation, we have "m", so we can eliminate that. It's amazing that we can do that,
because then it turns out that vesc is independant of "m". That's amazing. Did you expect that?
| ½ vesc2 | = | G |
M -- r |
From here, it is quite easy to find that:
| vesc | = | √ ( |
2GM ---- r |
) |
Additional exercises:
Exercise 1:
Suppose we have a track in the form of a circle. A small ball of 31 gramis mounted at the top. The radius of the track is 42 cm.
The angle α is 50 degrees.
At t=0, we release the ball, and the ball leaves the track at point C.
You may neglect any form of friction.
See the figure below.

1. What is the amount of work which gravity performed up to point C ?
2. Suppose the track delivers 2.5 N of force Fw due to friction.
Which total amount of work is performed by Fw?
3. What is the velocity of the ball at point C (no friction) ?
Part 1.
At the top, Ep + Ek = mgh + 0 = 0.031*0.42*9.81 = 0.128 J
At the bottom Ep + Ek = 0 + ½mv2 = 0.128 J
The above facts are nice to know, but we can do the calculation as follows:
We only need the height difference between A and C. This way, we can find Ep,
which will is exactly the positive amount of work performed by gravity.
cos(α) = MX/MC.
cos(50) = MX/MC
0.643 = MX /0.42 => MX= 0.643 * 0.42 = 0.27 m.
=> XB = 0.42-0.27= 0.15.
Ep at height X = 0.15 * 0.031 * 9.81 = 0.045 J. This amount is "negative".
Ep difference point A to X = 0.128 - 0.045 = 0.083 J = 8.3 * 10-2
The work done by gravity at point C is netto 8.3 * 10-2 J.
Can it be analyzed in a much simpler fashion?
You only need to know the height difference between A and C.
Ep=W=mgh=m * g * r*sin(90-40) = 0.031 * 9.81 * (0.42 * sin(90-40)) = 8.3 * 10-2 J.
Part 2.
We need to know the length of the arc ABC. Call this length "S".
Then we can apply W = F * S.
Circumference circle = 2 * π * r = 2 * π * 0.42.
The arc ABC is the part (90+50) degrees / 360 degrees of the total Circumference circle.
S = 2 * π * 0.42 * (140/360) = 1.02m.
W = 2.5 * 1.02 = 2.55 J.
Part 3.
Try this yourself.
Exercise 2:
Suppose a Person of 70kg is at the surface of Earth. What is the force that the Earth excerts on this person(and ofcourse the other way around)?
We must use:
| F = | G |
M1 * M2 -------- r2 |
If we take:
G = 6.673 * 10-11 N m2/kg2,
r=6.38 x 106 m (radius Earth),
M1 =70kg,
M2=6*1024 kg (mass Earth),
Then we have:
| F = | 6.673 * 10-11 |
70 * 6*1024 -------------- (6.38 x 106)2 |
which is about 688 N.
Exercise 3:
A steel bal rests on the floor. Someone, with hammer, hits the bal, and this ballrolls along a road, untill it slowly stops due to friction.
- The ball is 1.5kg.
- The distance "d" covered is 25m, before it comes to rest.
- The force of Friction Fw is 15 N.
What was the initial velocity, immediately after the hammer hits this ball?
½ m v2 = Fw * d
½ 1.5 v2 = 15 * 25
v2 = (15 * 25) * 2 / 1.5 = 500 => v= √500 m/s (is about 22.4 m/s)
Exercise 4:
At t=0, an object is traveling with a constnt speed of 10 m/s.At the same time, an unknown but constant friction sets in, and after 10 seconds,
the object comes to a halt.
See the figure below.

What is the distance S covered by the object?
There are multiple ways to calculate this:
Method 1.
The initial speed = 10 m/s. The end speed is 0 m/s.
So, the average speed is 5 m/s.
S = vaverage * t = 5 * 10 = 50m.
Method 2.
S = v * t.
Just like with a rectangular, the Surface is length * height. This principle works here too.
So, calculate the Surface of the triangle:
S = ½ * v * t = ½ * 10 * 10 = 50.
Question: Are you happy with the shape of the function, which is a line?
Yes. It's a constant accelertion or decelleration, so v=at is a linear function of "t", and a is constant.
Here we would have:
v(t) = v0 + at
v(t) = 10 + at (in this case, a is negative).
Would you be able to calculate the decelleration?
0 = 10 + a * 10 => a * 10 = -10 => a = -1 m/s2.
Exercise 5: Gravitational potential energy.
Suppose, on the surface of Earth, we have a payload of 400kg, which we must liftto the International Space Station ISS.
This example, does not illustrate a rocket launch, because a rocket must develop a high
kinetic energy, or speed, to be able to stay in orbit around the Earth.
So, this example deals with gravitational energy only.
The ISS is about 450km above Earth. The Earth has a certain radius, and the ISS has a radius
of it's orbit which is 450 km larger.
G = 6.673 * 10-11 N m2/kg2
m: Mass payload: 400kg
ME: Mass Earth: 5.96 * 1024kg
rEarth=6.37*106m = 6370000m
rorbit = rEarth + 450000m=6370000m + 450000m = 6820000m
| Δ Epot | = | Epot, orbit - Epot, Earth | = |
-G*ME*m -------------- rorbit |
- |
-G*ME*m -------------- rEarth |
It's quite a calculation, and I leave it up to you.
But you should arrive at a positive number.