Some basics of "Theories of Parallel Universes", in a very simple note.
Date : 03/08/2018
Version: 0.9
By: Albert van der Sel
Status: Ready. But it remains a Working document: Subjects will be added when needed.
Remark: Please refresh the page to see any updates.
Some theories from Physics on Parallel Universes.
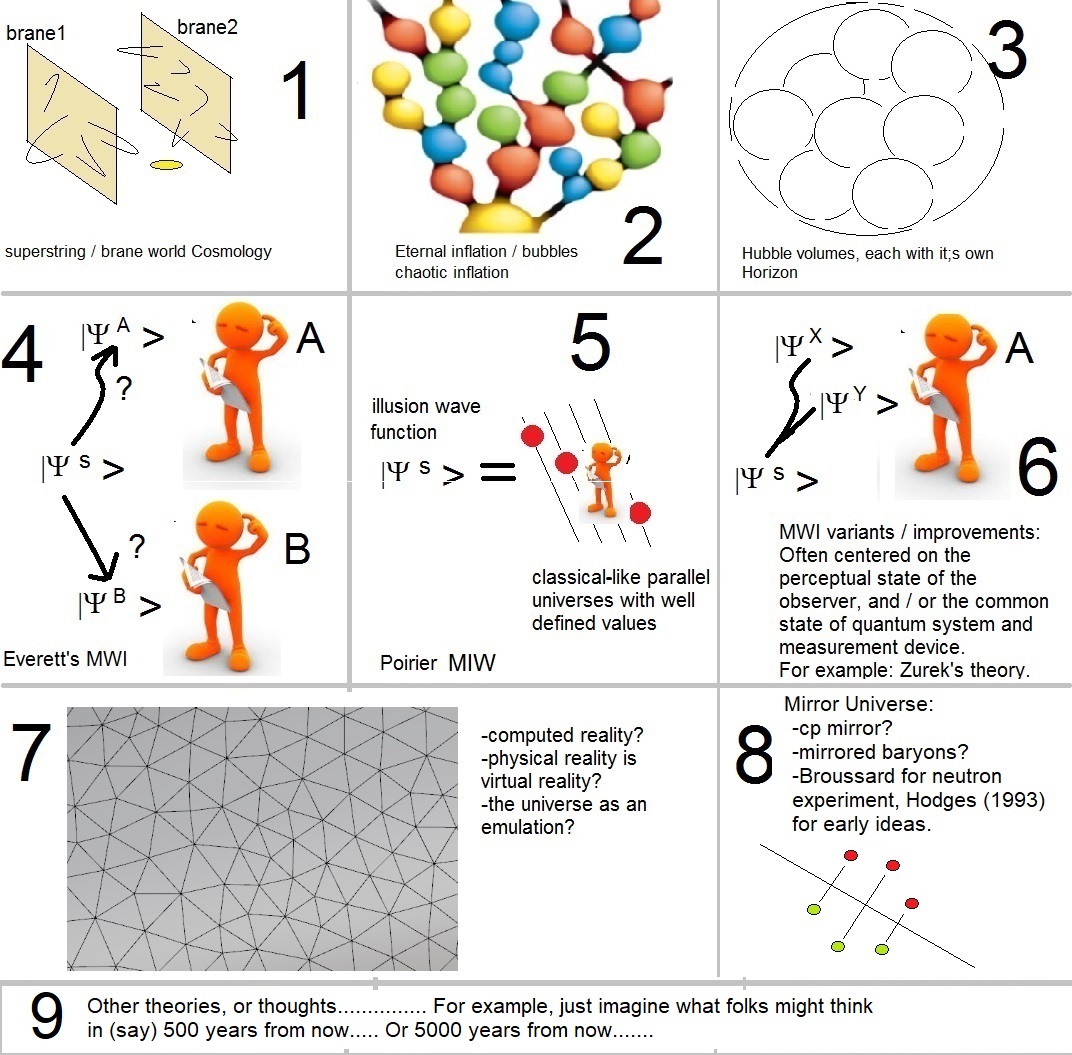
Fig. 1: Here, 7 approaches are shown in simple pictorial figures.
It's true that at least 7 or 8 "ideas"/"models" exists, from which it follows that the existence of parallel universes
might be possible. Here, a few originate from "interpretations" of Quantum Mechanics, while some others have emerged
from theoretical physics and cosmological models.
Let's take a brief look what on they are about... Maybe you even like it!
Just for the record... there is nothing "hazy" here, since they all are real ideas from Physics.
However, most ideas are considered only by limited number of physicists.
Indeed, it is fair to say that probably a minority of physicists accept Parallel Universes, as a "solution"
for a number of certain observations (later more on that).
Even if you are a "supporter": we simply have no truly conclusive "evidence" that one of them is on the right track.
Indeed: no real, solid, pointer at all. However, maybe some pointers will be found sometime from now, possibly through experiments.
However, the general idea among physicists is, that some ideas are a bit stronger compared to others.
But that still varies a bit over time. For example, I always thought that support for "Everett's MWI theory (1957)" (see below)
declined during the '80's/90's, but it still amazes me how many articles still keep appearing, in favour of Everett's idea's
or derivates of those idea's.
Also, as another model, "Poirier's MIW theory (2012)" seems rather tight, but at the same time I never could find
many supporters for this theory.
It's not impossible that experiments performed in the coming years will make a point for a certain theory.
For example, some Cosmological Brane-world scenario's also predict certain particles/fields (undetected up to now, e.g. "branons"),
that are in line with Brane-world scenario's. It's not impossible that future LHC experiments will provide
some clues for the existence of such particles/fields.
By the way: The LHC is currently the world's largest particle acclerator.
In a discussion about SpaceTime, a review of "Parallel World" theories, is absolutely justified.
So, let's see what we are dealing with...
I simply randomly picked a theory to start with, and I will gradually work (briefly) through all of them.
Let's start with the older "Everett's MWI" theory.
REMARK: I certainly do not say that the overview presented in this note, is complete.
Far from it. But, it should cover some mainstream lines of thought.
However, as to be expected from science, new- (or revived older-) "contours" come up all the time.
Some of those newer thoughts are not included yet in this simple note.
Also, as you will notice, a clean and rigorous mathematical treatment is absent in this simple note.
Personally, I am not especially "pro" for any of such theories covering "Parallel Worlds".
However, some theories seem to be quite waterproof, and kept physicists busy for decades.
And the subject is quite facinating...
I am not sure if I am doing a good job here. Just let me try.
Main Contents:
1. Everett's "Many Worlds Interpretation MWI" (1957).
2. Hubble Volumes.
3. Poirier's theory of interfering "classical" universes (MIW).
4. Inflation with bubbles / eternal inflation / chaotic Inflation.
5. The Universe as an emulation, or "physical reality=virtual reality".
6. Brane - World Cosmology.
7. Proposed tests, using Quantum Mechanics and Quantum Computing.
8. The "Many Minds" theory.
1. Everett's "Many Worlds Interpretation MWI" (1957).
A great physicist once said: "Nobody understands Quantum Mechanics".
Ofcourse we might be able to apply the rules of a certain mathematical framework, but that does not mean
we truly understand what is really behind it. So, many wonder on how we must interpret Quantum Mechanics (QM).
Even today, there still is no absolute answer. At least, the following important interpretations exists:
Table 1:
-The Copenhagen interpretation.
-QM with Hidden variables.
-Decoherence as a successor to the Copenhagen "collapse".
-Everett's Many Worlds Interpretation (MWI) -a multiverse theory.
-The Many Minds Interpretation -a "light" multiverse/multimind theory.
-Poirier's "Waveless" Classical Interpretation (MIW) -a multiverse theory.
-The transactional interpretation.
-de Broglie - Bohm "Pilot Wave" Interpretation (PWI).
-possibly also the "Two State Vector Formalism".
As you can see from the listing above, Everett's "Many Worlds Interpretation MWI" is a well-known interpretation of QM.
It's a remarkable long listing indeed. If you would like a brief and very simple overview on most of those interpretations first,
you might like to see this note.
That's one of my notes, so it certainly is not "great" or something, but at least it's short (and hopefully not too boring).
In this section, we will briefly focus on Everett's (and Wheeler's) "Many Worlds Interpretation" (MWI).
It stems from around 1957, and it is indeed a true Parallel Universe Theory. As from the first appearence of
the article, it needed a couple of years "to sink in" in the community of physicists.
The way I see it, from around 1965 to about 1985, it was a very serious competitive theory amongst all other
interpretations. I would say, that in it's "best years", probably over 30% of physicists gave it serious thought
and a relevant fraction of those physicists even believed it was the best we had.
A mechanism called Quantum Decoherence, was first formulated by Zeh, around 1970. This was a good alternative
for the "strange" collapse of the statevector, as is formulated in the Copenhagen interpretation.
Initially, in the early '70's, it seemed that decoherence did not land smoothly in the community.
However, from (about) 1990, Zurek gave new momentum to Decoherence, and Copenhagen and also MWI, lost popularity. Even without
considering Zeh/Zurek's "decohrence" paradigm, many scientists gradually discovered more and more, that MWI lacked
a true "oncology", and that it actually focussed too much on an objective "wave function" (or statevector) itself.
I would say, that from around 1995 (or so), more and more studies appeared which all made it quite likely that
it's really difficult to sustain MWI as one of the best candidates anymore, and that it even might be flawed,
but the latter was (probably) never really proven.
I must however hastely add that MWI still has a certain base of supporting scientists.
To make that a bit stronger: regularly (even today) new articles are published which makes a case for the MWI theory,
so, if I made the suggestion that MWI is "nearly dead", this is by no means true.
However, the supporting base of physicists supporting MWI, seems to be decreasing, since, say, 1990 or so.
The "orthodox" interpretations in QM, like the Copenhagen view.
There is no such thing as "orthodox" QM, but I need some means to distinguish between the "traditional ways"
to look at QM, like the Copenhagen Interpretation, or Hidden variables, and the ways to treat QM
in the context of parallel universes. Therefore, theories which explicitly uses parallel universes or "many worlds",
I would like to call "non-orthodox" interpretations of QM, in this note.
Ofcourse, it's quite hard to sustain that a theory like the "pilot-wave" (of de Broglie-Bohm) is really "orthodox", since
it's certainly not. However, it does not refer to "Many worlds". So, I hope you get my idea here.
So, let's first take a quick look at a typical orthodox description:
Let's suppose we have a fictitious Quantum System that we can represent by a "vector" (or State vector).
|Ψ>= a |BOX1> + b |BOX2> + c |BOX3> (equation 1)
This fictitious Quantum System (say the position of a particle), is a superposition of the three different states
|BOX1>, |BOX2> and |BOX3>, meaning..., yeah... Meaning what?
In the Copenhagen interpretation it is said that there is a chance that when a measurement takes place, we may
find the particle either in BOX1, or BOX2, or BOX3, with probabilities for which hold |a|2 + |b|2 + |c|2=1
The latter equation is not strange, since all probabilities must add to 1 (or 100%).
But equation 1 is strange. Does it mean, before we performed any measurement, that the position of the particle
is in BOX1, and BOX2, and BOX3 simultaneously?
Yes, indeed. This is very strange, since we have no classical equivalent for something like this.
However, for example the QM solutions for the position of an electron in a Hydrogen atom, is quite similar to what we have above.
This is called the "superposition principle".
But here we have a measurement problem. The moment you open the boxes, and say, you find the particle in BOX3, then what
happened to the superpostion (as expressed in equation 1) ?
The Copenhagen interpretation now postulates that the Statevector (like equation 1) "collapses" into one
of it's basis states, like |BOX3> (also called "eigen" states).
Here we have a real problem in QM, and facts like this one, triggered lots of people to ponder on how to interpret QM.
Most notably, in the twenties, thirties of the former century, there was quite some opposition to the Copenhagen view.
However, some of the people who favoured it, quite often saw it as just a "working" methodology, since it worked.
But, many were not happy at all, and for instance Einstein proposed that QM is "not complete".
It also lead somewhat later to the postulate of "Hidden Variables", that is, variables we do not know yet, but if we would known them,
it would remove all "vaque-ness" and made QM deterministic again.
By the way, in table 1, you can see quite some alternatives for the Copenhagen interpretation, like for example the "Pilot Wave"
interpretation of de Broglie, which was leter picked up by Bohm again.
Or explaining Quantum phenomena using the idea of "hidden variables", in such a way, that if those variables were know,
we would have a deterministic theory again.
By the way, equation 1 shows a statevector which is expanded in 3 basisstates. In general, when dealing with "n" dimensions
with respect to the number of basisstates, we have:
|Ψ > = c1|a1 >+ c2|a2 >+...+ cn|an > = Σ ci |ai > (equation 2)
In QM, people often speak of a complex "Hilbert space" where |Ψ > is member of.
A little more on "superposition":
The interpretation of "Superposition" in QM, is still a subject of debate, starting from the very first concept
of the idea in the early days of QM, all the way up to today.
When you see an equation as something like:
|Ψ >= α |0> + β |1>
where |0> and |1> are "basic" vectors, it looks like a simple vector superposition.
But, something weird is going on. We only know that |Ψ > is |Ψ >.
Only when a measurement on the observable (which |Ψ > represents) is done, we will find
either |0> or |1>. The corresponding probabilities for finding such basic state (eigenstate), must adhere
to the relation |α|2 + |β|2 = 1, because the sum of all probabilities
must add up to "1".
The phrase "only when a measurement is done, we will find one of the eigenstates", is amazing.
Suppose you find the state |1>, then what happened with |0>?
So, what is this? Does |Ψ > collapses into one of it's basis states (eigen vectors), or is it
the principle of decoherence which is at work here? Indeed, the "measurement problem" is key in
all interpretations of QM.
As another thing: Many physicists accept the idea that, unmeasured (or unobserved), |Ψ > written as
|Ψ >= α|0> + β|1> means that |Ψ > "exists" as |0> and |1> at the same time.
However, such an idea introduces it's own difficulties.
Even in such simple discussion as we see here, it's not too strange that the seemingly intrinsic
probabilistic behaviour we see in QM, might lead to idea's of "parallel universes".
That is: at an observation of |Ψ >, you might found |0>, but you might also have found the state |1>.
So, why not rephrase the matters like this: In one Universe you found |0>, and in another you found |1>.
The real theories dealing which such interpretations are ocourse much more delicate and rigourous than my
extremely simplistic example scetched above. Such theories really have substance, as you will see below.
However, I personally am not a proponent of any one of them. But it is facinating stuff for sure.
Everett's Many Worlds Interpretation (MWI) of QM:
Around 1957, Everett published his Phd thesis, "Relative State Formulation of Quantum Mechanics", which was more or less
the Grandmother of parallel universe Theories in QM. Slightly later, folks started to call it "The Many World Interpretation".
In short: The Many-Worlds Interpretation of QM holds that there are many worlds which exist in parallel in the same SpaceTime
where you are part of. In many cases, where Copenhagen would talk of the (strange) collapse at a measurement, in MWI
the current Universe "forks" into new chains of events. In a sense, the Theory is "deterministic" if the mechanics of how
the "forks" work, would be well explained.
Please note that Everett's original arcticle was called "Relative State Formulation of Quantum Mechanics", so for
Everett, an absolute state does not exist, and we are always dealing with "relative states".
Everett used the original "wave function" description of QM. Although equations like equation 1, resembles a "vector notation",
the wave function decription is very similar (or equivalent). It is like as if you would "superpose" a number of sine or cosine functions,
all with a different "mode" n. If you would then apply it to describe the position or momentum of a particle, you get
a sort of wave packet with a maximum Amplitude at it's centre, and with less amplitude at the "fringes".
Here too, a certain wavefunction which is part of the superposition, might be regarded as an eigenstate, just like we did above.
Such a description would make the position of a particle very "localized", but not exactly localized, unless
you perform a measurement of the position.
This is a view of a superpostion of wavefunctions. Now, you may ask what happens if you introduces some sort of
measuring device. Is it possible that the composite wavefunctions could individually interact with such device?
It turns out that it is not easy to formulate it this way.
But Everett, in a way, reasoned along such lines.
Using a view of composite systems like a Quantum System and measuring devices, he shows that a "jump" to an eigenstate
is relative upon the mode of decomposition of the total wave function into the superposition, which actually means that any found
result state is "simply relative". He further shows that such a process is continuous, and thus will not stop.
In other words, the substates in the wavefunction can independently interact with the environment (like doing a measurement),
and they "fork off" and evolve independently.
This would explain why Albert finds a certain quantum result in an experiment, while Mary finds another.
A reader might note, that as a main collary of Everett's work, is that the Universe might be percieved
as a Multi-verse of branched-off "Worlds".
Everett himself, further never refers to parallel universes or something similar in his original text.
For him, the key words are "relative states" and "splitting in branches".
Although this already "almost" forces one to reason in terms of "Many Worlds", such label did not came from Everett himself.
Everetts formalism was slightly later called a "Many Worlds" theory, by others, and that "label" sort of kept stuck.
The original article is truly a "classic" in QM.
It is further extremely interesting that there really exists a "pre-seed" for "decoherence" in Everett's theory.
This is more for historians to investigate further.
Simple pictorial description of Everett's MWI:
If you did not liked the discussion above, I have a simple, very short (but a bit flawed), pictorial description of MWI:
In a simple pictorial representation: Suppose we have a particle, and let's represent it by a "coin".
Ofcourse, this coin can be expanded in sub-coins (or basis coins), just like equation 2 above shows us.
So, our coin is a "superposition" (like, for example, 1 euro is 10 x 10 cents, or 5 x 20 cents).
MWI acts like having that coin (the superposition), which is a large set of (sub-) coins (the subwaves),
and when you throw them away, they all roll into different directions, all acting differently with their own parts
of the environment.
Every such sub-coin, is now branched off into it's own "world".
Ofcourse, we need a bit imagination here, and just think that all those "private" parts of the environment,
which interacted with the nth (sub) coin, is now completely detached from the other parts of the environment.
(Allright, it's not great, but it's no more than just a humble attempt... I understand, if you don't like this too).
2. Hubble Volumes.
This time we go for the very.. very large...
I wonder in how much you will appreciate this section as a "Theory of parallel universes", but a fact is,
that some folks indeed do so.
Although I will refer sometimes to "Inflation" in this section, "Inflation" is so interesting that I like to.
discuss it in another chapter more thoroughly.
Even in the early years of the former century, it was theoretically made plausible (Friedmann), that the Universe
was expanding. Ofcourse, that was already implied by the GTR equations of Einstein, however, Einstein rewrote
his equations in order to have a steady state Universe, which was the dominant view in the twenties.
Somewhat later, Observational proof of the epansion became really solid, when Hubble presented his "redshift" findings,
which made a real case for an expanding Universe: it seems to get larger all the time.
Well, you may wonder if that last sentence is a "good phrase" anyway. Reality maybe somewhat more complex.
The "history of science" is so much fun to study, but I have to stick to the real point of this section.
It is quite certain that from around 1950 (or so), it was mostly accepted that we have to deal with an
expanding Universe. That is, starsystems like remote galaxies seem to recede from us, and a peculiar thing is that they
seem to recede faster, the larger the distance is (from us).
For the larger part of the second half of the former century, questions remained like, for eaxmple, will the expansion
slowly decellerate at some point. Or, is it possible that the expansion comes to a halt, and that the Universe will undergo
a Big Crunch again? Or will it simply expand forever...?
Many of such questions were alive among cosmologists, and important pointers were under study like the "mass-energy"
distribution, and, for example, if SpaceTime was curved on a large scale etc...
At some point, folks started to realize that the "seemingly" enormous velocity of very remote systems, may have
a completely different origin. The velocities were based on the large "redshift" of the light of those remote systems,
just like the doppler effect for moving objects. However, the same effect occurs if space is created along
any direction. You probably know that famous example of a baloon, with dots on the surface (representing galaxies).
When you inflate the balloon, all dots recede from each other, due to the fact that the balloon's surface expands.
Something similar seems to be the case in our 4-dimensional SpaceTime.
Even at this "point", using the theory sofar, it makes sense to investigate the "horizon", or "Hubble volume".
But we can even put some more fire into the discussion on expansion.
Accelerated expansion:
Around 1998, a rather comprehensive study started, to measure luminosities of several "Type Ia supernova's"
which are "exploding" stars, but which have proven to be very accurate "candles" with a very definite luminosity.
They can be very useful to determine "distance/redshift" relations.
After sufficient data was accumulated, interpretations seem to suggest that the luminosity of more remote supernova
were actually (and this is the crux) dimmer and more redshifted than expected.
Ofcourse, the actual techniques are much more involved, but typically, the results are often shown in graphs which show
the observed magnitudes plotted against the (socalled) redshift parameter z.
The plots thus aquired, seem to suggest an accelerated expansion, instead of a expansion which slowly decreases.
So, at this moment, most astronomers and cosmologists believe that the Universe undergoes an accelerated expansion.
The source which drives that expansion still puzzles many physicists and cosmologists.
Several candidates were forwarded, as for example an intrinsic pressure in the Vacuum, or an still unknown field
called "quintessence", or possibly some other source.
In general, the still unknown agent behind it, is collectively labeled as "Dark Energy".
However, the Cosmological Constant (which Einstein introduced in his field equations), might be a good candidate
for being responsible for "Dark Energy".
While SpaceTime expands everywhere, for our local part of the Galaxy, there thus exists an event horizon
which is that distance from us, so that light (or information) from still more remote places, cannot reach us anymore.
There simply is too much expanding Space between us and this "event horizon".
Light, which travels at a constant velocity, cannot overcome the ever increasing/expanding Space anymore, as from
a certain distance.
In effect, this 'event horizon' defines a "region" (similar to a sphere), which is called a "Hubble Volume".
For anything beyond that horizon, we cannot receive information.
Some people also say that we actually dealing with "causal disconnected regions".
Also, some rephrase that as that we are living in our own "patch of the full Universe".
But, what is the connection with "parallel universes" or the "multiverse"?
Above it was made likely, that we are in our own "patch" of the Universe, or Hubble volume, which is bounded by
an event horizon. Beyond the horizon, given the data and observations we have today, similar conditions would apply.
Hence, far beyound our Horizon, it would be likely that at those places we have similar SpaceTime with the usual
"content" as we have "here" (Galaxies, clusters etc..). However, those far places are fully out of reach (even for light,
or any other forms of information exchange), and thus some folks talk about a "multiverse" or "parallel universes".
The fact that each Hubble volume has it's own "cutoff" for all possible other Hubble volumes, make that some folks
place this in the "Parallel Universe" (or multiverse) category.
Whether you would also consider this to be a Multi-verse (Multiple Universes) Theory, is fully up to you.
But some folks really do so.
3. Poirier's theory of interfering "classical" universes (MIW).
The seemingly "probabilistic" behaviour of quantum obervables, might be due to an idea nowadays
called the "Many Interacting Worlds (MIW)" theory.
The "Many Interacting Worlds (MIW)" theory, is fully different from Everett's "Many Worlds Interpretation (MWI)".
The QM model devised by Poirier, originated somewhere around 2010 and went through further elaboration,
especially in cooperation with Schiff, and ended in about 2012 in something what's now called MIW.
I must say, that at this time (and it might seem a bit strange), it's not fully clear to me who first re-introduced
almost classical Physics into the dicussion of "interpretations of QM", and who actually introduced MIW.
Ofcourse, I have to say quickly that the Broglie-Bohm (pilot wave) interpretation uses many classical features as well.
However, in MIW, it truly goes one step further since each independend "world" in MIW, is fully ruled by classical physics.
This will be explained below.
About the origins of MIW:
It seems that Holland, Hall, and several others, do or did rather similar work as Poirier.
But, someone like Sebens also recently launced similar ideas as MIW.
But they all operate closely in the same "arena", and since most scientists seem to attribute MIW
to Poirier, from now on I will take that as a fact.
A core idea in Porier's Theory is, that multiple classical Universes exist. For example, a particle has
a well-defined position in such classical Universe. The point is, that all those Universes are slightly
different in their "configuration spaces" (see below), and also interacting with each other.
As such, we experience "the illusion" of Quantum probabilities.
In this way, a measurement may give rise to some result, while the same measurement a little later,
might produce another result (like the spin Up, or spin Down of some elementary particle).
Also, in reality, there exists no Wavefunction, or vectors written as an expansion of basis states.
It only "seems" that way, but reality is different, namely multiple interacting Classical Universes.
Considering the basics of the "Many Interacting Worlds" theory, You might see a parallel (no pun indended) to Everett's
"Many Worlds Interpretation" (MWI), but that would not be correct.
There are fundamental differences. Most notably:
- In Everett's MWI, the wave function is real and plays a central role. In MIW, the wave function does not exist,
and in fact MIW is a sort of QM "without the wavefunction".
- In Everett's MWI, universes branches off due to the fact that superimposed waves each interact with the environment.
In Poirier's MIW, there is no branching, no wavefunctions, but the many worlds may "interact".
- Everett's MWI uses standard Quantum Mechanics (wavefunctions, probabilities etc..), however Poirier uses established
rules from many parts of physics, whereas many are simply familiar classical, like trajectories, position/impuls, Lagrangian etc..,
where paths over different trajectories relate to the Many Interacting Worlds.
Most striking thus, is that in MIW, the Wave function with all its superimposed waves (states) is actually non-existent (!)
It's more an illusion, due to the fact that in Poirier's "Many Worlds", an observable might have
well-defined values in different "Worlds", that is, each "World" it has it's own "private" values for that observable,
but since there exists variation between "Worlds", we percieve the illusion of a composed State vector where the same
experiment might show different values all the time.
So, if you like, you might say that there is no fuzziness in Poirier's theory: for example, particles do occupy well-defined
positions in any given world. However, these positions vary from world to world, and thus explaining why they appear
to be in several places at once. That we observe that, is due to the fact that (according to MIW), nearby "Worlds" interact.
It's that same interaction which makes us believe in the spreading of wavepackets and for example tunneling through a potential barrier.
In MIW, each world evolves according to classical Newtonian physics. All (illusionary) quantum effects arise from, and only from,
the interaction between worlds.
What are the "Worlds" in Everett's MWI and Poirier's MIW?
In MWI, it's not too hard. Everett only talks of "relative states", and the branching occurs when the superimposed waves
interact differently with the waves of the environment. Although quantum probabilities still hold, another key element of which
we must bee aware of, is that if SubstateA has a certain propbability, and SubstateB has a another probability,
each can "branch off" at interaction, and start a "life" by their own. Think of them as initially as orthogonal, and start their own
different projected life in the environment (where that microscopic environment is affected too ofcourse).
It's like having a coin (the superposition), which is a large set of (smaller) coins (the subwaves), and when you throw them away,
they all roll into different directions, acting differently with the environment.
In MIW it's a tiny bit more delicate.
A rather simple way is to take an aspect of the "Broglie - Bohm" (pilot wave-) interpretation as a starting point.
If you would have "n" particles, then you might define one "configuration space" for that set of particles, which space
can be described by the vector:
{q1,q2,...qm} (equation 3)
where m is larger than "n" since we might review our particles in several dimensions, like 1, or 2, or 3 (like our normal 3D distance space).
It's important to keep in mind here, that we here use one configuration space for those "n" particles.
When physicists work out such a model, then positions, and momentum, and other characteristics of the particles can be described
in such a framework.
The rather "bold" assumption in MIW is, that not only one "configuration space" might be possible, but say "J" seperate spaces,
where J might even go to infinity. That's rather new, to say the least. Now we have "J" spaces, where each "j" in J, defines
a configuration space, where each one "j" describes all the positions and momenta of those "n" particles.
Thus we might have:
{p1,p2,...pm} (set 1)
{q1,q2,...qm} (set 2)
..
..
{y1,y2,...ym} (set J) (equation 4)
Those sets, namely {set 1} up to {set J}, then defines the "J" parallel Worlds, since each set describes the
the full configuration space (e.g. positions, momenta etc..) of "n" particles (or all particles).
-So, suppose we have just one particular j=j1, then we have a certain "configuration space", descrbing the positions
and momenta of "n" particles, like for example {p1,p2,...pm}.
-And, suppose we have j=j2, then we have another "configuration space", descrbing the positions
and momenta of the same "n" particles, like for example {q1,q2,...qm}, but in effect
with different positions and momenta compared to j=j1
Did you noticed for example the different positions for j=j1 and j=j2 (and all other "j" from J)?
When physicists further work out such a model, then positions, and momentum, and other characteristics of the particles
described by one "j", like j=j1, might be affected by characteristics of the particles from another configuration space,
like j=j2.
It can be further made likely, (using some math) that "close" "j" from the space of J "configuration spaces", tend to work
repulsive, so that the illusion is created that, for example, we are dealing with a spreaded wavepacket as a particle.
I hope this conveys at least a "glimse" of the heart of MIW. Actually, you might say that MIW turned QM around to be classical again.
It's a rather elaborate Theory. Most phenomena from QM, like for example the double slit experiment, or
typical Quantum effects like "tunneling", is handled in this new Classical approach.
4. Inflation with bubbles / eternal inflation / chaotic Inflation.
It's probably hard to believe that "an awful lot", (that is, the Universe), can come from "nothing" (or from "almost nothing").
The following has not much to do with inflation, but we may take a short excursion to one of the Heisenberg
uncertainty relations, which is a remarkable fact in QM.
The particular relation I am talking about, describes an uncertainty in "Energy" and "Time".
The relation say that in the microscopic domain, energy can be obtained from the vacuum as long
as the following holds: ΔE.Δt ≥ ħ/2 (where E is Energy, and T is time).
So, you can borrow energy for a certain timeslot, as long as it is returned later on, according to the relation.
The socalled microscopic "quantum fluctuations" are believed to exist literally everywhere in our present SpaceTime.
One such manifestation are the "virtual particles", which popup from the Vacuum, and destroy each other again, only
existing for a very brief moment.
The section above, has the advantage that we now are introduced to the concept of "quantum fluctuation",
in case you was not aware of it.
As of around January 1980, Alan Guth started talking openly on his new ideas of the origin of the Univere.
Then, in January 1981, a (nowadays) famous article was published (Physical review D), which beared the title:
Inflationary universe: A possible solution to the horizon and flatness problems.
This theory explained the birth of the universe in a unique and completely new way, and at the same time avoiding the
problems as mentioned in the title of the article. His theory of "inflation" was pretty good in describing the most
extremely early phases (like as from 10-38 second to 10-32 second, and a tiny bit later on),
but it did not correctly handled some later phases, as Guth admitted.
However, it was already a major step from the earlier "Big Bang" proposal, which presumed a strange superdense,
superheated singularity, which for some reason, "exploded" and ultimately formed the Universe as we know it today.
However, as people see it often today, is that when the Inflationary period ends, the next phase then fits the traditional
"Big bang" well, so it is nowadays often interpreted that the Big bang follows afer Inflation.
It was only a few years later (1983) that Andrei Linde proposed a revamped approach, and actually cured
the major problems in the original theory. However, Linde's approach, actually made eternal inflation,
or a bubbled Multiverse (multiverse=multiple universes), very likely.
So, for my purpose, that's a very interesting item to discuss.
The basic idea behind Cosmic Inflation:
If there is really "nothing", then there is no space, and no time. In effect, you might say that it's useless to ask "what was before"
since, time does not exist. So, the notion of "before" is non-existent. If you like, you may visualize it as if space and time
are both spatialized, but "0".
Modern theories try to unify the known forces in our present day Universe, and also try to unify fundamental
theories (like QM and gravity). It is expected that at extremely small scales, all the fundamental theories "converge"
to each other, and thus unify. In that sense, it may well be so, that that QM effects and Gravity are then very "close".
Now, the absolute "bootstrap" of the start of Inflation is still not solved, but it is often argued that in a period
around a period of 10-42 second (or so) from "0", a quantum fluctuation occured and it entered into a precursor of gravity.
Once gravity exists, in whatever form, a certain format of Vacuum exists then too.
This extremely short period is sometimes referred to as the "Planck epoch".
Guth's theory states that this 'pre-space" is equivalent to an extremely small patch of "false vacuum" which theoretically
is the same as "negative pressure", or "positve gravity", which is a repulsive gravitational field
Note: Maybe "positive" and "negative" pressure are confusing, but pressure behaves very much like gravity.
A positive pressure namely, equates to an attractive gravitational field. A negative pressure is repulsive.
The "negative pressure" or repulsive gravitational field is the driving agent behind Inflation. The patch expands
exponentially since nothing holds it back. Secondly, since the false vacuum does not have anything to interact with,
the energy density stays the same, while the total energy increases. Inflation in that respect works like a magnifying glass.
Now, energy conservation says, that if the total energy in the patch increases, that must be equal to the "work" done
by the repulsive gravitational field, that is, the expansion itself. It seems as if "Inflation drives itself...."
Such a scenario looks, as if Inflation will never stop. There are some intracies indeed, and by the way, the number
of Inflational theories (since 1981) is quite large, each dealing with several subphases.
Guth further assumes on good grounds, that the Inflationary period itself is somewhere from 10-39 to 10-31 second.
For now, we assume (as Guth) that the false vacuum went instable, and the false vacuum energy is released by "snowing" (condensate)
elementary particles (quark-gluon soup) from the vacuum.
Generally it is understood that the change of the false vacuum to "true vacuum" (or steps in false to less false), have lead
to particle production.
This phase is sometimes referred to as the "quark epoch". We are now still only about 10-12 second from the absolute beginning.
That phase is ofcourse much more involved than my few line of text. For example, it's assumed that several forms of "symmetry breaking"
occurred, as the tempurature lowered, resulting in the basic forces as we know them today.
When the universe was about 10-6 seconds old, again, the temperature (energy) was lowered enough for quarks to bind
into hadrons (hardron epoch).
Several other phases followed, like the lepton epoch.
How complex the various phases can be, is also illustrated by the fact that once matter and anti-matter existed, but Nature
seemed to have had a slight preference (bias) for matter (instead of anti-matter).
Noteworthy is then the fact, that, a long time later, about 380000 years after the birth of the Universe, the temperature has
dropped sufficiently for leptons and protons to form (mainly) hydrogen, and at that point, the Universe became transparant for light,
or electromagnatic radiation in general. This is the source for the "relic" "Big Bang" background radiation.
The Horizon and flatness problems:
1. The Horizon problem:
It might be interesting to spend a few words on those problems, which were probably solved by Inflationary Cosmology.
The fact that our observable Universe is so large, places us for some problems, using a traditional Big Bang scenario.
Very distant regions, cannot contact other very distant regions, to exchange information, like heat, or other forms of radiation.
One problem (among other problems), is that the "relic" "Big Bang" background radiation (also called the 3K cosmic background),
is very accurately the same in all directions. In the traditional "Big Bang", this would not be the case. There would have been
considerable fluctuations.
In the Inflationary model, the initial false vacuum patch prior to the inflation, can be seen as very small
but causally connected region. In other words: uniform.
The inflationary epoch, evolved so extremely fast, that the homogenity was completely freezed, and that effect
we can still observe today in that famous uniform cosmic background radiation.
Thus, an original problem in the "full" Big Bang scenario, is often regarded as a "pro" for Inflation.
2. The Flatness problem:
The "full or original" Big Bang scenario poses another famous problem: the flatness problem.
This is usually expressed by, and related to, the "critical density" Ω, for which hold
that Ω can be "< 1", or exactly "1", or "> 1".
Suppose the actual density is denoted by ρA, and the density for which the universe would be flat, as ρF,
then the ratio Ω = ρA / ρF functions as a normalized density: the "critical" density.
Below is an simple argument, based on the traditional mass-energy in the Universe. However, how exactly "dark matter"
and "dark energy" would influence it, is a very important question. However, I stick for now to the (say) traditional view,
because I like to demonstrate how Inflation solves the flatness problem, which would otherwise arise in the traditional
Big Bang theory.
The total density of matter and energy in the Universe, determines the curvature of SpaceTime.
In most conjectures, the General Relativity Theory (GRT) of Einstein, is the basis to start from.
Friedmann found a solution for the field equations of GRT. This solution shows a relation between
the gravitational constant, the speed of light, and some other parameters, and most importantly, the "curvature parameter"
(which is a measure for the rate of curvature of SpaceTime), and the total mass-energy density.
Three models come up from the equations of GRT and Friedmann: a (spherically) closed Universe, an open Universe, or a flat Universe.
Please note that here we are talking about the "geometry of the universe", that is, the sort of curvature of SpaceTime.
The "flat universe" means that we do not have a curved SpaceTime (globally), and that would only happen when we have
"curvature parameter" (k) to be 0. In that case, the critical mass-energy density Ω would be exactly "1".
Or, formulated more accurately: the ratio of the actual density to this critical value is defined as Ω.
Sometimes, for clarity in equations, Ω is rearranged to be the factor (Ω-1 - 1).
So, flatness then means (Ω-1 - 1)=0.
If we go back to " Ω" again, thus the ratio of the actual density to the critical value,
If Ω > 1, then we obviously would have a large mass-energy density and the curvature is positive,
meaning a (spherically) closed Universe. Probably, after a certain time, the Universe might collapse.
If Ω < 1, then we would have a too small mass-energy density and the curvature is negative, meaning
hyperbolic open universe (with respect to curvature).
Now, most atronomers/cosmologists think we have a "fine-tunings" problem, since large-scale observations very strongly
points toward a flat universe. So, Ω seems to be "1", which is rather special, probably too special....
Why would it be exactly 1? Why would the Big Bang ultimately end up with this very special density, expressed
by Ω=1 ? This question is the "flatness problem".
If Inflation would solve this, then the next question is: why would Inflation "make" Ω=1?
This could be answered, if the Friedmann equation would still hold at the inflationary epoch. If so, then
mathematically it can be written as (Ω-1 -1) x total energy = Constant.
Without considering the "cosmological constant" Λ, the equation actually is:
(Ω-1 -1) ρ a2 = -3 kc2/8πG (equation 5)
Above we saw that during inflation, the total energy ρ increases exponentially. Now, the rightside of the "=" is constant,
since it only contains factors like "c" (speed of light), "G" (gravitational constant) and some others.
To let the product in the leftside of the "=", be constant, while ρ increases, then the term (Ω-1 -1)
must decrease sharply while ρ increases sharply.
If this reasoning is correct, then Inflation makes Ω nearing the value "1", thus a flat universe follows.
I must say that this line of reasoning is not without critism, but anyway it's an agrument that's often heard to explain
the observed flatness of the Universe.
Above we have seen the first Inflation version from Guth. Next we will see Linde's interpretation, where the Multiverse plays
a key role.
The Follow up by Linde (and others):
Above we saw Guth's original Cosmological Inflation theory from 1981 (in a few very simple words).
By now, quite a few additional versions have appeared, by various authors, often focussing
on subphases (cooling and re-heating several times), and/or symmetry breaking.
Or, some later articles, also try to reconcile string theories with inflation.
Some newer inflational theory variants, expect a "multiverse", or multiple universes, to be a reality.
That's ofcourse very interesting for my note.
However, those newer theories themselves, and who was, or is, working on them, and when original ideas were expressed,
and how much "overlap" exists, is by no means very transparant.
Key terms anyway, are "eternal" and "chaotic" inflation. Sometimes, from the relevant articles, they look
pretty much similar. Well, at least for me that impression arose by now.
But "eternal" and "chaotic" inflation are not similar, as you will see below.
Also in those newer inflation theories, Guth himself is active. In a few rather recent articles, he proposes an "eternal inflation"
variant as a more complete theory, compared to the old (original) one. The multiverse is a collary of his central theme.
However, Guth was not the first who explored "eternal inflation", and it seems that Steinhardt and Vilekin were proposing
such idea's around 1983.
Linde seems more involved in something he called "chaotic inflation", and here too, the multiverse is a collary
of the central theme.
Already at this place, I like to say that something that looks (at first sight) completely different, namely "(string) Brane
World cosmology", might not be so "incompatibel" with those newer inflation theories afterall, according to some authors.
I like to touch that subject (that is, Brane World cosmology) in the next chapter.
Let's stick with inflation for now. Andrei Linde seems to be very connected to the idea of chaotic Inflation and a bubbled multiverse.
In 29 october 1981, an article appeared called :
A new inflationary universe scenario: A possible solution of the horizon, flatness, homogeneity, isotropy
and primordial monopole problems.
True, later articles, as of 1983, referred explicitly to chaotic inflation. and it seems that most people refer to those articles.
More players than only Linde are active in chaotic inflation, especially from 1983 up to 1990 (or so).
Here are a few words on Linde's initial interpretation:
Chaotic Inflation (Linde):
After a "quantum fluctuation", a scalar field exists, with a certain initial potential ϕ energy.
You can indeed make educated guesses about that initial value, expressed in Planck Energy units, but Linde primarily
keeps his theory generic.
The value of the potential energy, behaves like a harmonic oscillator. Depending on the initial potential ϕ,
Linde shows that the value of the potential can "roll-down" rather slowly, or possibly"roll-down" rather quickly.
This is actually the "chaotic" in the name of his theory, since using various forms of equations for the initial potential ϕ,
(like polynomials, or others) does not really affect the main theme of his theory. Inflation will inevitably follow.
Here, the term "inflation" simply means "exponential expansion", like as you can write the expansion as an "e function".
In effect, Linde wrote down a relatively simple second order differential equation for the potential ϕ,
where as a term the Hubble parameter (H=a'/a) is present too (here, a' means velocity, and a is distance.)
Amazingly, it simply follows that:
H=a'/a=mϕ/√6 with as a solution a=eHt. (equation 6)
True, this is the most simple form, and more involved ones exists too.
Whatever you say, the startling thing is that, using almost highschool physics, leads to an exponential expansion,
and further he shows that the theory is quite immune to the form of the potential ϕ.
Next, Linde argues that if we take a good guess of the initial energy, then in about 10-30 second,
the Universe inflates with an order of magnitude of 10100 (or so), meaning that the Universe was already
way way larger than what we today say is "the size of the observable Universe".
It indeed would explain why the Universe 'looks' flat, since, even if it was curved on a large scale, we would never
notice that in our small patch of the Universe.
At a certain "moment" ϕ is very small, and starts to oscillate around a "minimum". This is a particle
creation phase, where particles "snows" from the Vacuum.
Alright, now we understand what the "chaotic" means! This actually is Linde's main theme.
But next, he makes Inflation "eternal"....
Bubbled Multiverse, and Eternal Inflation (e.g.: Linde, Guth, Vilekin and others) :
During the inflationary period, small quantum fluctuations in ϕ were actually very likely, and when, nearing the ending
of inflation, ϕ got smaller, and those quantum fluctuations were the cause of smaller "density perbutations" which
many folks see as the cause for later galaxy formation.
This idea holds for virtually any inflational theory.
Chaotic inflation, at least according to Linde, implies a self-reproducing Universe. The reason for this
are "large" quantum fluctuations during inflation, which increased the value of the energy density in ϕ, leading
to larger perturbations, and substantial "faster" inflation of such region.
Some interesting scenario's are possible:
Some authors (but a minority) see here the cause for "topological defects" or "domain walls", which ultimately
will seperate those pre-universes. This is not a mainstream view anymore, but I like to mention it anyway.
Linde argues that those subregions expands faster than the original domain, whereas in those subregions, the same
type of "large" quantum fluctuations may occur, which again leads to expanding subregions.
This ultimately leads to a "bubbled" Multiverse.
Some authors even do not rule out that in fact we have "eternal inflation", since in the scenario above, it's not
simple to say that there have to be a grandfather inflationary period perse.
But even in the scenario of a "true bootstrap", the "bubbled" Multiverse is a theoretically defendable proposition.
Although also matematical conjectures exists, to illuminate the above (although they are likely not "perfect"),
do not forget, that in an inflationary epoch, according to GUT theories, gravity and QM are very close.
Thus, the assumption of larger "quantum fluctuations" is quite reasonable.
Are they Testable theories?:
Recently, "gravitational waves" were detected. It was a very large event, and you can't have missed it.
It was on the news everywhere.
It's quite likely (or better: quite possible) that "ripples" in SpaceTime are going to be detected,
which, after analysis and interpretation, might be an indicator of an endphase of inflation.
When the LHC is fully operational again, and those folks at Cern are able to let protons collide with 14 TeV (or so),
then again these will be experiments with a higher energy, and smaller crossection, and again it represents a peek
into conditions of an earlier Universe (than we had before).
As an end remark, I must say that not all Cosmologists/Physicists, see the Inflationary scenario
as one that covers the whole package.
5. The Universe as an emulation, or "physical reality=virtual reality".
The Universe as an emulation, or virtual reality?
This sort of hypotheses are certainly not my favourites. It's sounds very weird, to view our Universe
similar to a "computer emulation", or as some strange form of "virtual reality".
Also, there are almost no physicists which give credit to any of these sort of ideas.
Still, it is an "option". Indeed, there exists some motivation for these lines of thought.
SpaceTime Quanta as bits
For example, Quantum Gravity theories propose SpaceTime quanta. This can be thought as dicrete units, which
form loops, or spin networks. Either way: they seem to be fundamental blocks, which seem to operate
on a scale of the length of Planck.
It is indeed tempting to view such a quantum as the most fundamental piece of information, like a "bit".
A bit in itself is no "information", but strings, or volumes, or surfaces (or whatever "construct") is information.
To project constructs of SpaceTime quanta, as something that can be compared to memory units, is fully speculative.
However, there exists a low number of 'believers', or also, scientists with a sufficiently open mind, that they
are willing to consider such ideas.
However, there is nothing very concrete from physics to offer here.
From information sciences, possibly "yes". There is a hypothesis of a "calculable Universe", which
essentially says that the physical reality can be simulated by information processing.
-But then it is probably not like a very sophisticated 'weather model', who's prediction seems to be right the next day.
-It then has to be deeper than the example above. It has to be something like 'the output of the calculable Universe
is physical reality'. The latter term (physical reality), probably must be understood to be "virtual reality".
Determinism:
It is certainly not so, that hypotheses like the "calculable Universe", float on determinism.
There seems to room for stochastic processes as well, in these theories.
However, full "determinism" in our Universe would be strange indeed, but then it might also form a case
pro "emulated reality" or "computed reality".
In QM, we have for example the famous EPR paradox. One possible solution is the assumption of "hidden variables",
which are undetected (as of yet) parameters, which can account for events we cannot understand so well,
like entanglement.
The debate is not settled yet, I believe. If ultimately it is found that "determinism" on a deep level is simply
a feature of our Universe, it might be a "pro" for some sort of "calculated Universe" model.
Quantum Computing (QC):
Something which is a remarkable mix of physics, engineering, and information sciences, is Quantum Computing.
It's something completely different from the "traditional" way of computing.
Indeed, remarks and notes have appeared related to "The Universe as a Quantum Computer".
Each time, solid pointers are not available, but the slogans are intruiging indeed.
It's fair to say that QC is still in it's infancy. As time goes on, we simply need to evaluate new
results and articles emerging from this field.
Other considerations:
Physics and information sciences, cannot be fully covering for such hypotheses as presented in this section, I think.
It seems to me that psychology, and philosophy must come into play too..., somewhere.
I don't know "where". But if "physical reality=virtual reality", then this also must be related to how we percieve the World,
and it thus seems evident that such sciences have something to say too.
What is the connection with Parallel Universes?:
If such supercomputer would exist, it surely must be able to run a lot of models (realities) in parallel.
That's the connection.
However, I feel that the statement above, contradicts the hypotheses as touched upon above.
Block Universe:
As a last subject for this section, I think the following qualifies too, to be mentioned.
An interesting idea is that of the "Block Universe". In essence, it seems to say that all events, in the past
the "now", and the future, is already fully encoded in the "Block Universe".
In effect: All of the space, and all time of the Universe, are there in the block.
It has primarily a certain (small) supporting base in community of philosophers.
However, some physicists do not reject this idea too, since it also provides a certain solution
to unsolved problems, like the "strange case of Quantum probabilities".
But you might argue contrary: Quantum probabilities disproves the "Block Universe", unless it also
provides for "branches" (or "splits" or "forks").
It's difficult to see a direct relation of the Block Universe" to "Parallel Universes".
Or, in how much this also connects to "determinism", or "hidden variables".
I only mention the idea, since you might argue that such "Block Universe", is the final computation
(everything is already completely "worked out"), by this Universe, like a Computed model.
In this sense, it fits into this section too, since it resembles a computed reality.
6. Brane - World Cosmology.
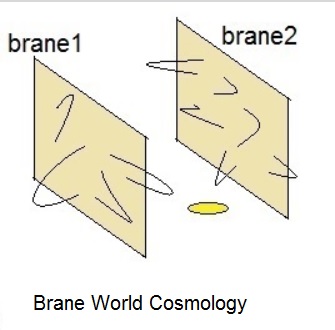
Fig. 2: A "Jip-Janneke" image, showing two manifolds (Universes) called "branes".
Gradually, during the development of String / M-Theory, hypotheses emerged, stating that isolated
branes (manifolds in "superspace") might represent full Universes.
This is completely based on theoretical considerations, but indeed also with some "speculative sauce".
As such, open strings (say the "normal" elementary particles or fermions), are bound to such manifolds.
In the figure above (rather exaggerated, indeed), you can see such strings (with their endpoints) bound on their "world".
Sometimes these hypothetical worlds are referred to as "Coulomb" worlds, since the ElectroMagnetic interaction
is one of the primary forces between open strings.
In principle, more than one such manifold could exist, thus resulting in multiple "branes".
The "stuff" between branes (if we may say so), is called "the Bulk".
Closed strings are not bound on manifolds. Here, one candidate boson could indeed be such "particle",
the "graviton", responsible for Gravity.
Since it is not bound, it may even escape into the Bulk.
Some folks see a clue for this, in the fact that gravity in small environments is such a very weak force,
while on a large scale, gravity is the paramount force.
This model is still "alive" among certain groups of theoretical physicists.
Numerous physicists work on String theory, and M theory, and Cosmological models based on both themes.
A specific model: The Randal & Sundrum model
First, a small remark. Although "Brane World" models are accepted as a possible solution for current problems (like the origin
of the Universe, Dark Matter, Dark Energy, and Unification of Quantum theories and Gravity), many physicists
are quite enthousiast for these theories. But at the same time, a lot are not.
The various models do not seem to be easily "testable". Ofcourse, science is Theory, in conjunction with Experiments.
However, there are some hypotheses which propose possible test scenario's, like the search to a "fifth" uncompactified dimension.
There are quite a few "Brane World" models actually.
Many modern ones are based on the Randal & Sundrum model, which is a (3+1) Brane in a 5 dimensional Bulk.
Please note that "the hyperspace" here is (4+1), meaning 4 spatial and one time dimension. The Brane then would be (3+1) manifold
in that (4+1) space. Here, one additional "extra" dimension is used, which is not compactified, and is only "accessible"
for gravity.
Further details on such a model can be found in a classical article (1999):
"An Alternative to Compactification (1999)", which can be found here.
Essentially, the authors describe a single 3+1-brane with positive tension, embedded in a (4+1) (fivedimensional) Bulk SpaceTime.
Using "gravity" as the vehicle to explore the scene, and using wavefunctions, they argue that a graviton in the Bulk neccesarily
will be in a confined bound state. Initially, they make no assumptions on the additional spatial dimension rc, so
it could be compactified. Using rather involved math and letting rc grow to infinity, they manage to keep
the "four-dimensional effective Planck scale", to go to a "well-defined value" as well.
This means that a consistent 4 dimensional theory of gravity could be derived from the used model.
Such a 5 dimensional model, using no compactification, is a remarkable deviation from M-Theory based models.
Secondly, the bound state of the graviton as described in this article, actually means that they are close to (or near "at") the Brane,
and do not travel "freely" around.
Note that, in simple words, we can now speak of "distances" along that fourth spatial dimension. If you would insist, you can still use
more compactified dimensions. However, the one that (probably) only gravity is aware of, is that fourth spatial dimension.
It could represent a "testable" scenario. Indeed, several searches have been performed. No luck yet, for those theories.
Note that the original Brane World scenario's, might imply "Parallel Universes".
The Randal & Sundrum model, is not really involved into "Parallel Universes", since there might only exist
one Brane and the Bulk. However, extensions hereto are possible, and the number articles in this field is quite large.
7. Proposed tests, using Quantum Mechanics and Quantum Computing.
I must say, and that's my personal view, that I do not see a relation of Parallel "Worlds",
and computing with a Quantum Computer. In other words: a Quantum Computer needs one Universe only, I believe.
But, it does not mean anything, that I have strong reservations.
Sure, many folks think differently, or have at least an open mind for such hypotheses.
Anyway, I like to spend a few words on various thoughts here.
However, I have extreme difficulties in finding "proper" models for "test scenario's".
A common "element" in Quantum Computing (QC), is the "qubit", which indeed is the basic "bit" in QC.
The basic expression for a standard Qubit is as follows:
|Ψ >= 1/√2 . ( |0> + |1> ) (equation 7)
Very often, the Qubit relates to the "spin" (which could be measured along some axis), and that "spin"
is an observable of some suitable particle (like the electron).
When measured, it is either found as "up" (|1>), or "down" (|0>). However, unmeasured, this observable
is believed to be in a superposition of |0> and |1>, exactly as shown in the equation above.
So, indeed a sum of both basis vectors at the same time.
There was, and still is, quite some debate if superposition is just a feature in the model, or that it
corresponds to a true physical feature, that is, that it really "exists".
Ofcourse, there is nothing special about "superpositions", and we can find it at many places in physics.
But as properties (observables) of (say) elementary particles, which seem to exist in a superpostion of
basis states, there were many, almost philosophical, related questions.
According to what we have seen in Chapter 3 (Poirier's theory of interfering "classical" universes (MIW)),
the classical and fixed values can be readily obtained in each "classical" Parallel Universes.
But those universes interact, and it sort of naturally follows, the "fuzziness" of Quantum Mechanics.
One might also consider Everett's Theory (Chapter 1, MWI), and see how it holds from the perspective of QC.
How can QC be used, to obtain evidence (or just a pointer) to the existence of Parallel Universes?
As already said above, I believe that it will not.
But many say that it can, or that it possibly can. Note the subtle difference here.
Indeed QC is very complex. Apart from that, as I see it, on the one hand, we have the (more or less)
true scientific QC implementations using qubits and "gates" (in the form of lasers or EM radiation etc..),
and we have rather strange implementations like for example those of the commercial D-Wave corporation.
So, am I saying that there are two "streams" in QC?
You can at least identfy three (sort of) streams in QC:
(1), In what I call "the first QC approach" of QC, and let's call that "the gate quantum computing".
(2). The "Quantum annealing" implementation by D-Wave (so I believe).
(3). Topological QC.
Some other lines of QC research takes place too, like those based on Majorana entities.
Some folks name (1) also "universal QC", since it seems that it can be applied to more algolrithms.
In order to say anything useful in the terrain of "Proposed tests, using Quantum Mechanics and Quantum Computing",
there is no other choice than to say some fundamentals those approaches first.
A few essentials of "Gate Quantum Computing" (general QC, or universal QC):
In general, QC is a bit "stocastic" in nature. For the algolritms I have "studied", like one
of the most simple ones as "Grover's algolrithm", it is really statistical.
So: as I see it, finding solutions using QC, is statistical in nature.
Let's first take a look at a classical case. Suppose you have a set of "N" values (or "N" records), and
you only want to search for one specific value, then on average "N/2" searches have to be performed,
assuming that we just have a "stack" or "heap" of values, and no "index" is present.
This is rather similar to a classical query on a database of N values.
Please understand that this specific value, is known beforehand ofcourse. For example, you have a search like:
"select * from 'stack' where id=5.
And suppose your heap of values counts 8 members, then on average, 4 searches need to be executed.
If the same would be applied in a QC, one might use the following approach:
Using the Algolrithm in a QC implementation, one tries to apply the "diffusion" operator in "iterations",
and steadily lowering the amplitude of non-solutions, so that the real solution starts to "stick out".
The algolritm is "statistical", meaning that after "m" iterations, there is a very good chance of finding
the correct answer. The larger "m" is, the better that chance on finding the solution will become.
Suppose one starts with a three qubit state in the form:
|Ψ>= 1/√8 |000> + 1/√8 |001> + 1/√8 |010> + 1/√8 |100> + 1/√8 |110> + 1/√8 |011> + 1/√8 |101> + 1/√8 |111> (equation 8)
You might wonder how such a superposition is establised.
An example from just 2 qubits might help. If they are really close, but not entangled, the composite system
is the tensor product from the individual states. It's actually also a postulate in QM, but the model works.
So, suppose we have:
|φ1> = a|0> + b|1>
|φ2> = c|0> + d|1>
Then the tensor product is:
|φ1> ⊗ |φ2> = a11|00> + a12|01> + a21|10> + a22|11>
A similar product can be done with three qubits.
You might view equation 8 in this way, that |Ψ> is expanded into 8 basis states, each with a probability of 1/8
to be found when a measurement on that system is made.
Now, let's return to the 3 qubit composite system again.
Now, choose a certain substate of these component states. Then that one will function as "the record" which must be found
by the quantum algolrithm. So, we could choose |010> or other of these 8 components.
In this sense, |Ψ> looks like our "database".
So, let's take for example |010>
(1). Marking the Solution:
Now, one Quantum feature of this quantum algolrithm, is to "inspect" all entries at the same time.
Note that this is not to be taken lightly. This is parallel processing.
It is possible, that the "solution" gets marked, for example by inverting it.
Just as in the classical case, there is nothing wrong that the solutions is known beforehand.
The same was true in the classical situation too.
Often, in QC as it is now, one goal is to compare the speed and efficiency of certain protocols,
using Quantum- and classical algolrithms.
Ofcourse, for some Quantum Algolrithms, there does not even exist a classical equivalent.
The term "Inspecting" does not mean "making a measurement". It might mean that we apply an operator (by some gate),
like implementing a "phase shift" or "inversion", or anything else suitable, on the components.
Ofcourse, just like the classical case (where id=4), the mode which we want to search for (|010>), is known.
(2). Applying the diffusion operator:
The algolrithm furher starts to "stick out" the amplitude of |010>, and tries to diminish the amplitudes
of the other modes.
In this particular case, the process works in iterations. The more you apply, the better the statistical
change to select |010>, because now it sticks out "more and more" from all the others.
In classical terms, it "looks" like a query to find the one good answer from N values.
In the classical case, the answer returned is 100% correct, but on average the system must query N/2 values.
In turns out, that in general, the QC algolrithm performs better, using more qubits, and (hoping)
that "m" (number of iterations), can be kept rather limited. But: it's statistical.
A garantee on a 100% correct answer cannot be given, unless m gets higher and higher.
In this example, the diffusion operater is logically symbolized by "logical gates", which are
are the Quantum equivalents of Boolean gates (in traditional computing).
The physical implementation of such "gate", depends also on how your "qubit looks".
The quantum gate could be a laser pulse, an ElectroMagnetic pulse etc..
I think that such description seems rather typical for QC, at least for the algolritms I have "touched upon".
However, I must say that I have only followed (theoretically studied), just a few algolritms.
In the upper case, entanglement of qubits did not played a role. But entanglement
between qubits is essential for certain other Quantum Computations.
However, no matter how important entanglement might be, the pure parallelism on a superposition
is a key concept of QC too. If you have a Gate "H", and apply it to input which is in a superposition,
then it is applied to all component vectors in that superposition simultaneously.
Now, here is my crux. Personally, I do not see any relation to Parallel Universes, for now, unless
the very idea of "quantum superposition" implies it (as theories of Pourier and Everett uses it).
But I must repeat: my opinion means "0", or "zippo", here, since well-know physicist
are really quite serious in relating QC with Parallel Worlds.
If you like an intro on "universal QC", you might like the following article:
An Introduction to Quantum Computing for Non-Physicists
A few essentials of the D-Wave "Quantum Annealing":
A few large and well-known companies or organizations have implemented D-Wave systems, like Google, NASA.
Rather interesting projects have been started, like further investigating AI using D-Wave systems.
D-Wave has, over a few years time, delivered systems using 128, 512, and over 1000 qubits. These are astounding
numbers for physicists working in the field of QC.
There were times that I seriously thought that D-Wave did NOT produced the "real thing".
The whole reason I bring up the D-Wave story at all, is that some important folks working at that place
on several occasions have stated that their systems, in operation, "are tapping into Many Universes...".
Wow..... Then we must also take a look at these methodologies.
There seems to be something "strange" about those D-Wave systems. First, so many qubits on a single chip
is indeed quite unheard of. Is the whole thing really a Quantum Computer?
I have to say that I also listen to the people who are really active in the field, and indeed many
were initially extremely skeptical, but slowly, many views have turned to the opinion that the systems
are indeed Quantum Computers, but only are using a very specific principle, suitable for very specific algolritms only.
The principle D-wave uses is called "Quantum annealing". One feature this methodology uses is Quantum Tunneling".
That is the principle that a "wavefunction" has a non-zero probability to penetrate a barrier, which
classically spoken would not be possible.
A famous example is a particle (or wave) in a Potential Well, for example in 2 dimensions (x- and y axes).
For example, the potential at the "vertical" barriers "x=0" and "x=1", is very high, or maybe even infinite.
Classically, the particle is confined between the two barriers. However, from a QM perspective, the particle/wave
has a certain probability to "tunnel through" such barrier.
I am not a D-Wave expert. But one sort of theme can be found, by studying their articles.
One of their tracks even has some similarities with database technologies.
Suppose you have a very large "fact table". This one has a certain number of columns, and probably an
enormous number of rows. To "track" relevant information from that 2 dimensional object, can be a huge task.
If you connect that table, with just one dimension of information (another table) you are interrested in,
(which might e.g. only list regions, or products, or total sales etc..), then you have have constructed
a 3 dimensional "cube" of n-tuples.
If you are interested in such model, in maxima and/or minima, the "tunneling protocol" might
enable you to find such information faster than compared to traditional analysis.
In Jip-Janneke language: the tunnels go through barriers to find such minima (of "cost functions") only.
This does not explain the used algolrithms ofcourse, but it might help in visualizing in
what D-Wave systems might do, when extreme points must be found in large bulks of data, like for example
strong pressure points on a complex geometrical object, in some force field or fluid field.
Now, at least we have a simple representation of QC, both using "Quantum Gate" computing, and "Quantum Annealing".
By the way, the following article is how Nasa is using, and think to use, D-Wave systems. It tells a lot on the principles:
A NASA Perspective on Quantum Computing: Opportunities and Challenges
Topological QC:
-(Ordinary) Hall effect:
Suppose you have a flat conductor, and an elecric current is flowing in that conductor. If you introduce a Magnetic field
perpendicular to the conductor, the electrons will be pushed to one side of that material
due to the well-known (classical) Lorentz force on the electrons.
The "classical electric current", was always supposed "to flow" in the opposite direction.
In the upper case, you might view that classical current as "quasi-particles" flowing into
the opposite direction as the electrons do.
-Quantized Hall effect:
If a sheet of very thin suitable material is cooled down, to near 0K, and a strong Magnetic field
is applied, the electrons in that material form particular structures, with particular densities
and the "Hall conductivity" takes on very precise quantized values.
At the time that this was discovered (around 1980), it was soon realized that this might represent
a new perspective on Quantum Physics, on many particle systems and fields.
In fact, ingredients as geometry and topology turned out to be essential for describing the
"Quantized Hall effect".
-Loops:
One remarkable sitution may appear, where electrons form partners, and such subsystems move in loops
in the plane perpendicular to the magnetic field. These loops are quantized too.
It is often said that they behave as "quasi-particles" (called anyons).
These loops form the basis for qubits and gates.
Much research is going on today. A further remarkable benefit is that such "loops" are almost
not at all effected by decoherence, which always plagues the (gate based) "universal QC".
The robustness follows directly from topology: if you have a coffeecup, and some pieces fall off, you still
have a coffeecup, unless the typical handle falls off too, which changes the topology fundamentally.
This makes Topological QC possibly the best candidate for QC.
If you would like a good overview on Topological QC, you might like:
A Short Introduction to Topological Quantum Computation.
Proposed test scenario's:
Still did not found any plausible or reasonable proposals for test scenario's using QC.
However, there exists many articles using Superposition, or Entanglment, for constructing testscenario's
applied at Everett's MWI, or Porier's MIW theories.
You can google on such terms and using the keyword "arxiv" as well, to view such scientific articles.
But, I am explicitly searching for a testscenario using QC (in some way..., whatever way...).
8. The "Many Minds" theory.

