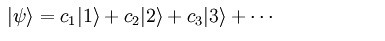A few notes on Entanglement, Decoherence, and other aspects of Quantum Mechanics (QM).

Contents:

1. A few words on "entanglement
2. A few words on "non-locality"
3. A few words on (classical) "Copenhagen interpretation"
4. A few words on "Decoherence"
5. A few words on Everett's "Many Worlds" Interpretation (MWI)
6. A few words on Porier's "Waveless" Classical Interpretation
7. A few words on de Broglie - Bohm "Pilot Wave" Interpretation (PWI)
8. A few words on Weak Measurements and TSVF

1. A few words on "entanglement":

Probably the discussion in this section is a bit too "Copenhagen-style" oriented, but that is how entanglement
usually is introduced, in most literature.

Erwin Schrödinger came up with the expression “entanglement”, and called it “the" characteristic trait of quantum mechanics.

Many of us probably have heard of it, but often it is felt as a rather "strange" effect.

Indeed, what is it ? Let's consider a two "particles" system. In a special case, their common state can be in such a way,
that we may only describe it effectively as being two parts of the same entity.
Like the word "entanglement" already suggests, it's a sort of "correlation". In better words:
you need both particles in order to fully 'describe' the state of the system.

Fig 1.

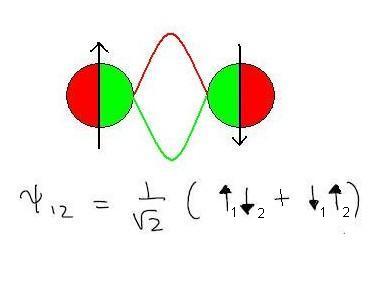
The Ψ(r,t) function of a single particle in QM, describes the system as a distribution in space (r) and time (t).
When you would consider a two particle system, the state of the two-particle system would described by the wave function Ψ(r1,r2,t).

If we would leave out time for a moment, and if the particle one is in ΨA(r) state and particle two is in ΨB(r) state,
then the total state can be written as the product Ψ(r1,r2)=ΨA(r1) . ΨB(r2)

But the "expression" as shown in figure 1, is quite different. Here it is not possible to seperate the entangled state
into product states.

In figure 1, you see up and down arrows. This is so, because in this example, we are looking at a special property
that a particle might have, which is called 'spin", which can be thought of as some sort of "angular momentum".
Note that many articles use entangled photons, where the "polarization" is used in a similar sense.

Take a look at this expression again:

Ψa,b=1 / √ 2 ( |↑ ↓> + |↓ ↑> )

Now please notice this: It's a quantum superposition of two states, namely ↑ ↓ and ↓ ↑ ,
which we might call "state 1" and "state 2". In such a state, as for example | ↑ ↓ >
we see particle A as ↑ and particle B as ↓

In state 1, Particle A has spin along +z and particle B has spin along -z.

In state 2, Particle A has spin along -z and particle B has spin along +z.

(here in this example, we look with respect to the z direction; but any other direction could have been choosen)

Now suppose the particles are moving in opposite directions.

Alice has placed a detector where particle A will fly by, and Bob did the same at where particle B goes to.
Alice now measures the spin along the z-axis. She can obtain one of two possible outcomes: +z or -z.

Suppose she gets +z. According to what we know of the collapse of the wave function, the quantum state of the system
will collapse into state 1.
Thus Bob then will measure -z. Similarly, if Alice measures -z, Bob for sure will get +z.
No matter what the distance between Alice and Bob is.

Isn't that amazing? If Alice gets +z, Bob gets -z, and the other way around. How do both particles know that?
I mean: the entangled system is in a superposition of |↑ ↓> and |↓ ↑>.
Especially when the distance between particle A and particle B is large, it's quite puzzling.
However, most physicist don't believe that a superluminal (faster than light) signalling operation is at work here.
But what is it then?

First I have to admit that in the example above, I oversimplified matters. In experiments, in fact statistical results
are obtained, using many entangled particle systems. Due to various reasons, not only the spin along z is measured, but also along
the x (or y) direction. Finally, the results are tested agains te socalled "Bell" (or derived) inequalities.
But.. currently, all results seem to sustain the conclusion of the example presented above.

Many "suggestions" have been forwarden, like "hidden variables" (which we don't know of yet), which works in such way
so that from the start of entanglement, a sort of hidden "contract" can explain the oserved effects.
But many other "explanations" go around too, like Multiple Universes (MWI), or some still do believe that a "spooky action"
that exceeds the speed of light is at work, or that our interpretation of space-time isn't correct etc.. etc..
However, many physicists say that the observed results happen with "probabilities" and this type of correlation
does not automatically imply communication.
Indeed, most physicist accept that non-locality effects of this sort, is simply "non-signalling".

Note that a key point is, that the entangled system is in a superpostion (thus both simultaneously) of two states ↑ ↓ and ↓ ↑.
According to the Copenhagen interpretation, when a measurement is done, the system "collapses" into one state.
A puzzling element still remains, that a superpostion of states exists, no matter how far the particles are apart. But when
for example particle A is measured as ↑ , then B will be ↓.
So, what is the meaning of the original superposition?

2. A few words on "non-locality":

Now, intuitively, if particle a and particle b are really close together, we might not be too disturbed, if on the left,
we measure "up", and on the right we measure "down" (or vice versa), although it doesn't feel right acording to the superposition
principle of substates, as expressed in QM.

But now, suppose that the detectors "left" and "right" are really quite far apart, and if we then still observe the same
results, it might get more puzzling.

Suppose partice a is found to be "up". Now suppose particle "a" has a nifty "means" to inform "b", that it was measured as "up", and thus
"b" now knows that it has to be "down". Now suppose that really such a fantastic mechanism would exist.
But there is a problem if the distance between "a" and "b" is so great, that "a" would have to use a mechanism that exceeds the
speed of light.
Indeed, certain experiments suggests that the correlation still remains, even if there is no way that "a" can inform "b", or "b"
can inform "a", how it was measured, unless a superluminous signalling mechanism would be at work.
Clearly, that is not generally acceptable, since it conflicts with Special Relativity Theory of Einstein.
Also, this is what Einstein called "the spooky action at a distance".

You know, there are many "interpretations" out there, to explain the effect.
When you would believe in "Local reality", you would say the state of an observable
would be clearly defined. Now, you could measure some observable and obtain a certain result.
It's quite accepted, that when you measure some observable, in many cases you would interact with that system,
and thus you would have exterted some influence on that system.
It's "pretty close" to what the idea of "local realism" actually is, but not entirely.
Local realism is somewhat opposed to what QM seems to "look like": QM is probabilistic in nature.
If you would favour the idea of local realism, you probably would not like QM too much, and you might argue that
QM can't be a full and complete theory.

The essential meaning of Local realism then would be, that a system truly has some defined state, and is not "fuzzy" at all.
Even if it would just "appear" to be probabilistic (fuzzy), then below the surface, something like "hidden variables"
are at work, (which we don't know about, yet) which would make it "exact".

The "hidden variables" would then also be the mechanism to explain the seemingly non-local effect, as we have seen at those
two particles, seperated over a long distance.

However, most physicists accept that "non-locality" is a fundamental aspect of Nature.
Some scientists have come up with some other very interesting arguments. In effect they say:
We are used to the fact that space and time are our defining "metrics" to valuate experimental results.
But (as they say), quantum non-locality shows us that there has to be more, something that we are just not sure about yet.

There are some ideas though, on the "new" structure of space and time, to explain nonlocality.
One idea is the concept of "prespace". Partly based on original ideas of Bohm, Hiley (and others) formulated the concept
of "prespace", which essentially says that the "usual" space-time manifold emerges from a more fundamental level of physical space.
Using a "Quantum Potential" and a new revised idea of "time", they formulated a framework which might explain nonlocality.

Another great way to theoretically analyze entanglement, is the EPR wormhole.
Some (theoretical) physicists, are working on models that associate the smallest
space-time building blocks, with socalled ER=EPR Plank-scale "wormholes". In many cases, they focus especially
on the Quantum Mechanical effect of "entanglement", and believe it or not, some articles make sense how such planck scale
wormholes connect entangled particles. However, many physicists are sceptical, and like much more "body" on those models.

3. A few words on the (classical) "Copenhagen interpretation"

The measurement of an "observable" of a system like a particle, can be described in several ways.
One method which "seems" to be quite natural in QM, is to to describe the system as a superposition of "eigenfunctions",
just like you can describe a vector in n-space as being composed of n orthogonal eigenvectors.
(Note: Below is a very simple example of a socalled a "bra" "ket", that is,"|>" equation.)

Fig 2.


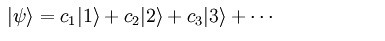
In this way, it's also described, what the "probabilities" of the possible values of the observable could be.
These probabilities are namely related to the coefficients of the above equation.

So, let's suppose that some sort of "measurering apparatus" finds value "c3", then at least one important question arises.
Why did the system collapsed into the state c3|3>, and what happened to all the other eingenstates?

This is an example of the socalled "collapse of the wavefunction". If an actual measurements is done,
out of many possible results, just one is "selected" in "some way"
An observable, initially in a superposition of different eigenstates, appears to reduce to a single value
of the states, after interaction with an observer (that is: if it's being measured).

It has puzzled many people for years, and different interpretations have emerged.
Although "Quantum decoherence" (more on that later) is quite accepted by most folks nowadays,
other interpretations exist as well.

The so-called "Copenhagen" interpretation, accepts the wavefunction (or state vector) as a workable solution,
and the collapse that happens at a measurement, is a way to describe why a particular value is selected.
As a simple example, they would say that a system can for example be described as Ψ = a|1> + b|2>,
and we have probability |a| to find the observable to be in state |1>.

So, it says that a quantum system, before measurement, doesn't exist in one state or another,
but in all of its possible states at once.

The "Copenhagen" interpretation is most often "associated" with the principle of the "collapse of the wave function",
when a measuerment is done. But it does not strictly mean that all who favour this description,
also believe in the physical reality.

Bohr seemed to have gone one step further (in a later phase), by essentially saying that the wavefunction
is not equal to a "true" pictorial description of reality, but instead is (just) a symbolic representation.

With a litle "bending and twisting", you might call this view and methodology, something like the "early"
cornerstone of QM. The theory is succesfully applied at many physical systems.
For example at the Hydrogen atom, any eigenstate of the electron in the hydrogen atom is described fully
by a number of quantum numbers. Also, the actual state of the electron may be any superposition of eigen states.

However, important insights which differ greatly from the "Copenhagen" interpretation, surfaced more or less at
the same time. An important one is the "deterministic" and realistic Hidden variables Quantum framework,
and ofcourse the Pilot Wave interpretation developed by de Broglie around 1927 and further refined
by Bohm around 1952.

In the Copenhagen interpretation, the wavefunction is a superposition of eigenstates. In slightly different words:
It says that a quantum system doesn't exist in one state or another, but in all of its possible states at once.
A very simple example is this: Ψ = a|1> + b|2>
It's only when we observe its state, that a quantum system is forced to choose one "probability", and collapse
into a certain eigenstate (which produces a certain value for an observable)
So, When we observe an object, the superposition collapses and the system is forced into one of the states
of its wave function.

In figure 3, you see a few other examples of "superposition", and ways to denote the wavefunction:

Fig 3.


Many people have disliked the postulate of a wavefunction that collapses, without a associated physical reality, as was
implied by the Copenhagen Interpretation.

One philosophical question is this: How and why does the unique world of our experience, at measurement, then emerge
from the multiplicities of all alternatives available in the superposed quantum world?
Also, as said before, the Copenhagen interpretation states that a quantum system, before measurement,
doesn't exist in one state or another, but in all of its possible states at once.

One classical "thought experiment" tries to illustrate the shortcomings of the Copenhagen interpretation.
It's the famous "Schrodinger Cat" thought experiment.

Schrodingers Cat:

When taken literaly, and to the extreme, a nice (and famous) paradox can be constructed. Suppose a cat is trapped
inside a completely sealed box. Inside the box, a radioactive source is present with a certain QM probability to decay.
If that happens, some mechanisme activates, and it releases a deadly poison, that will kill the cat immediately.
Now consider an external observer, who does not know the state of the cat.
Under the Copenhagen description, the observer whould describe the cat as: |state of cat> = a|alive> + b|dead>.
Only when a "measurement" is done, that is, the observer opens the trap and checks the state of the cat, that state
would collapse to either "dead" or "alive". This is ofcourse somewhat absurd.

Now, this "macroscopic" example, is really not quite comparable to the microscopic world where QM seems to dominate.
The point seems to be, that the paradox nicely illustrates how hard it is to deal with the description
of a superposition of states, and the collapse of the wavefunction.

Among other interpretations, three other important interpretations emerged.

• The "Many Worlds Interpretation (MWI)" dates from 1957.
  This theory, although it's quite consistent, never had too many supporters (at that time).
  By a Quantum event, where we formerly would say in the Copenhagen language, that the superposition collapes into
  an eigenstate with a certain probability, in MWI it is proposed that the World forkes into different Worlds
  in accordance to the number of superimposed subwaves which all could have been observed.
  Hence, Many Worlds come into existence, and all different parallel Worlds will evolve independently.
  
• The other one, "Decoherence" stems from around 1980-1990 (or so), and received quite much acceptance in the physics community.
  It mainly provides for an explanation of the strange "collapse" of the statevector.
  Roughly, it says that due to the interaction of the Quantum System with the environment (or measuring device)
  only selected components of the wavefunction are decoupled from a coherent system, and are "leaked" out
  into the environment.Ultimately, we will measure only one component of such selection.
• The "Pilot Wave Interpretation (PWI)" was developed by de Broglie in 1927, and work was continued by Bohm in 1952.
  It's an almost classical interpretation. A real particle, is guided by a distributed "guiding" wave.
  If you see this theory in scientific articles, then you would appreciate the fact that quite a few paradoxes are "solved"
  (like the wave-particle paradox), as many see it.

The first two above still use the "state vector" or "wave function" as proposed Schrodinger, Bohr and others.
but the interaction with the environment, and measurement process is quite different from that of the collapse
used in the Copenhagen interpretation.

The "Pilot Wave Interpretation" uses real localized objects, with a complex Pilot wave, which shifts all "wavy" stuff
to the Pilot wave itself.

A very recent interpretation eliminates the wave function all together. Around 2012, an interesting model was established
by Bill Poirier. Here the "wavy" stuff and associated probabilities, is an illusion due to the fact that classical
parallel universes exist, where in each of them, the Quantum System has clear defined values.
It simply just depend in which universe the observer interacts with the Quantum System.

Below you will find sections which briefly will touch those different interpretations.

4. A few words on "Decoherence":

This rather new interpretation, has it's origins in 1980s and 1990s. In a sense, this theory "de-mystifies" certain
formerly unsolved mysteries, for example, why and how a quantum system interacts with the "environment", and
the "measuring device".
Also, the Copenhagen phrase "Collapse of the wavfunction" is replaced by quite a solid theoretical framework.

Many physicists have embraced the theory, and it seems that only a minority of sceptics remain.
Especially technical and experimental oriented physicst, for example working on the field Quantum Computing,
see the theory as one of their primary working tools.
(For example, sometimes they want to preserve a qubit or nqubit for some time, before it de-coheres).

However, in general, we all must be carefull in associating "truth" to any theory at all. It's just characteristic
of science, that theories ever evolve, and once in a while, even get completely replaced by better ones.
But the "decoherence" framework, is might well be, the best interpretation of QM we have right now.

Decoherence is important in the area of "the measurement problem", possibly also to "the flow of time", and
above all it's very appealing for most physicists because it seems to solve the question on how the "classical world"
emerges from quantum mechanics.

Key to the "Decoherence" interpretation, is that it was realized that the "environment" and the quantum system (like a particle)
are really tied into a temporary "entangled" system, for a certain duration.
Ofcourse, it was already long known that a measurement will influence any system, but this time, a whole framework
emerged from "the deep intertwinement" of the quantum system and the environment.

In a nutshell, the central idea of the theory goes (more or less) like this:

As usual, initially, an undisturbed quantum system, is a superposition of coherent states.
When the quantum system and the environment (the environment as a whole, or a measuring device) starts
to interact, the coherent states will "decohere" into socalled "pointerstates" which are really
determined by the environment. It means the loss of coherence or ordering of the phase angles between the components
of the quantum superposition. Effectively, the Copenhagen "phrase" "collapse of the state vector",
this time has a real physical basis or "explanation".
After the system has decohered, these "pointerstates" corresponds to the eigenstates of the observables.
In other words, only selected components of the wavefunction are decoupled from a coherent system, and are "leaked" out
into the environment.
This selection of pointerstates is also called "einselection" in various articles describing decoherence.

Again rephrased in slightly other words: the wavefuctions of the environment and the quantum system, will interact
in such a way, that the coherent superposition of the quantum system will de-cohere and "ein-selected" states
remain, which resembles a classical system again.
This too is quite important: before the decoherence phase, the system is truly a Quantum sytem, that is, a superposition.
Then, after the "perturbation", or de-coherence phase, the system behaves much like a classical system.
So, for the first time, a clear boundary has emerged between a pure Quantum state, and what is believed to be "classical".

Note that the theory provides for a better explanation for what happens at a measurement, or interaction,
with the environment, compared to the Copenhagen interpretation.

For example, do you notice that "Quantum decoherence" only gives the appearance
of wave function collapse?

In the interpretation using the principle of "decoherence", is not possible to separate an object being measured,
from the apparatus performing the measurement. Or, to seperate the object from the "environment".
In this interpretation, in any interaction between the system and the environment, decoherence takes place,
and not just when you use some measurement device.
Generally speaking, the environment and the particle are bound, or entangled, in such a way, that only a subset
of superimposed waves (the "pointerstates) is "selected".
After the de-coherence phase, the actual value of an observable is selected from the pointerstates.

This new interpretation has quite some philosophical impact as well. The theory further describes how the environment
sort of "monitors" the de-cohered systems, and it affects our human perception as well.
There is a sort of redundancy of the pointer states in the environment, simply because there is "a lot" of environment
out there. So to speak, the environment "bans" arbitrary quantum superpositions.
Once a system has decohered, and only pointerstates remain (determined by the environment), and we as observers
come on the second place. The environment "observes" the system, and determines what "we get to see" from the system.
Ofcourse, any apparatus is part of the environment too, so it makes sense.

What might be nice to notice, is that the "decoherence" theory implies that the quantum wavefunction is a physical reality
rather than a mere abstraction, or postulate, as in many other interpretations.

Non-locality and Decoherence:

Nonlocality is hardly seen at macroscopic level because of "hard" decoherence, caused by so many interactions
with the environment.
But what happens with two entangled microscopic particles, flying away in different directions, and keeping their "correlation"?
In section 2, we touched on that subject. First of all, non-locality still seems to be a fundamental feature of QM.
Non-locality is ofcourse more than just the example of the two entangled particles of section 2.
However, it's still a "strong" example of nonlocality, that is, the absence of a local agent (see section 2).

But decoherence is a "powerfull mechanism" to destroy quantum features, so what about "non-locality"?
It's not easy to answer this one. Much experimental work, and theoretical studies have been done, and it's
probably fair to say that a very conclusive answer is not reached yet.
At first sight, decoherence might look like a local mechanism (like a quantum system that interacts with the local environment),
but probably it is not, according to some studies.

However, other studies have shown that non-locality seems to be very "robust".

5. A few words on "Many Worlds" and "Many Minds" Interpretations:

QM is absolutely astonishing by itself, but when we go to the Many Worlds interpretation, the excitement-level "shifts gear"...

We know what the Copenhagen Interpretation globally means:

An a quantum system, initially in a superposition of possibly many states, appears to reduce to a single value
of the states, after interaction with an observer (that is: if it's being measured).

So, at the moment of measurement, the wave function describing the superposition of states,
appears to collapse into just one member of the superposition.

In figure 3 above, we already have seen a few simple forms of a superposition of states.

Take a look at figure 3, example1, again. Now, suppose, that in a subtle manner, we rephrase the former statements like so:

A superposition expresses all possible "alternatives" for finding the value of a certain observable.

Expressed in this way it get's somewhat more plausible, that all the other "alternatives" may have realized
in other "branched off" Universes.

Above is not exactly the way that Everett originally formulated it.
His theory goes "more or less" like described below. But whatever your opinion will be of the MWI, it really does resolve some paradoxes in QM,
like the strange "collapse of the wave function", and even provides a solution for the non-locality puzzle (section 2).
And..., some core aspects of the "Decoherence interpretation" (section 4), looks remarkably to the central statement of MWI.

In MWI, there is no "collapse of the state vector". Suppose you do a measurement on a quantum system.
Before you actually perform the experiment, the system resides in superposition, meaning in all possible states at once.
This is what we already new from an undisturbed quantum system.

Now you perform the measurement, and you find a certain value. In MWI, different versions of you will have found
all the other possible values of the observable. It is as if the current Universe has "branched", or "forked", into
multiple Universes where each version of you, is happy with it's own private value.

I hear you think.. "Will then the Universe be rebuild N times, at each ocurrence of such an event and so on and so on..?
No. The trick is in the superposition. The alternatives "are already there", so to speak.

Everett realized, that the observer (with measurement device), and the system, forms a deep intertwined system.
Each "wave" of the superposition will "sort of interact" with the observer-measurement device.
From a mathematical perspective, this pair will split off, and further evolve independently from all the other possible "pairs" of
the {wave elements of superposition - observer}.
Hence, a number of independtly forked Universes will occur.

Do you see the resemblence with the Decoherence theory? Only this time, no environment driven pointerstates are created,
but contrary all "relative states" will "start an existence of their own".

But, intuitively, you might say, as I do, "this can't be the way the Universe operates..."
Indeed, many physicists nowadays say that the MWI theory does not provide an adequate framework on how a
many-branched tree of Worlds comes into existence.

6. Parallel Universes and the "Wavefunction-less" model of Poirier.

Around 2012, an interesting model was established by Bill Poirier.

He sort of "scrapped" the "wave function" or "state vector" completely, and assumed parallel (thus multiple), classical-like universes,
where observables of entities (like particles) have well-defined classical values.
His theory treats the collection of universes as an ensemble, and this only creates the "illusion" that
a particle might be non-localized in position or momentum (or any other observable).
So, while a particle might only appear to have a stochatic character (probability) in some observable, it's actually only
due to some "indifference" in which universe the oberver resides.

This supposedly explains why QM might "just look" as intrinsical stochastic, but it's actually the interactions between those universa,
that sits behind the observed effects.

Poiriers mathematical framework, is often called a "trajectory-based" Theory of (Relativistic) "Quantum" Particles.

Instead of his original article, I personally find the following 'follow up' article of much more interest, since the authors
provide for explanations for (for example) the double split experiment, quantum tunneling and that sort of typical QM manifestations.
If you like to see that article, you might use this link.

7. A few words on de Broglie - Bohm "Pilot Wave" Interpretation

This rather peculiar view was first developed by de Broglie in the late twenties of the former century. Then, later on
around 1952, it was picked up again by Bohm who made quite some further progress on this theory.

Strangely, it became never so popular during the 20th century, compared to the Copenhagen interpretation, and later, decoherence.
However, I seem to notice some gaining in interest (by simply scouting articles), since 2000 or so.

Note that it was de Broglie who first attained a wave-length to a typical corpusculair entity like an electron.

While the Copenhagen interpretation, and it's "collapse", is quite hard to link to reality, the "Pilot Wave" Interpretation
re-introduces again some classical features again. Not literally, but essential the theory states that we have a real particle,
with an accompanying pilot wave, which can be regarded as a "velocity field" guiding the particle.
Bohm further defined an "oncology" or framework on the essential ideas, which made the wave to be compatible with
Schrodingers equation, and thus further is deterministic (in the sense of given initial conditions, the further evolution
can be calculated).

If you are interested in a mathematical framework of this theory, I advise to Google on "Pilot wave arxiv",
which should return many scientific articles.

Amazingly, since the early 2000s, it was discovered that small oildrops in a bath of oil, show striking
similarites with the core idea of the Pilot wave guidance.
Maybe you like to see the following YouTube clip:

The pilot-wave dynamics of walking droplets

If you have viewed this clip, then you saw a great pictorial "emulation" of the key concept of this theory.

8. A few words about Weak Measurements and the Two State Vector Formalism:

If there is something else quite stunning in recent findings in QM, it must be the implications of the socalled
"Weak Measurements" and the Two State Vector Formalism.

Ofcourse, again different interpretations are possible, but one implication seems to be that
if you measure an observable without (hardly) disturbing it (and then ofcourse you need to repeat that many times
to get any significant result to standout above the noise), then it seems that;

Pre-selected results (in the past), and post-selected results (in the future), may have impact
on what you measure presently.

Take a closer look at those last few words: it's not the normal causality that we are used to.

These new formalisms use a time-symmetric model, instead of the usual "standard" approach used in QM.

If you want to read more, take a look at:

a few notes on "weak measurements" and QM paradoxes.