A few simple notes on the Higgs field and boson.
Version : 0.8
Date : 10/03/2012
By : Albert van der Sel
For who : For anyone who likes a very simple explanation of Higgs.
Contents:
1. Introduction
2. A few highlights in the standard model, and elementary particles
3. Why Higgs? A few notes on symmetry breaking, and the Higgs field
1. Introduction:
The Higgs field is believed to be an all permeating field in space, responsible for "attaching" mass to elementary
particles like the electron and quark.
You probably know, that mass is that perculiar property of an object to resist changes in motion. This rather Newtonian
interpretation, equates to "inertia": the unwillingness to accelerate.
The more "massive" a particle is, the more energy it will cost to set it into motion.
As an analogy: It is "as if" the vacuum (the space all around us, everywhere) acts as if it's really an ocean.
Suppose you are an elementary particle. Then all of the water is the field, and as you travel through the water
you will experience the "drag", that is, you interact with Higgs bosons.
The more "drag" exists, the more massive the particle is.
Or, in other words: the coupling to the Higgs boson is proportional to the mass.
Fig 1: a simple analogy of the Higgs field and bosons.
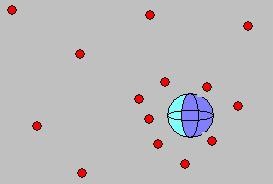
In the figure above: the gray space surrounding the particle is the "Higgs field", while the exponents of Higgs,
are the Higgs bosons (red dots) interacting with the partice, through which the partice aquires "mass".
Often, the existence of the Higgs scalar field is discussed, in studies of the "symmetry breaking(s)"
that occurred moments after the Big Bang. At those moments, the state of the Universe
is regarded to changed into a "new state", where elementary particles, and various force carriers, emerged.
The Higgs field then, came into existence when the spontaneous breaking of electroweak symmetry occurred.
When you look at it the "reverse" way, unification of the electromagnetic and weak nuclear force
into a single electroweak force, is believed to happen, when the energy (or Temperature) is high enough.
This is one important research area of high-energy physics, using large particle accelerators.
Note: Many physicists don't think that "one (type of) Higgs" found, will solve the "problem".
Since all forces should probably unite in a "supersymmetric" model, maybe several "Higgs" are needed.
More on this later on.
As an interesting side-step, even much closer to home (in smaller Labs), at least one of the paradigms
of the Higgs mechanism might already have been observed !
Undoubtly, you have heard of "superconducting" materials, usually cooled to very low temperatures.
In such experiments, the Magnetic field has been completely removed from the centre regions of this material.
This "Meissner" effect has indeed several explanations. One explanation is, that the usual electromagnetic field
(with the photon as its force carrier), cannot penetrate the material as usual.
To explain it, the theory used, is in effect an "abelian" example for the Higgs mechanism.
If the theory passes, it does not mean the Higgs boson is proved, but it means that the theory
behind the "Higgs condensate" gets a boost.
After this short introduction, let's first mention a couple of highlights of the "standard model" and
elementary particles (fermions, bosons). Those subjects will then form section 2.
Section 3 will spend a few words on symmetry breaking and why Higgs (or multiple Higgs) is "likely" to exist.
Then, to conclude this small note, I will present some highlights from "supersymmetry" and SUZY models.
2. A few highlights in the standard model, and elementary particles:
The standard model is a framework describing all known fundamental particles, together with the forces and their carriers,
and how it all originate and evolve since the beginning of the Universe.
It tries "to tie together" all facts around those particles and forces.
2.1 A few remarks on elementary particles:
2.1.1 Fermions: Ordinary matter (quarks and leptons):
What we nowadays consider as "ordinary matter" (like atoms), is made from two basic "types" called
quarks and leptons.
- The quarks form the constituents of the well known protons and neutrons.
So, the latter two, are not elementary particles.
- The leptons are the familiar electrons and neutrino's.
2.1.2 Bosons: Force carriers
Physicists have found that there are four fundamental forces at work in the Universe:
the strong (nuclear) force, the weak force, the electromagnetic force, and the gravitational force.
They quite differently with respect to "range" and "strenght".
- Bosons are said to be the particles that transmit interactions (force carriers).
One well-know example of a boson, is the "photon" which is the interacting mechanism for the electromagnetic force.
Actually, there should be 6 (true) bosons of which 4 (or 5) are confirmed bosons (photon, gluon, Z, W+-),
and 2 more (hypothetical) bosons are expected to exist (namely the Graviton, and the Higgs boson).
If you want, you may say: W+-? So we have a W+ (with positive electrical charge) and a W- (negative charge)?
That is true. But since most articles talk about 4 confirmed bosons (taken W+- together), I will do the same.
To summarize the basic matter particles (fermions), and force carriers (bosons), take a look a figure 2 below.
Notes:
(1) We haven't talked about the "anti-" particles yet.
(2) Actually, when considering the property "colour" charge too, we have 18 quark variants instead of 6.
Fig.2: Elementary particles (anti-particles, and "colour charge" of quarks left out)
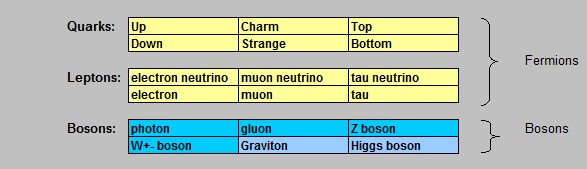
There are many dozens of particles found! But they are not "elementary": you can decompose them into the true
elementary entities. So, figure 2 illustrates what we think is the collection of true elementary particles.
For example, the mesons consists of some quark, and some anti-quark. Again and again, it turns out that
quarks and leptons (and anti-quarks and anti-leptons) are the true building blocks of matter.
The fundamental quarks "up" and "down", "charm" and "strange" and "top" and "bottom", are indeed shown
in figure 2. However, quark theory and chromodynamics, require a "colour charge" (red, green, blue) too
which has been left out. This is not really fundamental to our discussion.
2.1.3 What about the "Anti-particles"?
Section 2.1.1 was not completely "complete". Actually, for every matter particle (quarks, leptons) there exists
an anti-matter particle. Such an Anti-matter particle is the "opposite" in properties, where for example "electrical charge",
and "colour charge", are prominent examples.
So, for example, an electron has an anti-particle partner, which is the "positron", with a positive charge,
completely opposite to the electron.
The same is true for the other leptons: they all have their anti-particle partner.
Again, the same is true for quarks: they all have their anti-particle partner.
But what about a particle like the "anti-proton"? As we know, this particle exists, but just like the "regular" proton,
it's not elementary. It's build from the "anti-quarks", just like the proton is build from quarks.
So, yes, we have an "anti-proton", but it's really the anti-quarks the makes the pudding.
Note: although fermions and bosons are fundamental particles, many articles will once in a while refer to "hadrons",
"baryons", and "mesons". Don't worry: these are all composite particles.
Hadrons is a generic term to denote matter that's build from quarks, so hadrons are composite particles,
and it is a general term. The following hadrons are real composite particles:
⇒ Baryons, for example, are our well-know protons and neutrons, which are "three quark combinations".
⇒ Mesons (like the pion) are intermediate mass particles which are made up of a quark-antiquark pair.
Fig.3: a proton and antiproton
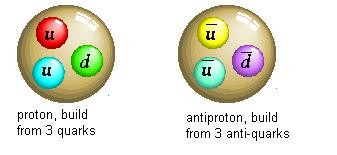
When a particle and an anti-particle "meet", they destroy each other, giving pure energy and
energetic force-carrier particles (bosons), such as gluons, photons or Z-bosons.
So, if for example a electron and positron annihilate, a powerfull gamma-ray will result.
This phenomena is remarkable: a particle and antiparticle give rise to bosons, while in other cases, a boson like a photon
can (in some circumstances) result in an electron and positron pair (pair-forming).
In high-energy physics, using for example particle accelerators which let particles collide, anti-matter may be produced.
Ofcourse, these sorts of events occur everywhere in the universe (stars, supernova, near black-holes etc..); it's just natural.
However, it's still somewhat of an unsolved mystery why the universe is dominated by matter, and why the abundance of
anti-matter is so low.
There is an asymmetry between matter and anti-matter. Why, ultimately, is the world made of matter and not antimatter?
It might be due to "electroweak baryogenesis", which fits the standard model quite well. More about this later.
2.1.4 Fermions: half integer spin, Bosons: integer spin:
There is another difference between fermions and bosons. It's their possible "spin" values,
and the consequences thereoff. The notion of "spin" will be explained in a minute.
A fermion is (defined as) any particle that has an odd half-integer spin (like 1/2, 3/2, and so forth)
So, our Quarks and leptons have an half-integer spin. We already know these are Fermions.
Quarks and leptons are the fundamental (elementary) particles, which we cannot (as the standard model says up to now),
decompose in even more fundamental particles.
However, even non-elementary particles may have an half-integer spin, so they are fermions as well, like
for example the proton. But remember, these are not elementary particles (the quarks and leptons are).
Likewise, a lot of other composite particles may have an integer spin (like 0,1), and then they classify
as being a "boson". As an extreme example: in a metallic lattice, two electrons (leptons) may "pair" up,
in a certain extraordinary case, by which they collectively have spin 0, and that pair then acts as a boson.
As another example: a composite particle, like a 4He atom, always has spin 0, so it's a boson.
But remember, we have 6 "true" bosons (as listed in fig.2) which are the force carriers.
Now, the following is very remarkable (and fundamental):
- Fermions obey the Pauli Exclusion Principle and therefore cannot co-exist in the same state
at same location at the same time. Only one fermion can occupy a particular quantum state at any given time.
- Bosons can occupy the same quantum state. They can occupy the same place in space, with the same
quantum properties. The wave functions are symmetric under particle interchange, and they are allowed
to be in the same state.
In some extreme cases, (composite atomic))bosons can condensate, as if it's one super-sized atom.
Note: What is spin?
That's not a simple question. If we can imaging a fundamental particle as "spinning", we can visualize
that a certain "angular momentum" is associated with that paticle. But this propery is "quantized", or, in other words
it can only take certain discrete values. Now, in the framework of Quantum Mechanics, "discrete values"
of other observables are not uncommon. Many observables, like quantum spin, has no classical counterpart.
Sometimes, it just makes it quite hard to understand such an observable.
We will not spend too much words on "spin", but there exists some deeper relation of "spin" with spacetime,
because it relates to how "algebra of rotations" acts on this property.
It's still not understood completely. It has "to do" with the metrics of spacetime, since Galilean or
relativistic transformations/algebra are today common means to deal/describe this property.
2.2 A few remarks on fundamental forces:
Say, up to 1850, physicist believed that forces worked instantaneous, so, for example, an electrically charged
object, influenced another electrically charged object directly, without delay.
Ofcourse, in later periods this assumption was disproved at countless experiments.
It was not for long that the notion of a "field" entered the arena. This field, is some sort of "a change" in the space
around the object. Especially, the work of Maxwell (electrodynamics) contributed to that view.
The concept of a "field" remained important, and is good way to explain how objects interact and how forces works.
Still, it is realized that it cannot be a complete picture. Like so many things in physics, often a dualistic view
is needed. One famous example ofcourse is the "wave-partice duality" which is demonstrated in Quantum Mechanics.
Equivalent to a "modern view of the field", is describing the interactions between the matter particles, using "gauge"
bosons, which are the "force carriers".
So, forces are transmitted by "force carriers" which are our gauge bosons. For example, the photon
transmits electromagnetism, while W and Z bosons transmit weak interactions.
The two views, that is "field", and "force carrier (boson)", are both unavoidable.
As a simple example: high energetic radiation behaves as a field in many experiments. In other occasions,
like the Compton effect, the field gets synonym to a boson (the photon), a particle even capable in transferring momentum
to an electron. Actually, the best description of a photon then is: it's the boson that emerges when a field interacts
with a matter particle (like the electron).
High Energy physics experiments, have revealed some of the other bosons too, like the W and Z bosons.
This was an incredable succes for the Standard model, which predicted those bosons. The prediction followed from a rather
succesfull attempt to unify the "electromagnetic interaction", with the "weak interaction" into
the "electro-weak" (unified) force.
This unification happens at sufficienly high energies (temperatures) which can be realized in highenergy particle accelerators.
Both the electromagnetic and gravitational force, are long-ranged (likely to be "infinite"). The gravity between
elementary particles is extremely low, but the electromagnetic force is very relevant.
The strong interaction, acts between quarks, using gluons as the force carrier. It's very short ranged (about 10-15m)
I think, whatever your background is, you probably have a reasonable idea about those three fundamental forces, especially
gravitation and the electromagnetic force.
Since the "weak interaction" might be not so familiar, and since it will play a role in chapter 3, we will
spend a few words on this specific force.
The weak interaction is very short-ranged too. It plays a very important role in the decay of particles, like
for example in the decay of a neutron (the socalled Β decay)
Also, it's several orders of magnitude less "in power" compared to both electromagnetism and the strong interaction.
As we will see in chapter 3, the W+ - bosons, and the Z boson, are involved, which all three
are very "massive". Later on, we will see how this "high mass" is coupled to the "short range" of this force.
Here is where Higgs will come in, as we will see later on.
Note:
Even without any unification considerations, you might suspect there is some relation between the weak interaction,
and the electrodynamic interaction. The force carriers of the weak interaction, W+-, are electrically charged
and experience an effect in an Electromagnetic field.
As said before, the Standard Model says that the electromagnetic interaction and the weak interaction,
are two different aspects of a single electro-weak interaction. The unification will occur at very high Energy.
In the process of symmetry breaking, where the single electro-weak interaction "breaks" into
electromagnetic interaction and the weak interaction, the Higgs field plays an important role.
Some people regard the finding of Higgs, to be a test for the validity of the Standard Model.
But even if the Higgs field is found, is can only be part of the solution. Remember, we have four fundamental forces today,
and at "ultra-super-high" energies, it's suspected that today's manifestations of forces,
all merge into one force: also called "Grand Unification".
The figure below illustrates the known force carriers, together with the elementary- and composite particles.
Fig.4: Force Cariers and known forces, and know elementary particles.
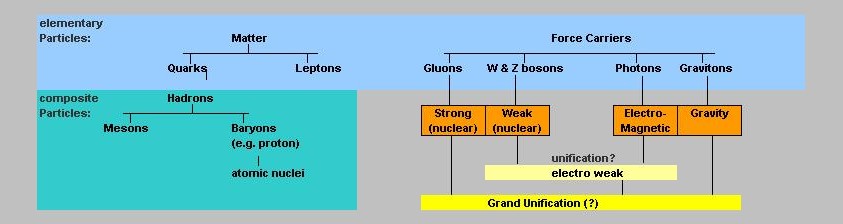
This chapter was a bit factual in nature. It more or less gave a simple overview of known particles and forces.
It did indeed explained a couple of things, but many questions still remain, like:
- Why and how should unification of forces occur?
- Where does "symmetry breaking" comes in?
- Why seems there to exist an asymmetry between particles and anti-particles?
- And, how exactly does the Higgs field comes in?
Anyway, without the facts as presented in this chapter, it was probably more difficult to proceed to the next one,
where we shift focus to symmetry breaking models and Higgs.
Up to now, the Standard Model sounds "pretty good". It should be something as a theory that fits all
particles and forces, and how they originated. But no: there are still many difficulties. For example, to reconcile
Einsteins General Relativity with Quantum Mechanics, has turned out to be a true "brain crusher".
And there exists even many more "difficulties". So, it's not a theory that "fits all" right now.
A handfull of physicist don't even like the concept of a "Standard Model", due to several reasons.
It's probably fair to say that most active physicist, view the Standard Model as a "working" principle,
a sort of set of "insights", which gets refined at every major discovery, and, up to now, was remarkably succesfull.
But the Standard Model already has a sort of "follow-up", namely models which takes "super-symmetry" into account,
like the "(Minimal) Supersymmetric Standard Model".
3. Why Higgs?: A few notes on symmetry breaking, and the Higgs field
3.1 A Pictorial Description:
Ever noticed that you can throw a little rock with high speed, and much further away then, say, a heavy brick?
Ofcourse you do! The mass of the brick limits how far you can throw it. And a very heavy brick,
might even fall just inches before your toes (if you're lucky).
In nature, it might work quite "similar", although the analogy must not be pushed too far.
The force carrier of the Electromagnetic field, the photon, has no rest-mass: It zips around with "c",
while it's range is unlimited.
On the other hand, the carriers of the short-ranged "weak interaction", the W+, W- & Z bosons, are very heavy!
These bosons have been found at experiments in CERN, and have masses in the order of 80 GeV/c2,
which indeed is very heavy. A key point now is, that we note that the "range" at which the weak interaction operates,
(in other words:the bosons), is extremely short.
Why, with the (rest) mass-less photon a long range, why with the W and Z bosons a short range?
Is the analogy with the light- and heavy stones applicable here too?
The force carriers may be regarded as virtual particles. Anyway, it's very reasonable to assume that the
Heisenberg uncertainty relations are in effect here as well. Here, the relation ΔE . Δt > h/2
is important. If a "heavy" particle emerge (from the vacuum), thus with high energy, the corresponding "time span"
must be short. This short time, relates to the "short range" of this carrier.
Note that we are not "mis-using" Heisenberg, because the boson appears, borrowing energy from the vacuum so to speak,
possible only for a "certain duration", which justifies the appliance of the relations.
Indeed, at some point in history, the theoreticians came to the idea the the mass of the "heavy" bosons is just a property
of the vacuum, how weird that may sound when you first hear of it.
Using this idea, it's quite "natural" to assume there is an "all-existing" field, responsible for associating mass
to particles. Since it's a field, a boson (as an exponent) needs to exists as well: that's the Higgs boson.
The key point this "pictorial" description tries to tell, is that we know that the W+, W- & Z are very heavy.
And we also know that the associated "range" is very short ! So the vacuum is "dragging" those bosons dramatically.
This drag is what we know as mass. So that's why they are so heavy and short-ranged!
3.2 A few words on symmetry and invariance:
True scientific papers are very hard to read. And even some popular articles can be quite an endavour too.
The subject is very wide, and you can view it from different angles.
A potential problem are the different technical descriptions, which are indeed related,
but have different meanings, like "gauge invariance", "symmetry" and "supersymmetry".
It's probably best to leave in-depth discussions of "symmetry" and the like, to philosophers and theoretical physicists,
but it's in order to spend a few words on some of those terms.
⇒ Symmetry:
I hope that in all of the above in this note, you may have understood that one of the deepest principles
of nature seems to be that the breaking of an inherent symmetry accounts for the matter and forces
we see today.
So, it is suspected that early in the history of the Universe, a "supersymmetry" was in effect. For this reason,
most physicists in the frontlines of science, don't think that "one Higgs" found, will solve the problem.
Indeed, in the context of the "famous" Higgs field/Boson, the discussion is limited to the process of
symmetry breaking where the single electro-weak interaction "breaks" into electromagnetic interaction
and the weak interaction.
Thus, a more fundamental step would be to unite all forces into one description at superhigh energies, as was
probably present in the earliest phase in the Universe.
But, the smaller step is element of the large step (supersymmetry), so finding, or not finding, (a type of) Higgs
is very relevant for the foundations of physics (and other disciplines as well like Cosmology, Philosopy etc..).
⇒ Invariance:
In physics "gauge invariance", actually is a form of symmetry.
Suppose you discovered (what you first think) is a fundamental physical "formula". But, some time later, you found out
that it only applies in your local neighbourhood, then surely it's not "fundamental"!.
One essential verification of a universal law, is that it should be invariant from your frame of reference.
So, if you for example rotate coordinates, the laws should not change fundamentally.
Also, inherently, if a law stays invariant even if transformations are applied, it's actually a good test for that law.
Not all things in physics are perfectly invariant, but when it comes to fundamental particles and forces,
something called "unitary symmetry" (charge, isospin, color) should be in effect.
I mean, something like electrical charge of an electron should be the same everywhere.
The same should be true for fundamental theories. They should be the same in every frame of reference, everywhere.
Whether you replace coordinates, rotate, or inverse a physical system against some origin, the fundamental interactions
should not change.
A long time ago, when the fundamental laws of Electrodynamics were studied under transformations, the essence did not
changed at all, and to express that fact, the term "gauge invariance" was used for the first time.
Nowadays, generally, whenever fields and force carriers are studied, the invariance is expressed by "gauge invariance".
⇒ Asymmetries:
This is an important subsection.
As of the fifties from the former century, several asymmetries have been found, both due to theoretical work,
and experimental observations
One remarkably asymmetry is, is that the "weak force" seems to have a sort of "preference",
as if the "dices" it uses, are biased. Another strange asymmetry is the abundance of matter over anti-matter.
We already have spoken of theories which are invariant under transformations.
One certain transformation is "mirorring" which creates the mirror image of a physical system,
comparable to what an ordinary mirror does.
It's referred to as "Parity (P) symmetry". You may also see this Parity (or space inversion) as the reflection in the origin
of the space coordinates of a particle or particle system. This inversion should not change the interactions between the
particles in a fundamental way.
With all physical events observed until the fifties of the former century, the symmetry really worked !
For example, electrodynamical events, or gravity, obey P symmetry.
A second rather special operation is "Charge conjugation". Here, in a physical system, we would replace every particle
by it's anti-particle, and the net result should be, that the fundamental interactions do not change at all.
For years it was assumed that charge conjugation and parity were symmetries in effect in elementary processes,
determined by the electromagnetic, strong, and weak interaction.
For example, if you mirror a nuclear process, the same effects are observed.
Now, if an event violates Parity, or Charge conjugation, it's referred to as "P violation" and "C violation".
If both happens at the same event, we evendently will speak of "CP Violation".
It's still not fully explained, but the "weak interaction" which as we know is involved in decay processes,
exhibits "CP Violation", which has been confirmed experimentally by observing meson decays.
This is more strange than you might think at first sight. It effectively means that the mirror of the event
shows a different decay (different numbers of different decay components) than the unmirrored version of the event.
It's still puzzling up to this day, for example, why don't we see CP violations at the strong interaction?
Anyway, different lines of thoughts emerged, like for example postulating a fifth fundamental force,
namely the "superweak" interaction.
⇒ Sponteneous symmetry breaking:
When for example, the force carrier of the "Electromagnetic interaction" (the photon) interacts with an electron,
the electron (as a particle) stays the same.
Also, with the "strong interaction", where the force carrier is the gluon, interactions between quarks will be in such
a way, that the underlying symmetry stays the same.
Now for the weak interaction: It really change the particle (fermion) involved in emitting or absorbing a W- boson.
Suppose we take a look at the decay of a neutron. Here, the Neutron{up,down.down} transforms to a Proton{up,up,down}
by emitting a W- boson. Ofcourse, the W- "lasts" only for an extremely short time and it's corresponding range will be
extremely short too.
Why isn't the same sort of symmetry present with the Weak interaction?
Also, the photon has no mass (restmass). It's very likely that the gluon has no mass too.
But with the weak interaction, the W+- and Z bosons, are very heavy.
Why is that asymmetry present if we compare the masses of the force carriers between the strong- en elctromagnetic
interactions on one side, and the weak interaction on the other side?
The weak interaction has shown to have a "preference" (see the section above) which is shown by CP violation.
Why so?
As a modern explanation: is is believed to be possible for a physical theory to have a symmetry that isn’t reflected
in the current state of the system which this theory describes.
If this is the case, physicists often say the the symmetry is spontaneously broken.
As we already often have seen in this note: the symmetry is believed to be restored at high energies, where the
electromagnetic- and weak interactions, unify in the "electro-weak" interaction.
For our discussion, all what's mention above will do for our small note dealing on the Higgs field.
Only one thing more, might be of interest! Remember I said it's actually strange that matter dominates
above anti-matter? Although far from proven, a certain "bias" (a sort of CP violation) in the early phase of the Universe,
could have been responsible for matter to be produced a little more often than antimatter.
So, when matter and anti-matter "cancelled out" at a later moment, a net result of matter still remained.
Development of these sort of theories, are currently still in progress. Actually, it's quite "hot" stuff.
Hope you have found this short, and very simple note, to be "informative"!



