A simple note on Artificial Intelligence, Machine Learning, and stuff.

Date : 5 October, 2018.
Version: 0.0
By: Albert van der Sel.
Status: Just started.
Remark: The most simple note on AI, DL, ML, and stuff, in this Universe (and others too).

I like to try a simple note on these subjects. It's exciting material in itself, but that is ofcourse no garantee
that I will produce "something useful" ofcourse.
Indeed, it's only "Albert" at work here.....
While it is still under construction, the text might be a bit freaky at places, and certainly incomplete.

Artificial Intelligence (AI) is usually regarded to be a broader domain (or area), than Machine Learning (ML),
or Deep Learning (DL). Indeed, since the very early times of computing, ideas of AI slumbered around,
which probably condensed into more substance since the second half of the '50's.

So, AI started out decades ago. There are a large number of subfields, as you may also think of sensors/perception,
recognition, algolrithms to discriminate essential information from bulk data, algolrithems which
emulate a human interaction, Robotics using AI etc..

It's quite reasonable to say that ML/DL evolved from AI. Hopefully, that will become clear later this text.
Activity in ML/DL, is much more recent than AI, where the interest probably was much boosted since 2000 (or so),
and it seemed to have accelerated since 2010 (or so).
Although some early ideas also originates many decades ago (1960's).

In general, a consensus exist that the three area's (more or less) relate to each other
as shown in figure 1.

Fig. 1: Highlevel view on how AI, ML, DL relate to each other (or their scopes, so to speak).

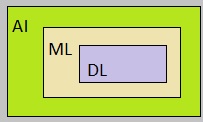
Source: My own Jip and Janneke figure.

Ofcourse, a reasonable description of AI/ML/DL should be tried to formulate right now. However, I wait a bit.

One main theme in ML is, that a "machine" can find a solution for a new situation, based on former "samples",
or former experiences. This then, can indeed be regarded as "learning".

Example (just an example from some subfield in AI):

Below example, must be viewed (sort of) as a "pseudo case" which shows some features of
of a neural network, but avoiding the complexities which are present in reality.

Let's start with a very simple example of ML, as it could be implemented in code, or hardware.
Ofcourse, later on, we will see some facts on (un-)supervised modes, vectors, predictive functions, matrices and stuff.
Maybe it surprises you, but matrix calculus can also be one such important component.

Here, the term "machine" must be interpreted in the most widest sense. That is: a machine (computer),
or just some code, etc..

Many techniques are used, and under development in ML/DL. One such arena is "neural networks".

By the way, referring to figure 1, you might infer that AI does not equate to a neural network.
A neural network is "just" one technique used in AI, and especially in ML/DL.

One simplified implementation might be a sort of mesh of nodes, organized in layers.
Each node, or also called "neuron", has a number of inputs, and a number of outputs.
Usually, a variable "weight" is associated with each input. A specific weight attributed to a specific input,
determines the relative importance of that particular input, for the determination of the output.
The weights are tunable, and might be properties of the neuron itself, or determined by an external agency.

So, an example neuron has 3 inputs, and one output. Keep in mind that in general a neuron
might have "n" inputs and "m" outputs, like n=3 and m=1, or n=1 and m=4, or n=3 and m=20 etc..
With n=1 and m=1, it seems quite hard to knot neurons together in a mesh.
However, at this moment in this text, there are no constraints in effect.

Usually, the output of a neuron is thus determined by the weights of the inputs (in some way), but apart from that,
it's possible that a "treshold" is defined too. This means that the combined inputs must be equal or over
a certain treshold (a certain real value), before any output is activated.

Such a treshold is often "rearranged", and renamed, in something called a "bias". It's sort of the opposite
of a treshold. If a treshold is low, it's very likely that there will be output, having certain inputs.
Using the new convention: if the Bias is high, it's very likely that there will be output having certain inputs.
Just like a treshold, the Bias is a measure for the value, determining that output will occur.

Now, there usually are several layers in such neural network, and often you can find an input layer,
one or more "in-between layer(s)", and an output layer.
Again, at this moment in this text, there are no constraints in effect.

Fig. 2: Simple illustration of a neuron mesh. It could be hundreds or thousends of nodes.

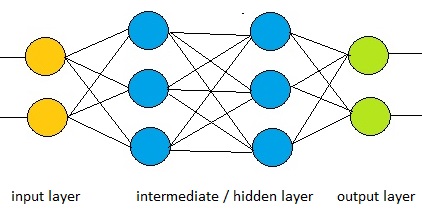
Source: My own Jip and Janneke figure.

The simple figure above, suggest a "one way" direction of signals. This is not always true,
depending on the type of neural network.

As it turned out, with the right setup, it is possible to "feed" the network with training examples,
while carefully tuning the weights and biases in the process. If this worked out, it is possible
that the system from then on, take correct decisions on it's own, when different inputs are provided.

There exists many code examples, e.g. in Python, which demonstrate a neural network
in a way (more or less) as described above.
Ofcourse, also large libraries exists with all sorts of implementations, under various development platforms.

Now: what makes it work? The learning that is...

There exists quite a few neural network variants. This is a topic for a later chapter.
They also differ in the effiency in "learning" for certain tasks, and how it is implemented.

One implementation is using "backpropagation". We knows that the nodes have "weights" defined,
which are tunable (or adjustable) parameters.

If we indeed started out with feeding "training samples" to the system, then we know of the inputs and the desired outputs.
This makes it possible to compare the states of the inputs/outputs compared to what we actually hoped to find.
One method can be this: By applying corrective "differentials" to the weighting functions, it is possible
to let the system work more accurately, in an iterative way, as we work through our training samples.

Those differentials are just those from mathematics. A differential already means the ratio of a small variation
in a variable, and the function which depends on that variable, like in "dy/dx".

In other words, by applying those corrective "differentials", we get closer and closer to our goal.

Then, hopefully (and already proven in many setups), we have learned the system how to tackle new problems.

This is high-level talk ofcourse, and is only valid to convey an impression on how things might work.
So, this example is not fully "exact".

Indeed, all mechanics need to be explained ofcourse. But in a nutshell, we have an idea how a AI system
might work in reality. The example above, is counted to be in the realm of ML, which ofcourse itself is a part of AI.
It's true that neural nets/learning capacity is very important, in many fields of AI.
Or, maybe it's more correct to say that machine learning, thus ML, is very important, in many fields of AI.

I think that stuff like the example above, is pretty cool. However, the formal theory of ML might be percieved
at times "as not so unbelievable cool", since quite a bit of math is required.

To get into AI is impossible in a simple short note as this one. My goal is then only, to provide a microscopic,
and high-level overview on a selection of essentials in AI.

About this note:
If you are already quite familiar to AI, then this note is of no relevance to you.
However, if you are "new", this note might provide some relevant pointers (I hope).

1. A few words on Robotics (using AI):

One area of AI might be called "robotics". Indeed, often physical robots are involved, but this landscape
is quite wide too.

Fig. 3: Simple illustration, trying to "position" robotics (physical autonomous robot) in AI.

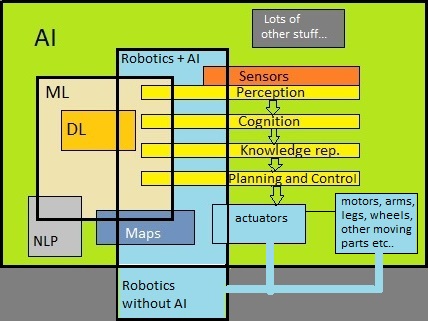
Source: My own Jip and Janneke figure.

Figure 3 is far from "terrific". Indeed, whatever figure you will find, it will never be fully satisfactory.

Note:
Figure 3 suggests that Robotics is part (or a subset) of AI. Many folks say that AI and Robotics are seperate,
and just partly overlap. This shared area then deals on Artificial Intelligent Robots.
I only refer to Robotics in this note (and in figure 3), to be that subfield which describes Artificial
Intelligent Robots (using AI).
Indeed, many Robots (like in many industrial settings), just perform repetitive actions, and do not require AI at all.

There are many ways to distinguish between types of Robots.

- The "common industrial robots", you can find in assembly halls and the like, often do their work in a very precise,
but repetitive way. These are the robots, you can find in for example in a car assembly hall.
Another way to describe them is using the term "preprogrammed robots". All their actions are the result
of a preloaded program, which fully defines all their interactions.
I would like to say that their "degrees of freedom" is fixed (or at least limited) for a certain program.

- "Autonomous Intelligent robots" are the ones we are interested in. They operate without human control,
and often are capable of detecting and interpreting their environment.
Especially here, AI comes into play, since such robots might even learn their environment
and might make independent descisions.
I would like to say that their "degrees of freedom" is not fixed.

There are many other ways to discriminate between types of robots, but for this note, the description
above is good enough. Ofcourse you may also argue that Robots in the form of code, exists too.
This then results in the statement that we have physical robots (with software), and "code only" robots.
However, most folks see such intelligent code, using AI algolrithms, as to be part of AI, and not Robotics.

For a physical autonomous intelligent Robot, the figure tries to illustrate that "perception" and "recognition"
are the first stimula for most of such robots. Suppose that such a robot must traverse a room, where obstacles
are present too. Then, seeing what's in the room, and a form of recognition (e.g. of obstacles), will affect
later actions. As you may see in figure 3, often "knowledge representation" might be part of the intelligence too,
since it might recognize an object as a chair, or Human.
Other parts in such chain might be "planning" and "control". At a certain moment, movement will start
and continue, which collectively is taken care of "actuators" (like motors driving wheels, or legs etc..).

Ofcourse, "seeing" the World, is a starting point. Sensor technology is important, to say the least.
"Tactile sensors, or "optical distance (proximity)" sensors, or camera's, or video sensors,
or otherwise, is a starting requirement for the degree of accuracy of perception.
Assessment of object properties, intelligent manipulation etc.., is then stimulated by recognition.
Here a sort of ML might be implemented, or another sort of Environment reconstruction and mapping is present.

In a nutshell, the above tried to illustrate the components visible in figure 3.

The challenges in the corresponding fields are quite large. For example in "perception": if you try to learn
a ML based module involved in "recognition", then feeding it static 2D images will usually not suffice,
since a visually based moving robot, probably perceives a continuous change of input, in reality.
However, snapshots of images might be used, or a more much advanced procedure.

Figure 3 also shows a simplified archetype for a Robot having a certain degree of Artificial Intelligence.
The fields Perception, Recognition, Planning and Control, activating Actuators, often play a role.
ML, or other AI procedures, might be implemented in any of the above fields.

However, up to now, ML is mostly applied at the "lower" functions, like in Perception/Recognition,
while other AI implementations might have been applied in the higher functions.

2. A few words on Machine Learning:

Often heared phrases of describing ML:

The capability of a machine to improve its own performance.
The science of getting a computer to act without programming.
Machine learning is a field of computer science that uses statistical techniques to give computer systems
the ability to "learn" (e.g., progressively improve performance on a specific task) with data,
without being explicitly programmed. (the third one comes from Wikipedia).
ML replaces the costly and time-consuming step of acquiring deep data knowledge, with the (in many cases)
easier method of using a (relevant) number of examples of that data. These examples then are the "training set".
The training set is fed to the ML implementation in order to produce a trained "machine" with the main task
of mapping inputs to outputs using other (new, unobserved) data (inputs).

I personally find the fourth one, in a general sense, the most descriptive on ML.

Although the descriptions above, are not hard to understand, any description lives under the burden
of the design choice. That is, in what circumstances will ML operate?

For the latter statement, you can see that the implementations might be different, for different environments.
For example, a robot traversing a room with obstacles, is a different environment, compared to
data analysis on "big data". It's true that different approaches have been constructed, and it is sure
that they will be refined, while newer ones will pop up as time progresses.

What we have seen above, the example of a neural network (NN), is not equivalent to the "whole" of ML.
Ofcourse, a NN can be used in ML, but other implementations go around too.

A sort of common framework has been devised, which forms a basis for many ML implementations (or approaches).
This theory describes some important keywords like "features", "labels", "loss function", "regression" etc..
We are going to see about that in section 2.1.

ML is already in full operation, ranging from businesses, robotics, data analysis, public services, websearch engines,
and ofcourse in science etc.. etc.., in various degrees of complexity.

2.1. A few words on the common framework, and introducing some common terms:

You may think of a Robot (using AI) traveling in a room, with al sorts of obstacles (like chairs etc..).
You may also think of a machine inspecting emails, and deciding which are spam and which are not.

Often ML is done using a statistical approach, and it "seems" somewhat less exact, compared to traditional
engineering where each step is fully known, and is completely documented from a technical and functional perspective.
The tradidional way, may take too long, or cost too much, or is too complex in some cases.

If a machine can learn "on the job" and still produce statistically meaningful results, then this might be a great alternative.
However, in some cases, there must be a certain degree for tolerance of errors.

As you see, the term "learning" is the key idea in the whole of ML.

The statistical approach, however, is somewhat less prominent in "classification problems".

Often people start out to find out the meaning of supervised learning and un-supervised learning ML.

2.1.1 Supervised learning and Un-supervised learning

Suppose you start with N samples, often denoted in the form of the collection:

D={x_n, l_n}_n=1^N (equation 1).

where n runs from n=1 to n=N. The x_n are the "inputs" (or features), and the l_n
are often called the "labels", or the "outputs", or the "results" (based on the corresponding input).

It's called supervised since the training examples are complete, including the labels (outputs).

Ofcourse, the key of supervised learning, is that the examples might lead to a generalization which
makes it possible to tackle new inputs as well.
Not seldom then, a "distribution function" is used (or constructed) of which we indeed hope that it
can be applied to the new inputs as well, leading to meaningful results.
This is why we say that ML is often statistical in nature, since the generalization simply involves
statistical methods.

The inputs (or features) are also sometimes called (random) variables.

Un-supervised learning is the method where we do not have the labels (or the results),
belonging to the original dataset. We then only have the inputs.
So, this is ML which needs to try to find "the red line" which characterizes the dataset.
Or in other words: can we find relationships in the dataset, which we can apply on new inputs as well?

I think it is reasonably easy to make it clear, that especially with supervised learning, that we need
a sort of predictive function, so that, whenever we see a new datapoint x_N+1, we can calculate
(or predict, estimate) the corresponding label (which is the result/output) t_N+1.

Now you might say: "That's a pure statistical approach, isn't it?"
For a large part, yes.

But there must be also something special here. It must be get clear, from the data, that indeed
a reasonable (or actually rather good) assumption can be made (from the data) which justify
such predictive statistical function. This is also sometimes called a "predictor" function.

The possible error, or also named as "loss", must be as minimal as possible.
Since we are looking for a good statistical distribution function, the "loss" will then be
also expressed as a "loss function".

Note:

In some articles, the lower level data, or the "perceptions" (the input) is also often called "features".
However, the "higher level insights" are then called the "labels".
This is still quite in line with what we have seen above. A fact is, that if one study ML from a
Robotics perspective, the latter descriptions are more often used. Anyway, the differences are not World shocking.

So, features equal to input data (for example, perceptions, or raw column data etc..).
Any model which is used at training and delivers some sort of output (text, binary, numbers, whatever result),
are the "labels". Remember that "labels" are used with supervised training models.
At supervised training, a label is associated with a datapoint, like you can see in equation 1 above.

Since the goal is that the model will work on still unobserved data (not the training data), we can
rephrase the goal to the sentence that we need to find the predictor(s) which maps as good as possible
from "feature space" to "label space".

So, if the "feature space" would be called X, and the "label space" Y, then we are looking for a predictor
which maps X → Y, also for new, unobserved, features, which deliver (as correctly as possible),
the labels for these new features.

It's often relatively easy to identify the features, or the input data. However, it's often not so easy
to identify the corresponding labels. We indeed have called it the outputs or the labels, but what do we
want to find anyway? The labels should identify what we want to find.
As a condition: there has to be a real existing relation between features and labels, as we hope to express
in the "predictor".

The statistical character as described above, should not be taken too literally, as covering all ML cases.
That would not be true. In many "classification" problems, a slightly other approach is often taken.

2.1.2 A few words on Statistics.

It's actually possible to distinguish between "classification" problems, where our label "l" only takes on
discrete values, like "1" or "0" (e.g. mail has spam, or mail has no spam). Or, the labels (the output space) are in
a finite discrete set like for example {cat, dog, tiger, goldfish, whale, tree}.
In the latter case, the features might be something like weight and temperature, while the "machine" then does
produce the output based on the inputs.

Or, on the other side, we have data where the labels (the output space) are determined by a probability distribution function,
where the range of this outputspace, looks continuous.

This is all element of the science of Statistics and probability theory.

Suppose you have N numbers, like for example the weight of similar containers. In such case,
you can calculate the mean or average weight, and the variance and the standard deviation.
The standard deviation is a sort average of the deviation of the mean value.
These are all relevant numbers for your dataset of N elements. But the space you work with, is discrete,
since you only consider N elements (assuming that N is not too large).

However, when you consider the lifespan of lightbulbs, and you consider lots and lots of them,
the space you work with (the lifespan of lightbulbs) is getting pretty close to a continuous variable.
Ofcourse, even if you study a million lightbulbs, it is still discrete, but the higher N becomes,
the more it starts to look like a continuous variable.
You can still calculate an average, and a standard deviation.
If you would plot the measurements in a xy diagram, with the "lifespan" on the x-axis, and the number
of bulbs on the y-axis, in this particular example, you would see a "Bell shaped" distribution (Gaussian distribution).

Indeed, in reality, the method of taking samples would make it a workable system, since you cannot
test all lightbulbs on the Planet.

In principle, the data (input) could be discrete or continuous, and the labels (output) could be discrete or continuous.
A training set is obviously limited in the sense of the number of examples.

In ML, often two paradigms (inferences) are mentioned, namely the Bayesian and Frequentist ways to approach
statistics and probabilities. (And, there are even others too.)
This almost touches the "philosofy of Science", since under the hood, it's not too hard, but also not very
trivial stuff either.
In treatments, you will encounter terms like "prior", and "posterior", and several others too.
Why different approaches exist, in a large part has to do with the fact that we probably do not know all of our
data beforehand. Even in the case of a large set of table- or column data: we have not inspected all elements.
This has an impact on the "philosofy" of statistics.

This is just a very simple note, so I will not go into the Bayesian/Frequentist stuff,
and for such a note like this, it does not have much impact at all.
However, if you will study other articles, you will encounter these two "inferences" for sure.

In the text above, we already have seen the two term "classification" and "regression" before.
It's probably good to recapitulate them again:

- Classification is the process to place "output" (labels) into a number of discrete values.
The outputspace is thus a finite discrete set.
Often such space is binary, like {true, false} or {Yes, No} or {1, 0} etc.., or it's a multi-class collection
like {cat, dog, shark, tree}.

- Regression is (often) associated with a continuous valued outputspace. This might for example be
the lifespan of lightbulbs, or length of a trajectory of a particle in some materials etc..
Usually a "probability distribution function" works on the input, producing continuous output.

Folks in AI/ML, often first try to determine whether the problem under study, falls under some
Classification technique, or Regression technique.