In the series: Note 10.
Subject: Differential equations Part 1. (Optional note).
Date : 30 March, 2016Version: 0.7
By: Albert van der Sel
Doc. Number: Note 10.
For who: for beginners.
Remark: Please refresh the page to see any updates.
Status: Ready.
This note is especially for beginners.
Maybe you need to pick up "some" basic "mathematics" rather quickly.
So really..., my emphasis is on "rather quickly".
So, I am really not sure of it, but I hope that this note can be of use.
Ofcourse, I hope you like my "style" and try the note anyway.
This note: Note 10: Differential equations Part 1.
Optional note: not required for understanding the other notes in this series.
Each note in this series, is build "on top" of the preceding ones.Please be sure that you are on a "level" at least equivalent to the contents up to, and including, note 9.
Especially note 5 (How to differentiate and obtain the derivative function) should have been read first.
For a substantial discussion of differential equations, we still miss some essential knowledge.
This note will be a "gentle introduction", named "Part 1".
Then, a few notes down the road (where a couple of more subjects will be presented), "Part 2" will follow.
Chapter 1 describes "sort of", the general environment where "Differential equations" live and operate.
I just wanted to start with this sort of background info. But, if you, after reading Chapter 1, say that it's
too abstract and too formal, then you might be right.
But even if you only get "half of it" (that is, of Chapter 1), then that's good enough for me !
Next, a few nice examples (mostly from physics) will be shown in Chapter 2. It can percieved as rather spicy,
but you only need to browse through it, and see if you can pick up the main line of reasoning.
That is, it would be great if you can see how the differential equations can be obtained, and have a "feel"
for the solutions provided.
Chapter 3 is fully optional, and actually unnecessary to read. It considers a damped 2 mass-spring system,
which is somewhat advanced.
If you follow my notes only to get a quick intro in math, then skip chapter 3. It's not neccessary to read it.
Chapter 1. What are differential equations:
1.1 Different angles on differential equations:
Differential equations are used, and analyzed, in many disciplines, not only mathematics.You may think of for example, biology, meteorology, economics and many more.
However, I think that in especially "physics" and "engineering", it may be regarded as a true fundament of most theories.
Most will say that a differential equation is an equation of some function and it's derivatives.
It may play part in some technical problem, and thus the equation must be solved, in order to find that function (or class of functions).
However, in many cases, if you simply see "dx" and "dy" and some expression of x and y, in an equation,
then that's regarded as a differential equation too.
With repect to the importance of the differential equation and it's solutions, maybe it's a little different a physics. Why?
In essence, in physics, a "differential equation" describes the "dynamical state" of a physical system. We will see some examples shortly.
That general "dynamical state", and the corresponding equation is often exactly what physicists look for.
Once having the general equation, specific solutions can be found for specific situations (initial conditions).
By the way, here you *might* see a difference between an engineer and a physicist. The engineer, generally, wants a solution
for a specific technical problem. The physicist likes to have a general description of a system, as fundamental as is possible.
Physicist have physical systems under study, and are most interested in the "widest", most general,
description of such a system. Now, that might be a "differential equation". Not some particular solution that's valid
for just a certain system, under certain boundary conditions or initial conditions .
For example, the four differential equations of Maxwell, fully describe the whole theory of classical electromagnetism.
That is, there exists ofcourse countless different physical systems that interact "in some way" with electromagnetism,
but the differential equations, although formulated in a very general way, can deliver the "solutions".
Those four differential equations of Maxwell, are viewed as monumental in classical physics.
1.2 Most common descriptions of a differential equation:
I think it's informative, what others often say as to what (in general) a "differential equation" is.But, as we will see shortly, there is quite some variety in different types of differential equations.
But here is what we hear often:
(1):
It's an equation with differentials like for example ∂ y / ∂x or ∂ f(x,t) / ∂t.
Note: Often the differentials "dy" and "dx" are used if the function y=f(x) is dependent on one variable (x) only.
A notation like " ∂ f / ∂x" is often used when the function f(x,y,...) is dependent on more than one variable.
In the latter case, the word "partial" (in the phrase "partial differential") is used to denote that we are differentiating
on that particular variable (like x in ∂ f / ∂x".) However, that rule is not strickt, and I will use both notations.
If (1) is true, we already have seen quite a few of them, for example in note 5 and 8.
If we focus on functions with one variable (thus y=f(x)) the we might have for example:
| ∂ y --- = ∂ x |
2x |
Such an equation can be solved by finding the primitive function, like the primitive of 2x in my example.
If you go through Highschool textbooks, you will see numerous examples of such kind.
Here is another example:
| ∂ y --- = ∂ x |
-x --- √y |
Ofcourse, in the two examples above, you can replace ∂ y / ∂ x with ∂ f(x) / ∂ x (remember, y=f(x)).
(2):
A differential equation is an equation involving an unknown function and (one or more of) its derivatives.
Note that this is a very common statement as well. For example y" + 6 y' - y = 0 then is a differential equation.
The example equation here is the same as f "(x) + 6 f '(x) -f(x) =0, since, as always, "y=f(x)".
(3):
A differential equation is an equation involving differentials, and should adhere to a certain format
where determining coefficients are eliminated. We will see that in section 1.3.
These coefficients determine certain classes of functions, and thus the differential equation would not be a "general" equation.
(4):
A differential equation is an equation that relates a function and derivatives, and where the solution is a specific function,
or classes of functions.
(2), (3) and (4) have a sort of common "red line": it relates a function and it's derivative(s), or it relates the
derivative(s) of a function to an expression with variables in common.
However, most will regard (1) through (4) as valid descriptions of differential equations.
1.3 Multiple variables:
Up to now, we have studied function and relations using one variable, like f(x), where "x" is the variable, y=f(x) depends on.It's (up to now), indeed so, that my notes resemble "standard Highschool math" a bit.
The next note will address functions like f(x,y) or f(x,y,z). Thus functions having more than one variable.
There is actually not so much different here, as we will see (in note 11).
Example 1: Scalar function of One variable:
We already have seen lot's of those functions, for example f(x)=3x2-3, or f(x)= -5 ex.The function "f(x)" is dependent on one variable only.
Example 2: Scalar function of More Than One variable:
Suppose we have the function φ(x,y,z) = 3x2y - y3zActually, there is nothing "special" here. Again, it's a scalar function, meaning that the function values are real numbers again,
just as was the case with f(x).
As an interpretation of such a function: x,y,z can represent a point in "space", and maybe φ(x,y,z)
defines some "field", depended on the points (x,y,z), and it's value per point in space just happens to be 3x2y - y3z
By the way: "scalar" is just another word for "number".
Example 3: Other named variables:
in math, it is customary to use x,y,z etc.. as variables. However, especially in engineering and physics,in most occasions other letters or symbols are used. And most often, those sysmbols reflect the physical reality.
For example: a particle, initially at rest, then undergoes an acceleration. Clearly, the distance covered, depends on time.
In such cases, physicists create formula's and plots, using for example "s" as a measure of the distance, and "t" to reflect time.
Instead of an XY plane with an x- and y-axis, they use a plane using an s-axis and t-axis. But there is no fundamental difference
in comparison with the x and y usage. In fact, if the acceleration is "constant" then "s=at2, which you can
view as equal to the parabola y=ax2 (as of x>0).
With respect to functions using more than one variable like φ(x,y,z): I think it's important already in this early phase,
to know that we may encounter differential equations with different "differentials", like "partial" ones as ∂ φ(x,y,z) / ∂ x, or
∂ φ(x,y,z) / ∂ y, or, as another example, something like ∂ f(x,t)/∂ t.
1.4 Official "Format" of simple differential equations:
A differential equation may contains "differentials", like for example:∂ f(x) / ∂x, or ∂2 f(x) / ∂ x2, or ∂ f(x,t) / ∂t, or ∂ φ(x,y,z) / ∂x.
Often it is required that it has a certain "format". In that format, you have a general type of equation, where all definingcoefficients are removed. The following example will make that clear.
Suppose we have the equation y=f(x)=px2 (and "p" can be any number, defining the shape of the parabola)
Then we know (according to what we have seen in note 5):
∂ y / ∂x = 2px
Take both statements together:
y=f(x)=px2 (1)
∂ y / ∂x = 2px (2)
Then in principle, we can eliminate "p":
From (1), we can find that: p=y/x2
Substitue that "p" into (2):
∂ y / ∂x = 2 (y/x2) x
=>
∂ y = 2y/x ∂x
Or written in a clear and large "font":
| ∂ y= | 2y --- ∂x (equation 1) x |
Upper result is what mathematicians formally call a "differential equation".
It is no more than a result by using both equations (1) and (2), and eliminating "p".
But indeed, it looks a bit different.
There is an amazing thing here. Note that there is no "p" in equation 1.
If I rewrite equation 1 to this one:
| ∂ y --- = ∂ x |
2y --- (equation 2) x |
At any point, we can find the gradient of the tangent line, just by filling in "x" and "y"
So, if we consider the point (1,2), then the gradient is 4.
Amazingly, we do not even have to know the "p" of y=f(x)=px2. Do you see that?
We simply get the gradient, at any random point, from equation 2 (!) That's pretty "wide".
Now, this is important for understanding the "formal" standpoint of mathematicains:
You now that "p" determines the shape of the parabola. Just visualize, for example, y=2x2, or y=1/2 x2, or y=-3x2 etc..
Indeed. The equation y=f(x)=px2 defines all possible parabola with it's nose at the Origin (0,0).
Remember the discussion above? Physicists and mathematicians are most interested in the "widest", most general,
description of a system. Well, here we found one. A differential equation with solutions which are all possible parabola
with it's nose at the Origin (0,0). If you take a specific "p", then you find a specific solution.
But our differential equation, just simply gives the gradient, for all cases of y=f(x)=px2.
Relax, we will not play it that hard. We will never "demand" a very specific format, as you will see in the rest of this note.
For Physics, it is important that a differential equation satisfies:
- It's in a general format, and not just a equation for a very specific solution.
- Describes the dynamic state of a system (e.g. a system in a Force field, and what may happen next?)
- If possible: mathematical format like equation (1), that is, f(x) related to ∂ f(x) / ∂x,
in whatever format (like factors with x and y) both not with a defining paramater for a single solution.
1.5 An example, but famous, differential equation from Physics:
Section 1.5 is "Optional reading", but recommended ! It may "look" difficult, but it isn't.If you do NOT like this section, then just skip it. It's not essential for the rest of this note.
1n 1926, Schrodinger published his time-dependent equation which specifies the evolution of a quantum system (like a particle),
in a Force field (or Potential "V"). It looks like this:
| -iħ | ∂ -- ∂t |
Ψ (r,t) = [ ħ2/μ ∇2 + V(r,t) ] Ψ (r,t) (equation 3) |
No, you do not need to remeber this one. But it's a famous differential equation from the early period of the development of Quantum Mechanics.
Ψ (r,t) represents a Quantum system like a particle, usually thought to have wave-like properties as well.
Ψ is dependent on the position in Space (r), and is also time-dependent (t).
The equation describes the evolution of Ψ (r,t), that is the "change with respect to time", ∂/∂ t, and
the distribution of the wave "in space" due to ∇2, which is a sum of spatial differential operators ∂2/∂x2, ∂2/∂y2, and ∂2/∂z2.
As time progresses, the distribution of Ψ (r,t) changes over all points r=(x,y,z), in a dynamical system (a Potential, or Force field is present).
In one dimension (say "x"), the equation essentially says:
-iħ ∂ / ∂t Ψ (x,t) = [ ħ2/μ ∂2 / ∂x2 + V(x,t) ] Ψ (x,t)
The "i", the "-iħ", and the "μ", are constants, and not some defining parameters (like "p" was above).If I leave them out, for illustrational purposes, then we have:
∂ / ∂t Ψ (x,t) = [ ∂2 / ∂x2 + V(x,t) ] Ψ (x,t)
No, I don't want you to remember the equation. The only thing I want, is that you see that the equation:relates a differential of Ψ on t, to a differential of Ψ on spatial coordinates (in this case only "x").
These are really different sort of coordinates. So, it's not an equation of 'x' or ∂ / ∂x only.
1.6 Most common types of differential equations:
There are some classifications of types of differential equations. These claasifications are rather "logical",and I hope you agree on that.
1. The "order" of the equation:
First order:
These equations contain differentials like ∂ / ∂x, but no higher order differentials like ∂2 / ∂x2.
You may also say that these equations only use first derivatives, but no higher derivatives.
Second order:
These equations contain at least one differential ∂2 / ∂x2 and no higher order differential.
You may also say that these equations use at least one second derivative, but no higher derivatives.
2. Ordinary differential equation:
This is the most common one. Here we have a function f(x), using one variable (x), and the differential equation
only contains differentials on x (like ∂ / ∂x, or ∂2 / ∂x2).
3. Partial differential equation:
Here we have functions like φ(x,y,z), or f(x,t) etc.. where the differential equation uses partial differentials
like ∂ φ(x,y,z) / ∂ x, or ∂ φ(x,y,z) / ∂ y
4. Linear differential equation:
This applies to ordinary- and partial differential equations. Let's focus on ordinary ones only (since that is the most easy one).
When f(x) and g(x) are solutions of a linear differential equation, then (f(x) + g(x)) is a solution too, just as
any sum of such functions.
Almost all differential equations you will see (here, and elsewhere) are linear differential equations.
The basis of this, is the fact that for example the ∂ / ∂x "operator" is linear, meaning that
∂ / ∂x (f(x) + g(x)) = ∂ / ∂x f(x) + ∂ / ∂x g(x)
Note the similarity with the derivative of a sum of functions in note 5.
I will repeat that here:
If:
v(x) = f(x) + g(x)
then
v '(x) = f '(x) + g '(x)
Next, let's turn our attention to some examples.
Chapter 2. Some examples:
2.1 Example 1: Using the technique of "seperating variables"
An example from mathematics, and using the technique of "seperating variables":Suppose we have the differential equation:
| dy --- = dx |
3y-2 (equation 4) |
This is a "first order" differential equation since we only see dy/dx (or f '(x)), and it is also an "ordinary differential equation" (ODE)
since f(x) depends on one variable only. If neccessary: check section 1.6 again.
Sometimes, we can use the technique of "seperating variables", in which we want the y and dy on one side of the "=" symbol,
and having the x expression and dx on the other side of the "=" symbol.
If that worked out then we can integrate both sides to obtain the solution (or collection of solutions). This is what we mean:
If seperating the variables succeeded, then we can try as the next step:
| ∫ dy = |
∫ (expression of x) dx (equation 5) |
You will see what I mean if we try it with equation (4):
| dy --- = dx |
3y-2 |
Trying to rearrange the y, dy, x, dx, we multiply both sides with "dx", then we can rewrite it to:
| dy dx --- = dx |
(3y-2)dx |
We can cancel, or eliminate the "dx" on the left side:
| dy = |
(3y-2)dx |
Ok, now divide both sides by (3y-2), and that will then be:
| dy ------ = (3y-2) |
dx |
yes! We managed to get all y, dy on one side, and the x and dx to the other side.
Now, we can integrate both sides, and that will deliver (in principle) the solution.
| dy ∫ ------- = (3y-2) |
∫ dx |
In fact, it now boils down that we are able to find the primitive of both sides.
The theory of integrating and obtaining primitives, was the subject of note 8.
However, there we not too much exercises over there, so, now I realize I got some extra homework to do,
and extend note 8 a bit.
All in all, if you have followed the "reasoning" here, I am quite happy with that.
For now, for me it's all about the principle on how to handle stuff.
2.2 Example 2: Harmonic oscillator, with-, and without damping.
In section 1.2, we have seen several descriptions of differential equations.One of them was this example: y" + 6 y' - y = 0
I want to see a real-world example of such a format too. So, let's try if we can find a differential equation, in a form
that resembles the one like above, and which really describes the motion of a physical system
in a general format. That would be rather cool.
Figure 1. Simple Harmonic oscillator, with-, and without damping.
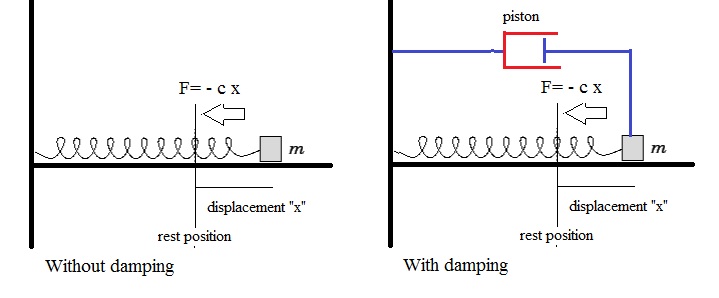
In figure 1, we see a harmonic oscillator, but this time, it's a mass "m" attached to a spring.
In example 3, we will see another example, namely the Pendulum, but fundamentally, that is quite th same principle.
We might have two scenario's: undamped, and damped, where in the latter something like a "piston",
or similar device, will "work against" any change in position.
In most approximations, the magnitude of the damping is linear with the speed of the mass.
This is probably known from experience: For example, the faster you move your hand through water,
the more "drag" you wil feel.
So, the left side in figure 1 represents an undamped ocillator. Here we asume that the friction along
the horizontal axis (the x-axis) is neglectable.
The right side represents a damped ocillator, where a device like a piston, provides a drag against motion.
2.2.1 Undamped mass on a spring
See the left side of figure 2. Suppose, when the spring is in "rest" (equilibrium), the postion of the mass "m" is at x=0.If you strecht the spring, and then let it go, the mass "m" will slide from right to left,
and back again, and repeats the motion with a certain fixed periodicy (or frequency).
In fact, in former notes we have seen similar situations (like the Pendulum, or the discussion
of the sin() and cos() functions in note 4).
Long time ago, Hooke already found that the "restoring" Force that a spring exercises, is linearly dependend
of the extension of the spring (if it's not too large), which is the same as the displacement of "m"
along the x-axis. In other words:
Fr = -kx
where "k" is some constant, depending on the type of spring.The minus sign is due to the fact that the Force is always opposite to the displacement of "m", that is,
if "x" is positive (and we agree on th fact that the left side of the equilibrium position is "positive"), then
the direction of Fr is negative.
Newton's theory of classical mechanics state (among many other things) that universally, it holds that:
F = ma = m d2x/dt2, where "a=d2x/dt2" is the acceleration that a mass "m" undergoes. So:
I agree that if you were not familiar with F=ma, then the example is somewhat more difficult to grasp.
However, you may take just for granted that with any Force on a mass "m", an acceleration is associated,
and the universal relation is "F=ma".
Since, in this case 'ma = -kx', we can write:
| m | d2 x(t) ------- d t2 |
= - k x(t) (equation 6) |
Or, rewritten:
| m | d2 x(t) ------- d t2 |
+ | k x(t) = 0 (equation 7) |
Or, rewritten:
| d2 x(t) ------- d t2 |
+ | k - m |
x(t) = 0 (equation 8) |
Now we can also write this in the familiar "accent" notation for derivatives, like e.g. f '(x), which we have seen
in earlier notes:
x(t)" + k/m x(t) = 0 (equation 9)
This is exactly the "form" of a differential equation we were looking for.Now what about solutions for the Harmonic (undamped) oscillator?
Remember from note 5, that we have for the sin(t) and cos(t) functions:
If f(x)=sin(x) then f '(x)=cos(x) and f "(x)= -sin(x)
If f(x)=cos(x) then f '(x)= -sin(x) and f "(x)=-cos(x)
If you look at equation 8, then sin(t) and cos(t), or combinations thereof, must be pretty close
to the solution of the differential equation we have seen above (equations 6, 7 and 8 are the same).
Remember too, from note 4, that if we would have a pendulum, or mass on a spring, or any other harmonic oscillator,
and we would place a piece of paper, moving with a uniform speed, directly below the mass "m",
we would see the cos(t) function appear. If you would start recording "at the right moment", you would either
see a cos(t) or sin(t) function, just depending on when you start to record the graph.
If needed, revisit note 4 again.
The solution to the undamped mass on a spring differential equation is:
x(t) = a cos(ωt) (equation 10)
orx(t) = a cos(√(k/m) t)
Where "a" is a constant, representing the maximum displacement of the mass "m", when cos(ω t)=1.Also, ω=√(k/m), and represents the frequency of the periodic motion of this undamped system.
It should not surprise you, that the periodicy (T), or frequency, is determined by "k" and "m".
Indeed, "k" is the most important property of the spring (how strong or weak it is), while "m" determines
how much work must be spend to set "m" in motion anyway.
Note: it can't hurt to remember that:
| ω = √ |
k -- m |
If we substitue the solution of x(t) in the differential equation, and just work it out, you would see that
it really is a solution for the equation.
Equation 9 is fully correct, if we displace the spring to the right, and then let go.
That exact point, where I am about to let go, that will define the max displacement, or indeed, "a".
In that situation, which I define as t=0, we get a nice x(t)=a cos(ω t) as the formula of
the motion of mass "m". True, that will be an exact cos(t) function, multiplied by "a".
However, when I define t=0 at, for example, when m is already moving and is, say, at 3/5 of
it's maximum displacement on the left side, we get a cos(t) function with a "phase shift θ", that is:
x(t) = a cos(ωt + θ) (equation 11)
Since physicists are slick people, they favour ofcourse the most simple and elegant solutions.However, there could be some requirement that "time was already ticking", and that we need to find
the position of mass "m" at some moment t=t1.
2.2.2 Damped mass on a spring
This time our Harmonic oscillator has some form of "damping", which gradually lowers the amplitudeof the motion of mass "m". In figure 2, on the right side, you see something that (hopefully) looks
like a piston, that actually is our damping system.
Again, we have as a restoring Force due to the extension of the spring:
Fr = -kx
But that's not all. We also need to take into account the damping system, which in most cases,will display a damping effect which is dependend on the "speed" of the object.
That is: with a low speed, we have a low damping effect. However, if the speed increases, then
so is the damping effect.
In many cases, the "damping" is a linear function of the speed "v", so:
Fd = -cv
Where "c" is some constant depending on the damping system itself.So, this time we have as the differential equation:
| m | d2 x(t) ------- d t2 |
= - k x(t) - cv (equation 12) |
However, the speed "v" actually is dx/dt, or the first derivative of the position. Thus we have:
| m | d2 x(t) ------- d t2 |
+ | d x(t) ----- d t |
+ | k x(t) = 0 (equation 13) |
Or, again we can rewrite that in the following notation:
m x "(t) + c x '(t) + kx(t) = 0 (equation 14)
Now what about solutions for the "damped" Harmonic oscillator?Do you remember note 7 where we discussed the ex and ln(x) functions?
If not, maybe you want to revisit note 7 again.
One remarkable result that we proved in that note was, that:
If f(x) = eax then
f '(x) = a eax
Which also implies that:
f "(x) = a2 eax
A solution to equation 14 (or equations 12, 13), just have to be something like
x(t) = e μ t (equation 15)
Now, the constants like "c" and "k" define the motion of mass "m" too, just like the value of "m" itself.It seems therefore reasonable that the solution must have c, k, and m "somewhere" in the formula.
Indeed, those values "sit" in μ. If we substitute the solution "x(t) = eμt" into equation 14,
then we get the following (which we will not prove here):
m μ2 + c μ + k = 0 (equation 16)
From note 3, we know how to solve quadratic equations, so from equation 16, you are able to find μ yourself.Better physical representation of the solution:
Equation 15, is a mathematical solution, which "fits" in the differential equation.
However if we look at the undamped solution:
x(t) = a cos(ωt + θ) (undamped solution)
Then I really want the "damped solution" to look like the "undamped one", since the damped one might only slowly "die out"and thus for a considerable period of time, resemble the undamped solution closely. Ofcourse, the frequency ω
will differ, since a piston (or similar device) will impact the frequency ω considerably.
You can verify by substituting the following equation of motion, in the differential equation (equation 14),
that it really is a general solution to the damped mass-spring system.
x(t) = a e μ t cos(ω1t + θ) (equation 17)
Now, we really can interpret the preceding solution as a periodic oscillation, of fixed angular frequency ω1,whose amplitude decays exponentially in time due to the e μ t factor.
2.3 Example 3: Another Harmonic oscillator: the Pendulum.
Let's consider the motion of a pendulum. Actually, it's not really fundamentally different from the examples in section 2.2.But it can be nice just to see another physical system, for which the same reasoning applies.
The following analysis is approximately correct, if the maximum displacement of the mass on the rope,
is relatively small. Please take a look at figure 2.
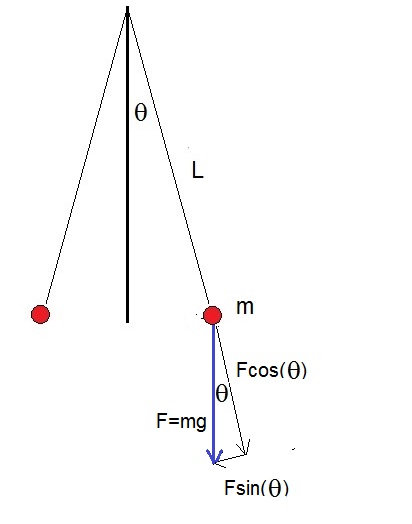
Note the length "L" of the rope and the mass "m", here pictured as a small red ball. Also notice the angle θ,
between the rope and the fixed vertical axis.
The ball swings periodiclly from the left to the right, with a certain fixed freqency "f". Or, you may also say that
a complete "period" (from the maximum displacement on the lef,t to the maximum displacement on the right, and to the
maximum displacement on the left again), takes "T" seconds.
Figure 2. A simple pendulum, where the maximum amplitude us relatively small.
There are several approaches, one of which is quite common in highschool physics, namely using Newton's classical formula F=ma,
or "Force" is equal to "mass x acceleration". Then, that Force is resolved in two components.
In this case, we have a Force due to "gravity", which exactly point downwards. This Force is F=mg,
where "m" is the mass of the ball, and "g" is the "acceleration of Gravity".
I must admit that if you did not know that formula, then what follows is not so trivial anymore.
However, keep in mind that my main goal is simply to get to a differential equation that resembles
something like y" + 6 y' - y = 0. That's all really. So, the physics plays a secondary role here.
In note 12, we go "live" on vectors and matrices. There, you will see that for example a (Force) vector
can be disolved in component vectors, which, when "added", returns the original vector again.
You see in figure 1, that we have done exactly that for F=mg. We now have two component vectors:
Fcos(θ)=mgcos(θ)
Fsin(θ)=mgsin(θ)
Note that mgsin(θ) is the source of the motion of the mass "m".
So, the motion of the ball is due to:
ma = -mgsin(θ) = -mgθ (equation 18)
Note that for a small θ, we have sin(θ)=θ.Now, the following is a bit of physics, I am afraid, but I am going to rewrite the equation above in angular acceleration.
If we look at the "change" of θ, at the motion of the ball, then we can see that θ changes most,
if the orbital speed of the ball (vt) changes most. On the other hand, near one of the two maximum displacements,
the orbital speed is low, and so is the change of θ.
So, the orbital speed (or better: tangential velocity), and the "angular velocity" are linearly related.
Note: actually, the relation is "vt = ω L", where ω=d θ / dt.
It turns out that:
| θ' = |
d θ --- d t |
is linearly related to vorbital. In fact it is vt / L. |
and:
| θ" = |
d2 θ --- d t2 |
is linearly related to at |
Equation 18 can now be rewritten in:
ma = -mgθ =>
m θ" L = -mg θ
On both sides of the "=", we can eliminate "m", and add +gθ:θ" + g/L θ = 0 (equation 19)
or, written differently (in just another notation):| d2 θ(t) ------- d t2 |
+ | g/L θ(t) = 0 (equation 20) |
So, again, in equation 19 we have found a differential equation in the desired format.
2.4 Example 4: Again the damped mass on a spring: the characteristic equation.
In section 2.2.2, which discussed the damped mass on a spring, we found the following differential equation:m x "(t) + c x '(t) + kx(t) = 0
Using good reasons, we assumed the solution to be of the form:x(t) = e μ t
This can be verified by simply substituting the solution into the differential equation:m μ2 e μ t + c μ e μ t + k e μ t = 0
Now, we can factor out the term e μ t:e μ t ( m μ2 + c μ + k ) = 0
meaning that we found an equation to find μ, namely:m μ2 + c μ + k = 0
In this case, it's simply a quadratic equation which can be easily solved in order to find μ.This specific method of helping to solve differential equations is called using the characteristic equation.
Chapter 3. A "two degrees of freedom" system.
This chapter is optional reading.Consider the setup as is shown in figure 3.
Figure 3. Two degrees of freedom, due to the fact we have x1(t) and x2(t).
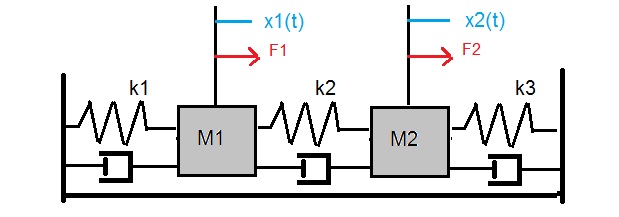
Here we see two masses, "m1" and "m2", and 3 springs, each with it's own characteristic springconstant "k", and
three pistons, again, each with it's own damping constant "c".
Thus we have:
- Masses: m1 and m2
- Springs: with springconstants k1, k2, k3
- Pistons: with damping constants c1, c2, c3
- Postions of masses m1 and m2 in time: x1(t) and x2(t)
- Forces: in fact we have two resultant forces, operating on m1 and m2, namely F1(t) and F2(t)
The only reason why I sketch such a complex system, is to show you that ultimately, mathematicians and physicists
like to describe complex systems using vectors and matrices.
That's really great, as you will see shortly.
Although we haven't touch vectors and matrices yet in this series (probably in notes 12,13, I will),
you will already see some application here.
Let's first try to write down the equations of motion for x1(t) and x2(t).
However, you must have read example 2 above, otherwise I am afraid that this section is pure "abracadabra".
For simplicity, I will start with a system with springs only, and thus first omitting the damping factors (no pistons).
3.1 Equations of motion of a system with no damping (no pistions):
Again, "F = ma=m d2x(t)/dt2" will be our starting formula, which we will set equal toall forces operating on m1 and m2 (just as we did in example 2).
Ofcourse, here the equations will be more lengthy, since we have more components to consider, but really,
there is nothing fundamentally different here.
It's a large puzzle, but if we write it all out, we get the following equations.
Just consider Newton's law on the displacement x1, and next on x2.
This yields the differential equations:
m1 x"1 = -k1x1 + k2(x2 - x1) = -(k1 + k2)x1 + k2x2 (equation 21)
m2 x"2 = -k2(x2 - x1) - k3x2 = k2x1 - (k2 + k3)x2 (equation 22)
Note the " and ' symbols, in order to denote that we are actually dealing with d2x(t)/dt2 and dx(t)/dt.Now, we have x1(t) and x2(t), which define the position of the two masses at any time "t".
In fact, we are looking for the equations which will decribe x1(t) and x2(t), and which
are solutions for the differential equations 21 and 22.
Those solutions will probably not so "easy" as we saw in section 2.2.1. like e.g. x1(t) = a cos(ωt + θ) as we saw in eqution 11.
However, many physicist will first try to "ease" the notation of equations 21 and 22 somewhat.
For that, they use "vectors", "matrices", and "determinants".
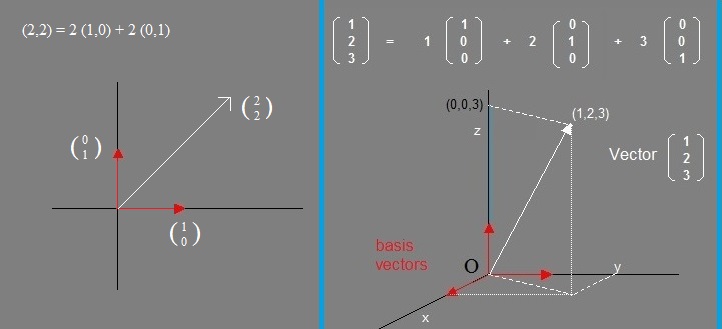
Take a look at this example: A point in the XY-plane, maybe pinpointed by stating the "point" (x,y).
For specific values of "x" and "y", you indeed get a unique "point" in the plane.
An interpretation from vector calculus tells us, that if you define the two basis-vectors, (1,0) and (0,1), where
(1,0) is a basisvector with length 1 along the x-axis, and (0,1) is the basisvector along the y-axis, then we can
represent the "point" (x,y) also as "(x,y) = x (1,0) + y (0,1)".
A few examples of vectors can be seen in figure 4 below.
Figure 4. A few examples of vectors in R2 and R3.
Just like a vector for the point (x,y), we can imaging an abstract vector, namely
( x1(t), x2(t) ), or in short (leaving out "t"), (x1, x2)
where x1(t) plays a similar role as "x", and similar for x2(t) and "y".
But that can be done for the values of the forces F1(t) and F2(t) as well,
and thus yielding the vector:
( F1(t), F2(t) ), or in short (leaving out "t"), (F1, F2)
How does this relate to equations 21 and 22?
Well, you can dividee both sides of these equations by "m1" and "m2"
m1 x"1 = -(k1 + k2)x1 + k2x2
m2x"2 = k2x1 - (k2 + k3)x2
=>
x"1 = -(k1/m1 + k2/m1) x1 + k2/m1 x2
x"2 = k2/m2 x1 - (k2/m2 + k3/m2) x2
We can write that as an equation involving the vectors (x"1, x"2) and (x1, x2):
Figure 5. The 2 mass - 3 springs matrix equation
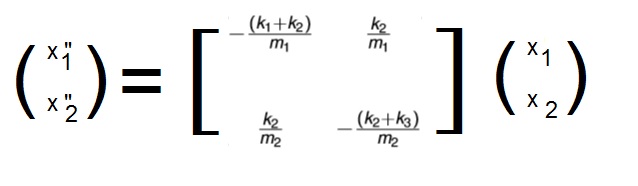
The part between the "[ ]" is called a "Matrix", and in general defines an operation between vectors.
In a very compact notation, we may write equations 21 and 22 as: x" = A x, where "A" represents the matrix.
That compact notation written in full, is displayed in figure 5.