Basic arithmetic/calculus.
In the series: Note 19.

Subject: Equations with exponents and logarithms

Date : 14 November, 2019
Version: 0.5
By: Albert van der Sel
Doc. Number: Note 19.
For who: for beginners.
Remark: Please refresh the page to see any updates.
Status: Ready

This note is especially for beginners.

Maybe you need to pick up "some" basic "mathematics" rather quickly.
So really..., my emphasis is on "rather quickly".

So, I am not sure of it, but I hope that this note can be of use.
Ofcourse, I hope you like my "style" and try the note anyway.

This note: Note 19: Solving Equations with exponents and logarithms.

Each note in this series, is build "on top" of the preceding ones.
Please be sure that you are on a "level" at least equivalent to the contents up to, and including, note 18.
At least, before you start here, take a look at note 7, the "b^x, e^x, and ln(x) functions".

Contents:
1. Very Quick recap exponential functions y=a^x.
2. Logarithmic functions.
3. A very quick recap on working with Powers.
4. Some important properties of Logarithms.
5. Solving equations with exponents and logarithms.
6. The domain for logarithmic functions (for which "x" are they valid?).

1. Very Quick recap exponential function y=a^x.

1.1 A few mathematical observations on exponential functions:

Figure 1. A few examples of f(x)=a^x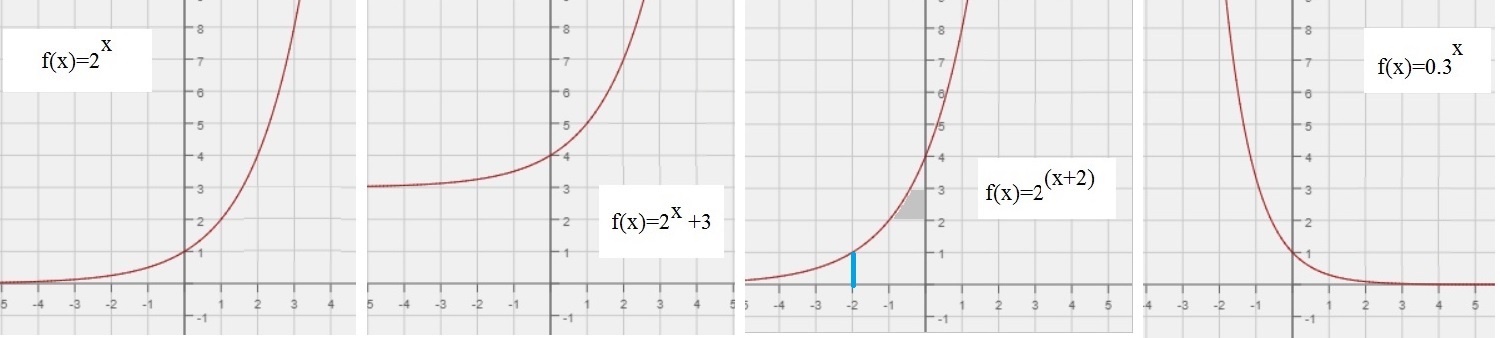

In figure 1, we see 4 examples of the function f(x)=a^x.

Take a look at f(x)=2^x. You can easily fill some x-values, like -1, 0, 1, 2 etc..,
in that expression, to find the corresponding "y" values.
Let's try a few: 2⁰=1, 2¹=2, 2²=4, 2³=8, and 2^-1=1/2.
You can see that the values found, match the graph. Further, it's a rising function, if x increases.

For the fourth figure, the base number is "0.3". You can perform the same sort of excercise, and find out
that it is a decreasing function. For example, for x=2, we have 0.3²=0.3 * 0.3 = 0.09.
So, if x=4, we would have 0.3⁴=0.0081. The function nears "0" quickly, when x gets larger and larger.
But it never actually will be "0", since the line y=0, is it's asymptote.

So, in general, for f(x)=a^x:

- If a>1, it's an ascending function.
- And for a in [0,1], it's a decending function.

But the "borders" 0 and 1, are usually left out. Why?
Well, f(x)=0^x is zero everywhere, and f(x)=1^x is 1 everywhere.
We do not have to leave 0 and 1 out, but they are not so useful as the base number.

-Now take a look at f(x)=2^x + 3. The "3" is not in the exponent. It's just a constant number
added to f(x)=2^x, over all values of x. As the effect, the whole graph is lifted "3" upwards,
compared to f(x)=2^x.
Note, that in this case, the asymptote is the line "y=3".

-If we would have f(x)=2^x - 3, the whole graph sinks by "3", compared to f(x)=2^x.
Note, that in that case, the asymptote is the line "y = -3".

-Now, what if a constant number is in the exponent, like f(x)=2^x+3?
Again you could fill in some typical x values, like -1, 0, 1, 2 etc.., and simply find out, that
the whole function is "shifted" to the left, by three points, compared to f(x)=2^x.
If figure 1 above, you see that happening for f(x)=2^x+2, which is shifted "2" to the left.

-You try that for f(x)=2^x-3 as well, and find that the whole graph is shifted to the right.

You can find more of such examples in note 7.

-Suppose you would have f(x) = -2^x. Then you would find, that it's like 2^x,
but this time mirrored with respect to the x-axis. Then it would be a decending function.

-Next, suppose we would have f(x) = b*2^x, like for example 7*2^x
Compared to 2^x, 7*2^x makes it rise 7x faster. So, a constant factor "b"
before the exponent, makes it rise more steeply, if "b" > 1.

All of the above, are just a few examples of socalled "transformations".

A slightly more general expression for an exponential fuction would be:

f(x) = b a^x

where "a" and "b" are constant numbers, and "a" is the subject of the
exponential power, also called the "base" or "base number" (like the "2" in 2^x.

Again, even a tiny bit more general expression would be:

f(x) = b a^g(x)

where g(x) could be an expression like (2x-6). An example function then would be f(x) = 5 3^(2x-6)

1.2 A different way to write an exponential function:

N = b g^t

In the formula, "g" is often called the base number, but even more often called the "growthfactor".
It has the same role as for example "2" in the equation f(x) = 2^x.

The formula above, is absolutely no different from what we already have seen.
Usually, in math, we use "y" and "x" in our formula's.

However, if something changes with time "t", then we often simply use time as the variable,
(represented by the "t" symbol) to take the place of "x". It really does not matter.
In that case, we do not have an "x-axis", but instead we use a "t-axis".

Secondly, we might replace f(x) or "y" (which are the same), with "N", or "N(t)", if indeed
N is a number that is dependent on "t" (like the same roles like x and y had).

An example is the growth of a colony of bacteria, where the number "N" of bacteria,
depends exponentially on "t".

Especially in researches and articles from biology, sociology etc.., this notation is common.

Note that in a formula like N(t) = b g^t, or f(x) = b a^x, "b" is often called
the "start value" or "initial value". This is so, since when t=0 (or x=0), the exponential
resolves to "1". That is:

N(0) = b * g⁰ => N(0) = b * 1 = b.

Ofcourse, you remember that anything to power of "0", is simply "1". Thus g⁰=1.
Such initial value is most often interpreted as the start value when the observations begin,
like for example the growth of bacteria over hours, or days (or other time interval).

So, often the measurements start at "t=0". But, it could also be so, that folks start
in the year 2007 (starting year), and record the usage of Internet of the inhabitants
of a city. In such an example, a researcher could observe as of 2007, up to 2012.
Then, 2007 is ofcourse not really "t=0", but it is treated like so.

It's important to note that:

N = b, when t=0, which is the initial value (of N).
g is also called the base number, or "growthfactor".

Note 7, section 2, provides some examples of the practical use of the function N(t) = b g^t

Section 1 is just a small recap, of what you already could find in note 7.

The real objective of this note, is how to solve equations with exponential and/or logarithmic functions.
Thus, we need to explore logarithmic functions first.

2. Logarithmic functions.

Logarithmic functions are pretty amazing, and foremost, enormously useful.

2.1 Why do we have Logarithmic functions?:

There are several reasons why we use them.

(1). First, Logarithmic functions are "the inverse functions" of exponential functions.

From former notes, you may remember, that we may have the functions f(x) and g(x),
for which holds that f(g(x)) = g(f(x)) = x. If so, then both are called "the inverse" of the other.

That is, if we first apply f() on x, then apply g() on f(x), then we have x again!

In a graph in the XY coordinate system, then f() and g(), are each "mirrorred" in the line y = x.
Take a look at the figure below. It shows a few examples.

Figure 2. A few examples of inverse functions.

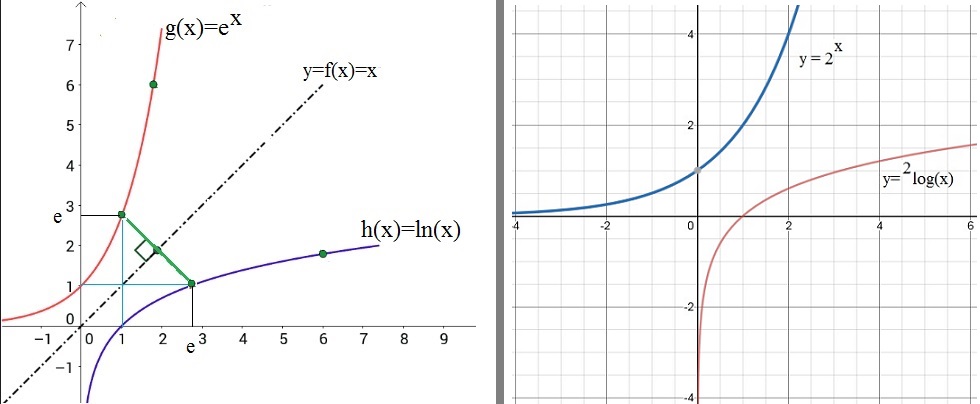
In the figure, you see on the right side, the function 2^x, and it's inverse
function called "²log(x).
The name "log()" may sound a bit weird right now, but I will deal with that in a moment.
Since both are each mirror function (thus mirrored in the line f(x)=x), they are called inverse functions.

So, then it should be true that 2^log(x) is "x" again. The same should be true for log(2^x)=x.
For the statement above, I should make it plausible right now, but I wait a small moment.

(2). Representation of large values.

Generally, if "a" > 1, then a function like a^x, skyrockets to high values, even for relatively
small values of "x". For example the function f(x)=10^x, already has an y value of 1000000, for an
x value of "6".

In some cases, if you mirror such a fast function in the line y=x, then you can still represent it
in a meaning full way, although ofcourse you are now talking about inverse values.
Nevertheless, sometimes the trick works.

(3). Logarithmic functions greatly simplify several classes of calculations, like exponential equations..

Point 3 will indeed be thorougly demonstrated in section 5 below.

Now back to the definition of the Logarithm:

^bLog(x)=y <=> b^y=x

Is this definition meaningful? That is, would the definition b^y = x and ^bLog(x)=y, imply that both
be each other inverse function?
That would be one of the cores, to justify it: The "log" is the inverse of the "exp".
Let's try:

Suppose f(x)=2^x and g(x)=²log(x).

Then g(f(x))= ²log(2^x) = x. According to the definition, this works!

That is:

If:

g(f(x))= ²log(2^x) = x

Then:

2^x = 2^x, which is true, in other words, produces a true statement.

And we only have applied the definition, to find this statement.

Not in all regions,exactly the same notation is used. Let's see for example ³log(x).

In some regions it might be written as:

³log(x) or as: log₃(x) or as: log³(x)

That's not world shocking ofcourse, but it's important to know there are different notations,
which all means the same thing.

To get used in working with logarithms, here are a few examples with just numbers:

⁴log(16) = 2. Indeed, we have 4² = 16 (see also the definition above).

³log(27) = 3. Indeed, we have 3³ = 27 (works again exactly as the definition above).

¹⁰log(10000) = 4. Indeed, we have 10⁴ = 10000 (works again exactly as the definition above).

When you indeed have carefully studied those 3 examples, you should agree that:

^bLog(x)=y describes exactly the same as b^y=x.

The graph of ¹⁰log (x):

The "base", or "base number" is the number that's lifted up, in an expression like ¹⁰log (x).
Maybe it's nice to show a part of the graph of f(x)=¹⁰log (x). See the figure below. Note, that once
the graph takes on positive values (when it gets above the x-axis), it still "rises", but slower and slower,
as x got larger.

Well, that is not strange at all. It's the inverse of 10^x, and when you see that one,
you can see that it is rising faster and faster, as x got larger.

Figure 3. Illustration of ¹⁰log (x).

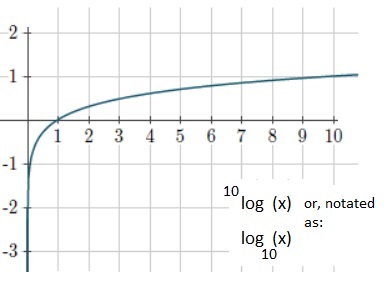
In the graph, you can see that ¹⁰log (10) = 1.

As another illustration: what would be ¹⁰log (100)? The answer is "2".

To understand that, you might also consider it's inverse function: 10^x.
In that case, we have for x=2, the value of 10²=100.
Hopefully can see it all work out, considering that both are mirrors with respect to the line y=x.

But you can also immediately refer to the definition:
If ¹⁰log (100) = 2, then we must have 10²=100, which is indeed so.

The "10 base Logarithmic function" is often used in Calculus, also due to the Worldwide used
decimal number system.

3. A very quick recap on working with Powers.

In case you are really new to "powers" and stuff, you might take a look
at note 1, "arithmetic", where as of section 7, some basics are explained.

This section is extremely small. I just want to make sure, that working with
powers is quite comfortable for the reader.

We have seen exponential functions, like f(x)=2^x, or f(x)=(⅓)^x etc..
These are real functions, and operate over ℝ, that is, the entire x-axis, or all values that
x can attain on the x-axis (the domain is ℝ, all real values).

In the following, we will talk just about numbers, represented by "a", or "b" etc..
We just want to know how to work with powers of different degrees.
So, for example, "a" can be any number like: 1, 5, 10, -1, -17, ⅓, 365, 0.15, 2.5 etc..
Here are some illustrative examples:

3.1 A very quick recap on basic rules for Powers.

Here are a few basic rules in relation to Powers:

Rule 1:

a^p * a^q = a^p+q

Example:

a³ * a² = (aaa) * (aa) = aaaaa = a³⁺² = a⁵

Rule 2:

a^p
-
a^q = a^{p - q}

Example:

a⁷
-
a⁵ = aaaaaaa
----------------
aaaaa = aa = a² = a^7-5

Rule 3:

(a^p)^q = a^pq

Example:

(a³)² = (aaa) * (aaa) = aaaaaa = a^32 = a⁶

Rule 4:

(ab)^p = a^pb^p

Example:

(ab)³ = (ab) * (ab) * (ab) = aaa * bbb = a³b³

The upper overview should cover most, with resepct to working with powers.
However, I like to make sure we are on the same line with "negative" powers,
so that's why we cover that in section 3.2 below:

3.2 Some specifics with "negative" Powers.

When you see this: 5³ * 5²
then you would say, that's no problem, and the answer is: 5³ * 5² = 5³⁺²=5⁵

When you see this: 5³ * 5 ^-2
then there is no problem too. Just follow rule 1: 5³ * 5 ^-2 = 5^{3 - 2} = 5¹ = 5.

Now, it's also important to realize, that an expression like:

1
--
10³

10^-3 (note the negative exponent)

A negative exponent, means that you may also write it as the denominator with the opposite sign of the exponent,
as we have seen above.

Now, if you see something like this:

1
--
10^-5

then it's really equivalent to 10⁵

So, we can also simplify expressions like:

p⁴ * p^-3
-------
p²

p⁴ * p^-3 * p^-2 = (just rule 1) => p^4-3-2 = p^-1 (note the negative exponent)

Most often, the multiplication symbol (like * or x) is left out from expressions.
For example:

qp²(p^-1q^-1 + p³) = qp²p^-1q^-1 + qp²p³ = p + qp⁵

Sure, such an expression as above, is quite nasty. However, it's fortunately no more than following the "rules".
(Who likes to follow the rules all the time?? Not me. However, with math..., it's another story. Follow the rules.)

4. Some important properties of Logarithms:

This is actually a short section too. I just want to list some important properties
of logarithms.

The most important (defining) property is this one:

^bLog(x)=y <=> b^y=x

That one, we already have seen before. For example, in numbers:

⁴log(16) = 2, since 4² = 16.

and, as another example:

⁴log(64) = 3, since 4³ = 64.

The following list of properties, may be viewed as mathematical rules for working with logarithms.

Rule 1:

^glog(a) + ^glog(b) = ^glog(ab)

Now, you probably want me to prove it. That's actually not so very hard....
However, we are going to review an example, to see if Rule 1 works:

Suppose we have a=2 and b=3, with a logarithmic base of 4:

⁴log(16). That will resolve to "2".

⁴log(64). That will resolve to "3".

(You might even take a look at the examples above.)

So:

⁴log(16) + ⁴log(64) = 2 + 3 = 5.

Now let's see what the following will return:

⁴log(16*64) = ⁴log(1024) = 5. This is so since 4⁵ = 1024.

Note: 4 * 4 * 4 * 4 * 4 = 16 * 4 * 4 * 4 = 64 * 4 * 4 = 256 * 4 = 1024.

Rule 1 works !

Rule 2:

^glog(a) - ^glog(b) = ^glog(a/b)

Using again an example, let's see if this is true:

Let's calculate the following. Suppose a=10000 and b=100:

¹⁰log(10000) = 4.

¹⁰log(100) = 2.

Thus:

¹⁰log(10000) - ¹⁰log(100) = 4 - 2 = 2.

Now let's see what the following produces:

¹⁰log(10000/100) = ¹⁰log(100) = 2.

Yes, rule 2 works too !

Rule 3:

n * ^glog(a) = ^glog(aⁿ)

Yes, I could simply demonstrate that rule too, with an example.
However, in the next section, we will get a fair share of examples.

Ofcourse, there are more important properties. We will see those, when we need them
in coming examples.

I think we are ready for section 5: Solving equations with exponents and logarithms.

5. Solving equations with exponents and logarithms.

There exists many "forms" (or formats) of equations.
Let's just discuss a few important ones, and illustrate them, with one
or a few examples.

Most often, the equation has the variable "x" in the exponents, and "solving"
then means finding the x values for which the equation is true.

I just created some examples. Maybe there are some typo errors here and there.
But that is not important. It all revolves around the method, thus on how we approach
the equations. That's the key !

1. Equations using exponentials, with the same base in all terms:

Suppose we see an equation like

a^f(x) = a^g(x) (where a is some number).

Then we may immediately reduce the equation to:

f(x) = g(x)

Why? Well if we would see for example a^x = a³, then the only thing
that would really fit that equation, is "x = 3". It's rather obvious ofcourse, given such
simple example. However, it's valid for complicated expressions as well.

Thus:

a^f(x) = a^g(x) => f(x) = g(x) (usually an ordinary equation).

Example 1:

5^x-2 = 25 => 5^x-2 = 5² => x-2 = 2 => x = 4.

Let's checkit, by filling in "x=4" into the equation: 5^4-2 = 5² = 25.
That's correct.

Example 2:

This is a nasty one. It may take some time, to find a usable approach. But, that's normal.

8^(-2-4x)

1
-------
8^(2x-4)

I would start by saying 8=2³. Then we can rewrite the equation to:

2^(-6-12x) = 2^(-6x+12)

I deliberately skipped showing an intermediate step. It would be great if you could find that.

Now we have everything in the same base number (2). Thus:

-6-12x = -6x+12 => -6x=18 => x= -18/6.

Example 3:

6^x²=6⁴

The base numbers are already exactly the same. Thus:

x² = 4 => x=2 ∨ x=-2.

2. Equations using exponentials and/or logarithms: Part 1.

-In many cases, the basic rule:

"^glog(a) = b then g^b = a" will help us out.

Or read it this way:

g^the_exponent = answer

then:

the_exponent = ^glog(answer)

Or, ofcourse, we need to make use of the rules of section 4.

Example 1:

⁵log(5x-1) = -1

Thus:

5^-1=5x-1 => 5x=6/5 => x= 6/25.

Example 2:

-3 + ⁵log(5x) = -1

Thus:

⁵log(5x) = -1 + 3 = 2 =>

5² = 5x =>

5x = 25 => x = 5.

Example 3:

Solve the equation:

³log(x+6) = 2 - ³log(x)

Set al the log's on one side:

³log(x+6) + ³log(x) = 2

Remember the rule: log(a) + log(b) = log(ab) (see section 4).

³log(x(x+6)) = 2

3² = x(x+6) =>

x² +6x = 9 =>

x² +6x -9 = 0

Such a quadratic equation might have 0, 1, or 2 solutions.
You might see note 3, for solving such equation.

Example 4:

Solve:

¹⁰log(x-5) + ¹⁰(x-1) = 0 =>

We again apply a rule from section 4:

¹⁰log((x-5)(x-1)) = 0 =>

1 = (x-5)(x-1) = x² - 6x + 6

So, we need to solve the quadratic equation x² - 6x + 5 = 0.
Fortunately, you know how to do that !

More examples will follow shortly!

6. The domain of logarithmic functions.

If you look at the basis function

f(x)=log(x)

Then you know that here, x must be larger than "0".
If you wonder why exactly, then:

- log functions are the inverse of the a^x functions, while for those
exponential functions, it holds that y=a^x must be larger than "0".
You know that the inverse functions are mirrored in the line y=x.
So, that's one reason.

-The most important (defining) property of logrithms this one:

^bLog(y)=x <=> b^x=y

For b^x=y, where y then goes to "0", does not work. Again b^x is always >0,

So, for f(x)=log(x), we can say that x must be larger than "0".

Example 1:

Suppose we have f(x)=log(x²-4x).

- What is the domain for this function?
- What are the intersection(s) with the x-axis, if any?

The domain:

We must have: x²-4x > 0.

Let's first solve g(x)=x²-4x =0. This has the solutions x=0 and x=4.
For g(x)=x²-4x, which is a parabola, it holds that g(x) is positive for x<0 and x>4.
So, the domain for (x)=log(x²-4x) is x<0 and x>4

The graph of f(x) looks like this:

Figure 4. Illustration of f(x)=log(x²-4x).

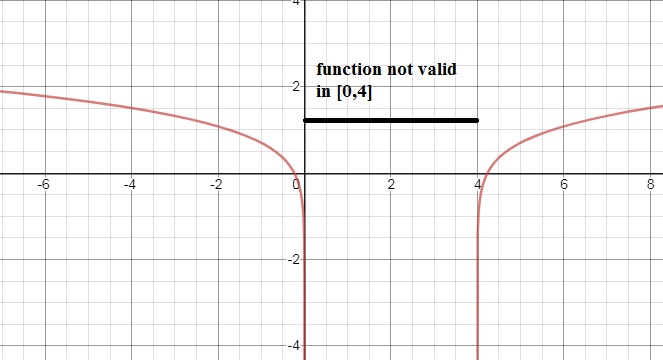
Do not look at the points where f(x)=log(x²-4x) =0. Those are the intersections
of f(x) with the x-axis. That is not the question, actually
So, the x interval [0,4] is not a valid "x" interval for f(x).

Intersections x-axis:

Here we must have log(x²-4x) = 0.

log(x²-4x) = 0 => (x²-4x) = 10⁰= 1 =>

x²-4x = 1 => x²-4x -1 =0 =>

Using the "abc formula":

x= 2+(√20)/2 or x=2-(√20)/2.

Example 2:

Suppose we have the function g(x)=6 + 3*log(8-2x).

- What is the domain for this function?
- What are the intersection(s) with the x-axis, if any?

The domain:

Same sort of story again:

We must have 8-2x > 0 => -2x > -8 => x < 4.

Ofcourse, you can fully "igone" the "6" constant in "6 + 3*log(8-2x)",
since that only represents an translation along the y-axis, of 6, with respect to "3*log(8-2x)".

Intersections x-axis:

g(x)=6 + 3*log(8-2x)=0 =>

3*log(8-2x) = -6 =>

log(8-2x) = -2 =>

8-2x = 10^-2 = 1/100 =>

-2x = -799/100 =>

x = 799/200 (is approximately about 4).

That's it. Hope you liked it !.

Basic arithmetic/calculus. In the series: Note 19.

Subject: Equations with exponents and logarithms

This note is especially for beginners. Maybe you need to pick up "some" basic "mathematics" rather quickly. So really..., my emphasis is on "rather quickly". So, I am not sure of it, but I hope that this note can be of use. Ofcourse, I hope you like my "style" and try the note anyway.

Contents: 1. Very Quick recap exponential functions y=ax. 2. Logarithmic functions. 3. A very quick recap on working with Powers. 4. Some important properties of Logarithms. 5. Solving equations with exponents and logarithms. 6. The domain for logarithmic functions (for which "x" are they valid?).

1. Very Quick recap exponential function y=ax.

1.1 A few mathematical observations on exponential functions:

f(x) = b ax

f(x) = b ag(x)

1.2 A different way to write an exponential function:

N = b gt

2. Logarithmic functions.

2.1 Why do we have Logarithmic functions?:

bLog(x)=y <=> by=x

3. A very quick recap on working with Powers.

3.1 A very quick recap on basic rules for Powers.

Rule 1: ap * aq = ap+q Example: a3 * a2 = (a*a*a) * (a*a) = a*a*a*a*a = a3+2 = a5 Rule 2: ap - aq = ap - q Example: a7 - a5 = a*a*a*a*a*a*a ---------------- a*a*a*a*a = a*a = a2 = a7-5 Rule 3: (ap)q = apq Example: (a3)2 = (a*a*a) * (a*a*a) = a*a*a*a*a*a = a3*2 = a6

Rule 4: (ab)p = apbp Example: (ab)3 = (ab) * (ab) * (ab) = a*a*a * b*b*b = a3b3

3.2 Some specifics with "negative" Powers.

4. Some important properties of Logarithms:

bLog(x)=y <=> by=x

Rule 1: glog(a) + glog(b) = glog(ab)

Rule 2: glog(a) - glog(b) = glog(a/b)

Rule 3: n * glog(a) = glog(an)

5. Solving equations with exponents and logarithms.

1. Equations using exponentials, with the same base in all terms:

af(x) = ag(x) => f(x) = g(x) (usually an ordinary equation).

2. Equations using exponentials and/or logarithms: Part 1.

6. The domain of logarithmic functions.

Example 1:

Example 2:

That's it. Hope you liked it !.

Basic arithmetic/calculus.
In the series: Note 19.

This note is especially for beginners.

Maybe you need to pick up "some" basic "mathematics" rather quickly.
So really..., my emphasis is on "rather quickly".

So, I am not sure of it, but I hope that this note can be of use.
Ofcourse, I hope you like my "style" and try the note anyway.

Contents:
1. Very Quick recap exponential functions y=a^x.
2. Logarithmic functions.
3. A very quick recap on working with Powers.
4. Some important properties of Logarithms.
5. Solving equations with exponents and logarithms.
6. The domain for logarithmic functions (for which "x" are they valid?).

1. Very Quick recap exponential function y=a^x.

f(x) = b a^x

f(x) = b a^g(x)

N = b g^t

^bLog(x)=y <=> b^y=x

Rule 1:

a^p * a^q = a^p+q

Example:

a³ * a² = (aaa) * (aa) = aaaaa = a³⁺² = a⁵

Rule 2:

a^p
-
a^q = a^{p - q}

Example:

a⁷
-
a⁵ = aaaaaaa
----------------
aaaaa = aa = a² = a^7-5

Rule 3:

(a^p)^q = a^pq

Example:

(a³)² = (aaa) * (aaa) = aaaaaa = a^32 = a⁶

Rule 4:

(ab)^p = a^pb^p

Example:

(ab)³ = (ab) * (ab) * (ab) = aaa * bbb = a³b³

^bLog(x)=y <=> b^y=x

Rule 1:

^glog(a) + ^glog(b) = ^glog(ab)

Rule 2:

^glog(a) - ^glog(b) = ^glog(a/b)

Rule 3:

n * ^glog(a) = ^glog(aⁿ)

a^f(x) = a^g(x) => f(x) = g(x) (usually an ordinary equation).