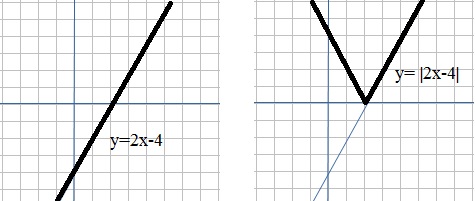This note is especially for beginners.

Maybe you need to pick up "some" basic "mathematics" rather quickly.
So really..., my emphasis is on "rather quickly".

So, I am not sure of it, but I hope that this note can be of use.
Ofcourse, I hope you like my "style" and try the note anyway.

Contents:

1. Absolute value functions.
2. Functions with a parameter.
3. A few words on eliminating a variable in solving equations.

1. Absolute value functions.

This means that we now have the requirement that "y", or f(x), is ≥ 0.
So, if you would sketch the function in the coordinate system, it may only have positive values for "y".
In effect, the function is always above the x-axis, or may touch it in which case f(x) is "0".
We denote the "Absolute value function" by |f(x)| where f(x) is some continuous function which may have
positive and negative values. For the domains where f(x) is negative, then simply mirror the graph
in the x-axis, in order to get |f(x)|.

Example 1:

Suppose we have the line y=2x-4.

It's not hard to sketch this function.
- If y=0, we have the intersection with the x-axis. So, 2x-4=0 => 2x=4 => x=2.
- If x=0, we have the intersection with the y-axis. So, y=2*0 - 4 => y=-4.
- You can also see "the slope" of that line, which is "2".

In this case, the "absolute value function" would be written as f(x) = |2x-4|.



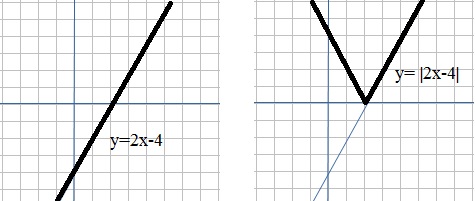
You could just look at y=2x-4, and for those values of "x", where the function goes negative,
then "mirror" that part in the x-axis, to get y=|2x-4|.
With a little pondering, you would agree, that for the negative part, we simply can multiply
that with "-1", which is in effect, mirroring along the x-axis.

Now, most important is to be able to write down the correct function regulation for |2x-4|.
Here it is:

Since this fuction gets positive as of x=2, we can write:

                2x-4 when x ≥ 2
|2x-4| = {
                -(2x-4) = -2x +4 when x < 2

Example 2:

Let's consider f(x) = | x² - 4x|. Give the function regulation for this absolute value function.

f(x) = x² - 4x is a regulr parabola, with it's "nose" pointing downwards.
It's useful to see for which "x", this function gets negative.
For this, finding the intersection(s) of the parabola with the x-axis, is helpful.
If we have those, we cn simply determine the intervals where the function is positive
or negative.

x² - 4x = 0 => x(x-4) = 0 => x=0 or x=4.

You may sketch the function, ofcourse, but in fact we already have the neccessary information:

                    x² - 4x when x ≥ 4 and x ≤ 0
|x² - 4x| = {
                    -(x² - 4x) = -x² + 4x when 0< x < 4

Take good care in deriving the negative -(f(x) of a function:
Suppose you need the negative of "x²-4x", then it will become -(x²-4x) = -x²+4x.

What's in red above, is exactly the heart of the matter. It's important to be able to accurately
write down the intervals for which the function |f(x)| must be expressed in component functions.

2. Functions with a parameter.

Here we mean functions y=f(x), with an additional parameter"p", which can be any number, like in
for example:

y=3x + 1 + 2p
y=x² + 2x + p
y=x² + 4px + 16

Now, if you have a certain "p" (like p is 2, -3 etc..), then you end up with an ordinary and well-known equation.

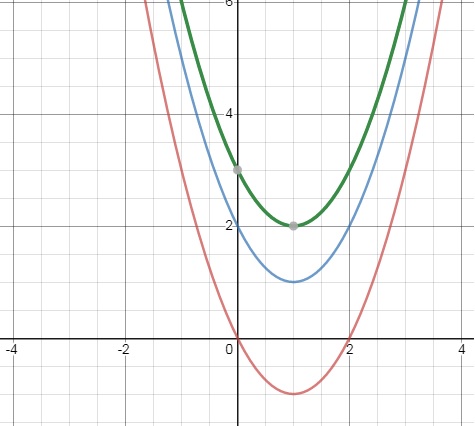
Suppose you take a look at y=x² - 2x + p

If p=0, then y=x² - 2x
If p=1, then y=x² - 2x + 1
If p=2, then y=x² - 2x + 2
etc..
In such a case, a family of parabola exists, which only differ in a "translation" of "p", of f(x),
in the y direction. See the figure below for a few examples, where p=0, p=2, and p=3.
This is already what we knew from note 3, that in the general equation y=ax²+bx+c,
that "c" is just merely an upward (c is positive) or downward (c is negative) translation.



So, what can you expect on an exam, or other test?

-Well, for example, for which values of p, does (for example) y=x² - 2x + p have
0, 1, or 2 intersections with the x-axis. Then we must take look at the "Discrimant" (see note 3)
to investigate that. The "Discrimant" then will have "p" in it's expression.
-As another example, for which value of p will (for example) y=x² - 2x + p pass through
a specific point (a,b), where that point is exactly defined, like (4,8).
etc... etc...

Example 1:

For which p, does y=x² -6x + p=0, has two solutions?

For two solutions, the Discriminant must be greater than 0, or D >0. Thus:

(-6)² - 4*1*p > 0 =>
36 - 4p > 0 =>
-4p > -36 =>
p < 9

So, for the equation x² -6x + p=0, to have two solutions (intersections with the x-axis),
then for the parameter p, it must hold that p < 9.

Example 2:

Suppose we have the function f_p(x)=p + √(x-p).
In this example, there is no need to exactly calculate the solution in (5).
It's sufficient if you would understand the "reasoning" behind the answer.

(1). Explain why for f₁, x≥1.
(2). Explain why for f₂, x≥2.
(3). Scetch f₁, f₂ and f₃.
(4). Explain why, in general, we must have p≥1.

(5). Proof that g(x)=x+¼ is tangent to all f_p.

First, calculate f'(x):

f'(x) =

d/dx (p + (x-p)½)

=

1 -------- 2 √(x-p)

If g(x)=x+¼ is tangent, then for those x values must hold that f'(x)=1,
since the equation of the tangent line is g(x)=x+¼.

Thus:

1 -------- 2 √(x-p)

= 1

=> x=¼+p

Substitute this into the equation of f_p, will show the validity of the statement.

Example 3:

Suppose we have the function f_p(x) = x² + px.

As usual, this defines a collection of functions, each with it's own value of "p".

(1). Write down the general solution(s) for the intersection with the x-axis.

x² + px = 0 => x(x+p) = 0 => x=0 or x= -p

(2). Determine which f_p(x) passes through the point (1,3).

Simply substituting (1,3) into f_p(x) gives:
1² + p = 3 => p=2.

Thus f(x) = x² + 2x goes through the point (1,3).

Example 4:

Take a look at the family of functions f_p(x) below:

fp(x)

=

5 -

p --- x2

For which p, will have f_p(x) intersections with the x-axis?

We will analyze this function, without shuffling with equations.

- First note, that "x" may not be "0", so we should see asymptotic behaviour with respect
to the y-axis.

-Note the second term p/x² more closely:

No matter what p is, if x get's very large, this second term goes to zero.
Also, no matter what p is, if x get's very small (as a negative number), the second term
goes to zero too.
Thus it looks like that y=5 is an asymptote too.

If the number "5" was replaced by another number, like "n", the same effect will be true,
and this time y=n would be the asymptote.

Now, if x approaches "0", then:

If p is a postive number, then p/x² will approach +infinity.
If p is a negative number, then p/x² will approach -infinity.

All in all, you may conclude that intersections with the x-axis exists, if p<0.

Example 5:

Suppose we have f_p(x)=3x²+12x+p.
For which "p", does f_p(x) has an extreme value of "8"?

Here we mean the value of "f(x)" for which this maximum or minimum value of y is met.
Since this is a parabola with it's nose down, so it must be a minimum.

As you have seen in note 3, the corresponding extreme value (x_extreme) is found by -b/2a,
using the general expression of f(x) = a x² + bx + c.

So here we must have: x_extreme = -12/2*3 = -2.

For that x value, we have:

f_extreme = 3*(-2)² + 12*-2 +p = 8.
=>
12-24+p = 8 => p=20.

3. A few words on eliminating a variable in solving equations.

You did already performed this in various situations.
In this section, I will make it a bit mor explicit.

-free lunch elimination:

Just imagine some parabola, and some line. That line may cross the graph of the parabola
at two points, or just one, or maybe not at all. It just depends on the slope of that line, for example.

How can we find the coordinates of the intersections?

Suppose the parabola is denoted by f(x).
Suppose the line is denoted by g(x).

If they intersect, then at those two points (or just that one point), f(x) must be equal to g(x).

Let's try an example:

Suppose we have:

f(x)=2x² -3x + 2
g(x)=3x + 2

Find the point(s) where they intersect (if any, ofcourse).

In order to find the "y" values, we do this:
At the intersections, f(x) must be equal to g(x), so we must have "y=y":

2x² -3x + 2 = 3x + 2

We are going to solve that equation. Bring "3x" to the left, and "2" to the left:

2x² - 6x = 0 =>

x² - 3x = 0 =>

x(x-3) = 0 =>

x=0 and x=3

Those "x's" can be put in either of equations above, to find the corresponding "y's",
which gives us the points (x,y) where the graphs intersect.

If you look above, we immediately (sort of) eliminated y, because where the functions intersect,
f(x)=g(x), meaning th y values are the same at the intersection(s), so we ended up
having one equation with "x's" only.
A sort free lunch elimination...

-System of equations:

Here we may have two linear equations (or one, or both, is quadratic).

Let's say we have two linear equations. Again, one interpretation is, that we try to find
the intersection of those lines, when we try to solve that system of equations.
In note 2, you can find all about finding intersections. But, this time we will use
a slightly different method.

First this: you might be used to the "y=ax+b" notation, to describe lines.
But it's easy to rewrite any such equation to the "mx+ny=c" notation. Just look at this example:
Suppose we have an equation in the traditional format:

y = 2x + 3

Then how to rewrite that to the other format?
It's really easy. On both sides of the "=" symbol, we may add or subtract any number, or term,
and it makes not difference. As long as we do it at both sides.
You may even multiply all terms on both sides of the "=" symbol, with the same number.

So, if we add -2x to both sides, we have:

-2x + y = 2x + 3 -2x

And that will resolve to:

-2x + y = 3.

Now let's take a look at an example of the new method, to solve a set of equations.

Again, one interpretation can be that you want to find the intersection (if it exists)
of two lines. Note that we are dealing with linear equations (but another type of reasoning
applies to higher order functions as well).

Suppose we have the following two linear equations:

3x + y = - 3
x + 2y = 1

We want to eliminate either x or y, and we are looking for a suitable approach.

For any equation it is true, that you may multiply both sides of "=", with the same number,
or divide by the same number, or add/subtract both sides with the same number, as long as
as you do it on both sides.

So, for example "2*8=16" is equal to 2*(2*8) = 2*16. It works the same for division etc..

Let's multiply the first equation with 2, giving:

6x + 2y = - 6
x + 2y = -1

We can eliminate "y" by subtracting the second equation from the first.
It sounds like a trick, but it's essentially another way of rewriting "substituting"

6x + 2y = - 6
x + 2y = -1
-----------
5x = -5

So, 5x=-5 => x=-1.

For finding "y", you can use any of the two original equations. Let's use the first one.

6 * -1 + 2y = -6 => 2y =0 => y=0.

Let's verify using the second one:

-1 + 2y = -1 => y=0.

So, the intersection of those lines is the point (-1,0).

For this method, just multiply or divide one equation with a suitable number,
in order to add or subtract both each equitions, so that you can eliminate "x" or "y".

-Example elimination of a variable with vector notation of lines:

If you are not so comfortble with vector representations of lines, then you can easily
skip this section.

In this section, we can see another example of how to get rid of one variable
in a set of equations. This time, we will use a vector representation of a line in R².

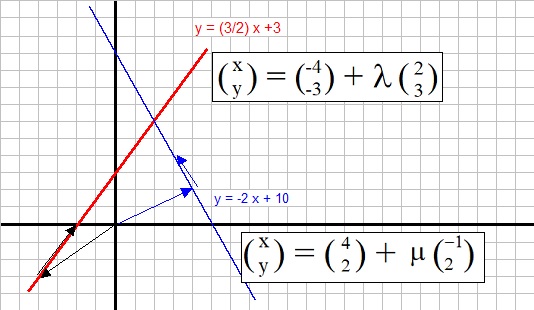
Suppose we want to find the point of intersection of the two lines:

y = 3/2 x + 3
y = -2x + 10

Obviously, where the lines intersect, the "y" (and "x") of both lines are the same.
So, we must solve:

3/2 x + 3 = -2x + 10 =>

3x + 6 = -4x + 20 =>

7x = 14 =>

x = 2.

We can find the corresponding "y" by using either one of the equations, and substitute "x=2".
Then we will find "y=6". So the point where both lines intersect is (2,6).
We have seen this theory before in "note 2: Linear Equations".

Now, we will do the same, but this time with the vector representations:
In the figure below, you can see both lines as described above, along with their
vector representations.

┌ x ┐ └ y ┘

=

┌ -4 ┐ └ -3 ┘

+

λ

┌ 2 ┐ └ 3 ┘

┌ x ┐ └ y ┘

=

┌ 4 ┐ └ 2 ┘

+

μ

┌ -1┐ └ 2 ┘

At the intersection, the "x" and "y" at that point must be the same for both lines.
Thus we have:

-4 + 2λ = 4 - μ   (equation 1)
-3 + 3λ = 2 + 2μ   (equation 2)

This is a set of two equations with two variables. We can solve it in the following way:
I want to isolate either λ or μ. I can do it like so: Multiply equation 1 by "2", and then add both equations:

-8 + 4λ = 8 - 2μ
-3 + 3λ = 2 + 2μ
---------------------------
-11 + 7λ = 10

-11 + 7λ = 10 =>

λ = 3.

Now, I may use the vector equation:

┌ x ┐ └ y ┘

=

┌ -4 ┐ └ -3 ┘

+

3 *

┌ 2 ┐ └ 3 ┘

=

┌ -4 ┐ └ -3 ┘

+

┌ 6 ┐ └ 9 ┘

=

┌ 2 ┐ └ 6 ┘

This is indeed the vector (from Origin) pointing to (2,6). So, we have found the point of intersection
of both lines. Note that the traditional representation (2,6), and the "vector", are equivalent in this context.

That's it. Hope you liked it.