In the series: Note 4.
Subject: the Sine and Cosine functions (NL/Dutch: Sinus en Cosinus functions)
Date : 23 Februari, 2016Version: 0.3
By: Albert van der Sel
Doc. Number: Note 4.
For who: for beginners.
Remark: Please refresh the page to see any updates.
Status: Ready.
This note is especially for beginners.
Maybe you need to pick up "some" basic "mathematics" rather quickly.
So really..., my emphasis is on "rather quickly".
So, I am really not sure of it, but I hope that this note can be of use.
Ofcourse, I hope you like my "style" and try the note anyway.
This note: Note 4: The Sine and Cosine functions.
Each note in this series, is build "on top" of the preceding ones. If you are not familiar with, for example,
"linear equations" in the form of "y=ax+b", then it's highly recommended to read Note 2 first.
If you are not familiar with, quadratic equations" in the form of "y=ax2 + bx + c",
then it's highly recommended to read Note 3 first.
In fact I am sure that this note "works", if you are at least at the level represented by notes 2 and 3.
1. Introduction.
When you come "into touch" with mathematics, there is no way to escape "linear equations", "quadratic equations",and some important "trigonometric functions" like the "sin(x)" and "cos(x)" functions.
Yes, we are going to explain those functions here, so that you are able to use them, and understand the theory.
The sine (wave) "function" is often visible in natural events. For example, electromagnetic radiation (e.g. radio)
exibits a "wave-like" nature, which can be expressed mathematically as sine functions.
Also much closer to home, you can see 'sine-like' phenomena, like AC electrical signals, or waves in all sorts of media,
or making of pure musical notes with instruments, the vibration of snares etc.. etc..
When "something" vibrates, it does that with a certain frequency. The periodic swing of a common pendulum,
can also be expressed by a sine function.
There are many excellent pictures and animations on the Internet, but they are not always free and in the public domain.
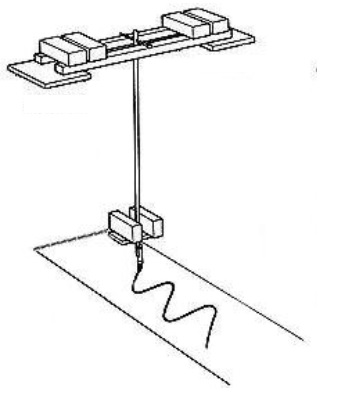
However, the simple picture in figure 1 is. And it will do nicely.
Suppose you have a pendulum. At the bottom end, you attach a pen, or pin, of some sort. This pin, can draw
a line on a sheet of paper. This paper moves in a uniform (constant) speed.
Suppose that the pendulum was at rest first. Next, you displace it sideways from its resting position, and
let it go. It will start swinging from one side to the other opposite site.
Now, what is drawn on the paper, is a great example of a sine function.
As you know from experience, at the lowest point, the pendulum has it's maximum speed. Then, when it start to climb,
it's velocity decreases, until it reaches it's maximum displacement where the speed is "0", and then the motion is reversed.
Figure 1.
The animation in figure 2 is instructive too. Here you see a uniform circular motion. The object in "orbit"
moves with a constant velocity around the center of a circle.
Note that there is another point too, moving along the vertical axis.
That point is the projection of the object in "orbit", along the vertical axis, and note how it exactly
mimics the movement of a pendulum.
Figure 2.
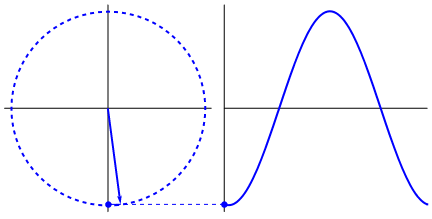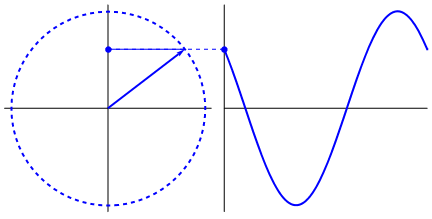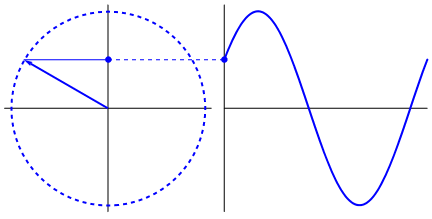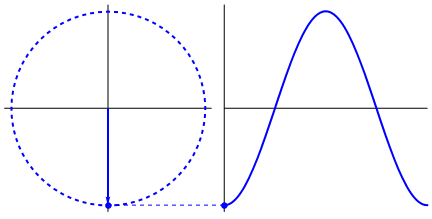
Source: https://commons.wikimedia.org/wiki/File:Sinus-visualisation.gif
For the point occilating on the vertical axis: if we would mount a pin on it, and we let a sheet of paper
move to the right (with a uniform speed), we would get a sine wave on paper again.
Here is an example of a sine function, plotted in the (usual) XY coordinate system.
Figure 3. An example of a sin function.
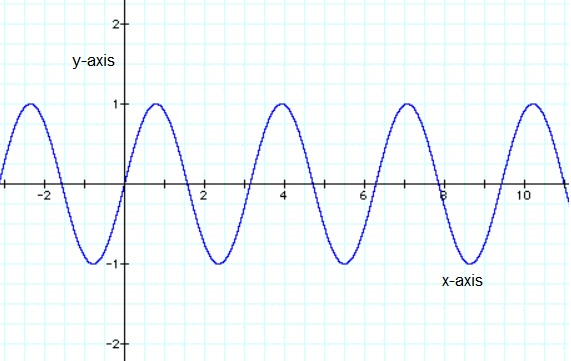
If the pendulum was swinging much faster, the peaks and crests were much closer together. On the other hand,
if the frequency was much lower, there was more distance between the peaks and crests.
In the preceding notes on linear equations (lines) and quadratic equations (parabola), we were used to
plot the functions in the (usual) XY coordinate system.
However, one might also say that the "displacement" (d) of the pendulum with respect to the center (when it's in rest),
should be plotted against "time" (t).
Look again at figure 1. As the paper moves (and the pedulum moves), the paper "registers" the position of the
pendulum with respect to time. The figure on the paper really tells us, where the pendulum was, at a certain time.
So that's why, for example physicists, replace the "y" of the "y-axis" with "displacement" (or amplitude),
and the "x" of the "x-axis" with "t" of time.
That's not really fundamentally different. Once upon a time, mathematicians choose the represent the axes by "y" and "x",
but it could also have been, in a manner of speaking, by the "v" and "w" axes. There is no fundamental difference here.
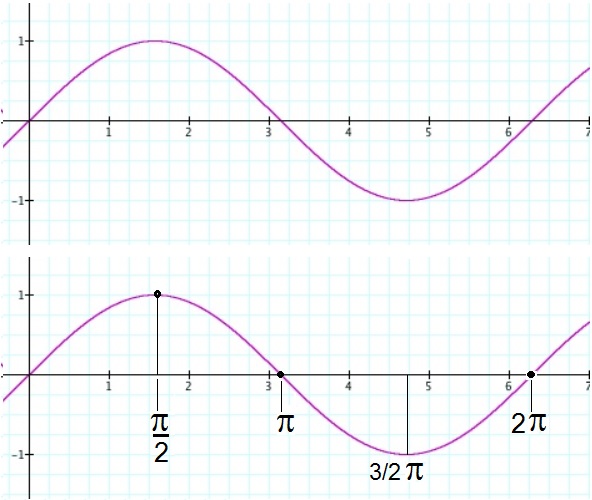
The figure below shows us the y=sin(x) function, where x is a socalled "Real" number, but plotted are
the usual integers as 1,2,3 etc..
However, when talking about sin() and cos() functions, the number "π" plays a very important role.
The two figures below, are equivalent. But, in the lower figure, I explicitly showed "π" as well.
The number "π" will be explained in section 2.
Figure 4. y=sin(x).
2. Functions of an angle, and what's π anyway?.
2.1 The mystery of π
The circumference of any circle, has been found to be "2 x π x r", (where r is the radius),which we simply will write as "2πr" (leaving out the multiplication symbol).
Note that if "r" is the radius, then "2r" is the diameter of a circle.
It's not so strange, that the circumference is related to r, since, if the radius "r" would increase,
then so would the circumference. If r is decreased, then so is the circumference.
However, although the "formula" 2πr is not really complicated, it sure is not easy to proof!
The number "π" has puzzled lots of people (at least as early as 1600 BC). It was indeed found, a long time ago,
that the ratio of "circumference : diameter" was constant, no matter what length of r was chosen.
That is: "circumference : diameter" = 2πr / 2r = π
All sorts of nifty approximation methods were used, and it was found that the value
of π is very close to 3.14, but that's only an approximation.
As an example: suppose you need to calculate the circumference of a circle which has a radius of 2 meters,
then the circumference = 2 x 3.14 x 2 = 6.28 x 2 = 12.56 m.
In many cases, like the simple example above, the approximation of "3.14" is good enough.
However, we must keep in mind that for many scientific- and enginering implementations,
a higher precision is required.
Although you cannot say that it is really "mysterious", the decimal representation of the fraction ".14" in "3.14...",
actually never ends, and you can try to be more and more precise, without end.
Today, high-end supercomputers have calculated the value of "pi" to many, many, thousends of digits (behind the "dot", or "comma").
As a sidenote:
Although a circle (or sphere) is a common object, it really stands out in having "complete symmetry".
Do you know of any other geometrical object, where you can draw a line through any point of the circumference,
and the center, which will always splits it in two equal parts?
2.2 "Formal" definitions of the sine and cosine
We have seen that a sine function emerges "naturally" from the oscillation of a pendulum.For all socalled "harmonic oscillators", which vibrate or move with a fixed periodicy (frequency), we can say
that they can be described by a sine (or cosine function), or a "sum" of such functions.
By the way, in a moment we will see that the sine and cosine are actually equal, except for a phase difference.
What ever that is (the phase difference), we will learn about that in a moment too.
However, first we need to review a (sort of) "formal definition of the sine and cosine functions.
Figure 5.
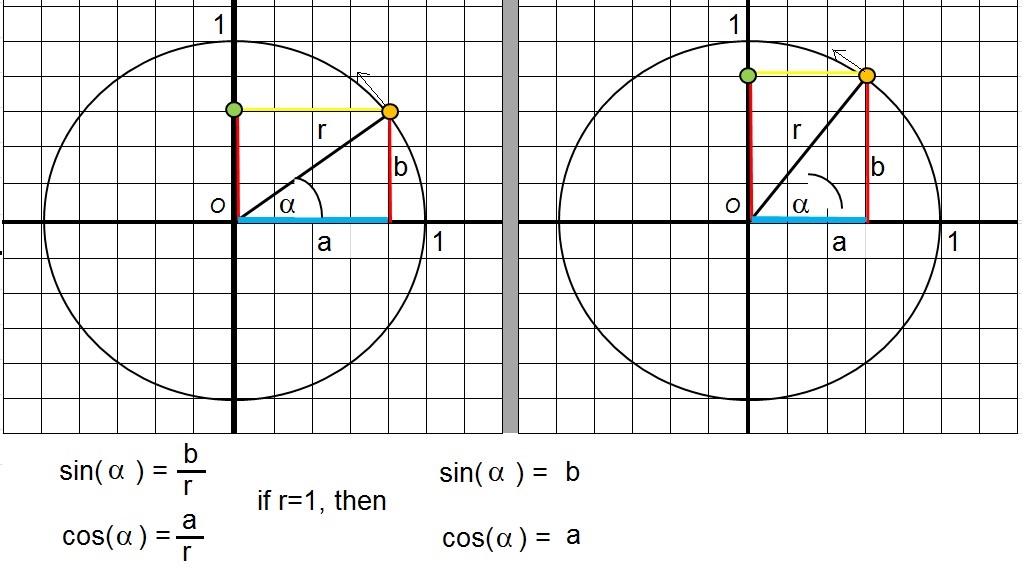
In the figure above, you a circle on the left side, with radius "r". When you "project" r on the x-axis,
you get the blue piece of line (along the x-axis). Let's call that piece of line "a".
When you "project" r on the y-axis, you get the red piece of line, but this time shown on the right.
Let's call that piece of line "b".
Note that we have right-angled triangle, enclosed by "r", "a" and "b".
Note also that we have an angle, let's call it "α", between "r" and "a".
In the figure above, we see the formal definitions of sin(α) and cos(α):
| sin(α)= | b - r |
| cos(α)= | a - r |
Note that "an angle keeps the same value", no matter how much we "inflate" the triangle.
So, even if all the sides are 10 times as long, the only thing that matters is the relative ratio
between the sides.
For example: sin(α) = b/r = 10b/10r = 99b/99r = 0.2b/ 0.2r etc.. etc...
Now, if r=1, then we get very simple formula's:
sin(α) = b
cos(α) = a
If you say: "I still don't see the connection with the sine graph examples...", then I don't blame you.
But here it comes:
In the circle, on the y-axis, you might note the "green" dot. Just picture the green dot in motion, just
as we have shown in figure 2.
That is, the green dot mimics the pendulum movement, en swings along the y-axis, up and down, just as a pendulum would do.
Actually, as we saw in figure 2, it's the orange dot which moves along the circle with a uniform speed.
This makes the projection (the green dot) "act" like a pendulum.
Now, attention please!
Every time the green dot (or orange dot) changes position, then the length of a or b changes too.
Let's focus on "b" for a moment. When the green dot is in the Origin then b=0. But as the green dot moves up,
b get's longer, or in other words "sin(α)" get larger, all the way up to "1", when the green dot has
it's maximum. Then the green dot starts moving downwards, en b=sin(α) get smaller.
When the green dot is in the Origin again, b=0. But the green dot keeps decending, meaning that b get's a negative value,
all the way "down" to "-1". Then, the green dot starts moving up again etc.. etc..
Now, please take a look again at figure 4 (and you may ignore the values on the x-axis for a moment).
Would't you agree that the value of the length of "b", is reflected in the curve, as time passes, "moving"
from the value "0" to "+1" then moving to "0" again, all the way down to "-1", and then starts "to climb" again etc.. etc..
Since sin(α) = b (if r=1), we also may say that we have a curve (or function) notated by "sin(α)".
But what do have on the x-axis on such a curve? Angles?. Yes that is true, so we have for example 30 degrees, 90 degrees etc..
However, mathematically, we often have the numbers 1,2,3 etc.. on the x-axis. So is that a conflict?
No, you may list a (continuus) range of angles on the x-axis, from 0 degrees to 360 degrees.
Or, you may use the usual numbers. However, that does not look "very nice", but it is still correct.
This is why people often arrange fractions of "π" along the x-axis, as is shown in figure 4, the lower figure.
In a moment, more on this.
Now what about "a"? Above, we have seen the story of "b". Indeed for "a", a similar story holds.
This time, you need to imaging a "green dot" going continuously from left to right.
However, there is a small "phase difference" between both stories.
If the green dot is in the Origin, then b=0, but a is at it's maximum, namely "1". This is so since "r"
lies completely along the x-axis, and thus the blue line segment "a" coincides with "r".
Then, suppose the the green dot moves upwards, making "a" smaller. When the green dot is at it's maximum,
then "a" is 0 (while b=1).
etc.. etc..
Since a=cos(α), the sine and cosine functions are identical, but the cosine is a small phase "ahead"
compared to the sine function.
It's very instructive to see the (standard) sine and cosine curves, in one figure:
Figure 6. sin(x) and cos(x)
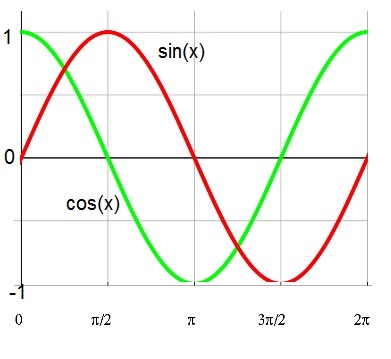
I still have to explain the values along the x-axis.
Since we started by using the sine of an "angle", like "sin(α)", you may ofcourse divide the x-axis in degrees (from 0 to 360).
You may also divide the x-axis using the ordinary numbers like 1, 2, 3 etc..
But where is the "match"? This will be explained in section 2.3.
Note that figure 6, shows us just one period of both the sine and cosine functions.
Since the pendulum keeps swinging (if we ignore all frictions), then the sine and cosine functions
will repeat the "period" over and over again.
2.3 Radians
Suppose the circle in figure 5, has a radius of r=1. Now suppose the orange dot is on the x-axis, and movesupward, counterclock wise. Ofcourse, that dot follows the circle. There comes a brief moment, where the "arc"
on the circle, has a length of 1 too (equal to "r"). Only for a smart moment ofcourse, since the orange dot is in motion and the
length of the arc increases continuously.
It's really quite special when the arc-length is 1 too, and thus (at that moment, equal to "r")
It happes when α is about 57.3 degrees.
The remarkable thing is, is that if we perform "π x 57.3 = 3.14 x 57.3" we get 180 degrees.
(remember, &960; is about 3.14).
Expressed in such way, by agreement, people often say that at 180 degrees, we are at π radians (rad).
This is one reason why people also often say:
If we start from the point (1,0) on the x-axis, and:
- we rotate 90 degrees counterclock wise, we are at 90 degrees or π/2 (or π/2 rad) .
- we rotate 180 degrees counterclock wise, we are at 180 degrees or π (or π rad).
- we rotate 270 degrees counterclock wise, we are at 270 degrees or 3/2π (or 3/2 π rad).
- we rotate 360 degrees counterclock wise, we are at 360 degrees (or 0 degrees) or 2π (or 2π rad).
If you are going to do a lot of math with trigonometric functions, it's probably a good thing to remember
the following table:
| degrees: | π rad: |
| 45 | π/4 |
| 60 | π/3 |
| 90 | π/2 |
| 180 | π |
| 270 | 3π/2 |
| 360 | 2π |
Let's now plot the standard sine function, using a few numbers, degrees, radians on the x-axis.
Figure 7. Different scales on the x-axis (numbers, degrees, radians)
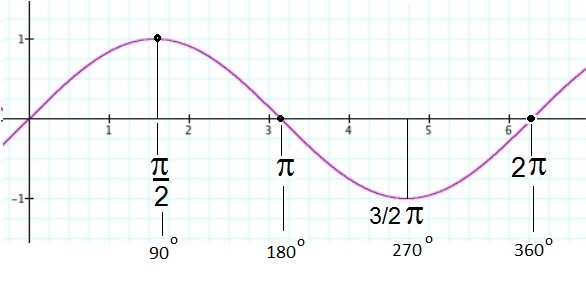
In figure 7, we have three different "representations" of the possible "x-values": numbers, degrees, radians.
- Sure, you might use "common" numbers on the x-axis, like (1,2,3,5, etc..), but since π is 3.14, you might as well
put in π/2, π, 3/2 π, and 2π too. We also know that these corrspond to 90, 180, 270, and 360 degrees (in that order).
- Sure, you might use degrees on the x-axis, from 0 to 360 for one Period. But then you might as well
put in π/2, π, 3/2 π, and 2π too. We know that these simply corrspond to 90, 180, 270, and 360 degrees (in that order).
2.4 The Tangent:
As the last "standard" "trigonometric function", we will introduce the "tangent()" function here.I am sure that it will amaze you, how completely different it "looks", compared to the "nice" periodic sine and cosine functions.
Just as we did with the sin() and cos(), let's collect all formal definitions here:
Please remeber that the definitions refer to a right-angled triangle, enclosed by "r", "a" and "b".
Otherwise, if needed, please take a look at figure 5. again.
Here are the definitions:
| sin(α)= | b - r |
| cos(α)= | a - r |
| tan(α)= | sin(α) ---- cos(α) |
Or, we can also write that as: tan(α) = sin(α) / cos(α) = b / a
Looking at the moving orange dot (in figure 5), moving counterclock wise along the circle, we know that the sides "a" and "b",
both vary between -1 and +1. If "b" = 0, then simply tan(α)=0. However, if "a" gets nearer and nearer to 0, then
tan(α) tends to diverge to an infinite high value.
The figure below shows you the standard tangent function. Note how it diverges (goes to infinity) in the close vincinity
of various points.
Figure 8. Standard tangent function.
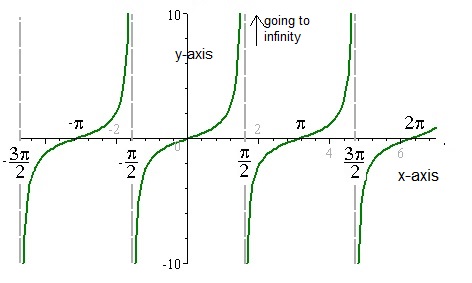
Note that, for example if x=π then sin(π) is "0" and thus tan(π) is "0".
However, if x=1/2 π, then cos(1/2 π) = "0", meaning that tan(1/2 π) is "not defined", meaning going to infinity.
3. The sine function (or cosine) with other "frequencies".
What would we see if we investigate functions like f(x)=sin(2x), or f(x)=sin(3x), or in general, f(x)=sin(nx)?I will make it plausible, that if "n" increases, the function will "oscillate" faster.
Figure 4 shows you the standard f(x)=sin(x) function. For x=π, then f(x)=sin(π)=0.
You can also check that with figure 4.
Now, suppose we have the function g(x)=sin(2x). Now, already for x= 1/2 π, then g(x)=sin(2 * 1/2 π)=sin(π)=0.
So, already for "x is half pi", we have that g(x) is "0". It seems that g(x) ocillates twice as fast as the standard sin(x).
This will be explained more thourougly in the "task" below.
Now take a look at figure 10. Here we see the functions sin(2x), sin(3x), and sin(4x) compared to sin(x).
Figure 10. The sin() function with different "frequencies".
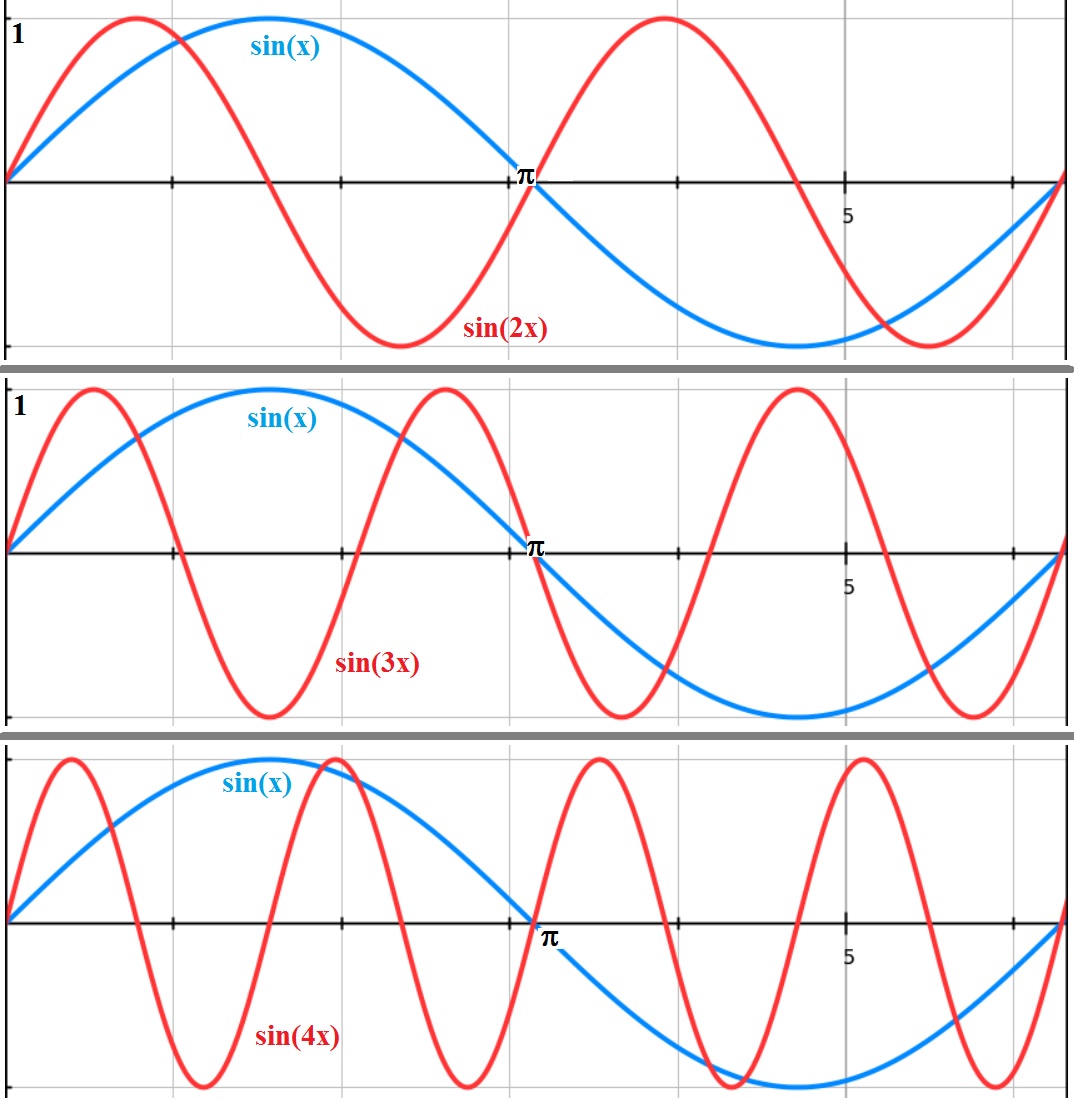
How fast a sin(nx) function ocillates, is expressed in how many "periods" fit in the interval [0,π].
The "more" periods fit, it also said that the higher it's "frequency" is.
The following excercise will explain this better:
Task: plot the function y = 3 sin(2x)
Solution:
Maybe this task looks difficult at first sight.
No, it's really quite easy. First, I am not going to plot anything here.
I will only use a small bit of logic.
I say that "sin(2x)" is simply 2x denser in peaks and crests, compared to the standard "sin(x)".
You know, for example from figure 4, that sin(x) has it's first peak at π/2, and it's first crest at π.
Now look what happens:
For sin(2x) those first peaks and crests are happening much "earlier". Look at sin (2 x π/4) = sin(π/2).
That means, if we try π/4 for "sin(2x)", we get the same as sin(π/2).
So, sin(2x) gets it's first peak already at "π/4", compared to sin(x) which has it's first peak at π/2.
Similar reasoning holds for the other peaks and crests.
In a way you may say that sin(2x) oscillates twice as fast as sin(x). So, two full periods of sin(2x),
will fit in one period of sin(x).
So, what would happen with sin(3x)? Then 3 periods of sin(3x) will fit in one period of sin(x).
Thus, if you would look at sin(n x), where n is a whole integer, the larger n is, the faster the function "ocillates".
And "n" periods of sin(n x) will fit in the period of the standard sin(x).
It's completely the other way around if "n" would be a fraction.
If we would have a "fraction", that is something like sin(1/2 x), or sin(1/3 x), then those functions
are more "stretched" compared to the standard "sin(x)" function.
For example, 3 standard "sin(x)" periods, will fit into one period of "sin(1/3 x).
Now what about the "3" in "y = 3 sin(2x)"?
Just as with any other function, this has only an effect on the "amplitude" or values of y.
It does not have an effect on the rate of oscillations (or periods).
For example, sin(x) (or sin(2x) for that matter), has a maximum value of "y=1", for some values of x.
The "3" in "y = 3 sin(2x)", simply means we multiply every "y" with 3.
So the max value of "y = 3 sin(2x)" is "3" (instead of "1").
In the end, it's very simple to determine how a function like "y = A sin(Bx)" would generally look like.
4. Examples.
Example 1.
Suppose we have a right-angled triangle, enclosed by "r", "a" and "b", just like in figure 5.Suppose further that:
r = 2
a = 1.73
b = 1
The angle α between the side r and a is 30 degrees
Task: Calculate sin(α) and cos(α).
Solution:
sin(α)= b/r = 1/2 = 0.5
cos(α)= a/r = 1.73/2 = 0.87
Ofcourse, if you have a calculator, you could have typed in sin(30) and cos(30), and obtained the result immediately.
Also, if you have accurate graphs of the sine- and cosine curves, then you could have read the results from
the graphs, by finding the "y-values" at x=30 degrees.
Example 2.
Suppose we have a right-angled triangle, enclosed by "r", "a" and "b", just like in figure 5.Suppose further that:
r = 5
a = 3
b = 4
Task: Calculate sin(α) and cos(α). Also, determine the angle α between r and a.
Solution:
At this point, we do not know angle α, but we sure can calculate sin(α) and cos(α),
since we know the values of a, b, and r.
So:
sin(α)= b/r = 4/5 = 0.8
cos(α)= a/r = 3/5 = 0.6
Ok, we have the sine and cosine values. To get the angle, we could use the sin-1(0.8) function which is
the inverse of the sine function. But, we have not seen those inverse functions yet.
So, we are not going to use that method, yet. So, what now?
Having a accurate graph of the sine function, then where y=sin(x)=0.8, we find an angle of about 54 degrees.
Or, there also exists tables which lists the sin, cosine, tangent, for every single degree from 0 to 360.
Is that old-fashioned? Absolutely, but it works.
Example 3.
This is a nice one. If one side of a right-angled triangle is unknown, like for example "a",but we know the angle between "a" and "r", the we can calculate "a" from the cosine of the angle.
Here is an example:
See figure 9. Suppose we know "r", "b", and the angle. But not "a". Can we still derive it?
Figure 9. Standard tangent function.
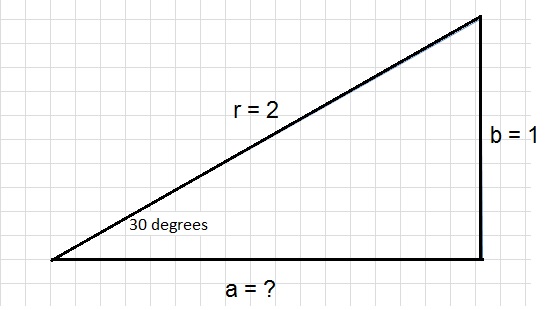
So, suppose:
r = 2
a = unknown
b = 1
The angle α between the side r and a, is 30 degrees. We need to find "a".
Solution:
We know (or we can calculate) that cos(30)= 0.87. Thus:
cos(30) = 0.87 = a/r = a/2
Thus a = 2 x 0.87 = 1.74
So we have found the length of side "a", since we knew "r" and the angle between "r" and "a".
Note:
You might also say: I just use "Pythagorean theorem" here. Yes, that works too.
If you know the lenght of 2 sides of a right-angled triangle, you can always calculate the unknown one.
So, a2 + b2 = r2 => a2 = r2 - b2
Filling the values of "r" and "b":
a2 = 4 - 1 = 3 => a = √3 = 1.74
5. Quickly determine the shape, frequency, amplitude from the formula.
In general, we may hve the functions:f(x)= y= a + bsin(vx-w) (a,b,v,w are some constants)
f(x)= y = a + bcos(vx-w)
We can view those, in a different format:
f(x)=y=a + bsin(c(x-d))
f(x)=y=a + bcos(c(x-d))
Both latter equations may seem a bit particular, since you might expect a general relation to be
in the form like f(x)=y=a + bsin(cx-d).
The reason for that will become clear in a moment.
You can interpret the a,b,c, and d, rather quickly, to quickly get an idea "on how the function goes".
(1). The "a" means a "shift" up or down along the y-axis, depending on the sign of the number "a".
This is so, since you simply add a number "a" to f(x)=sin(x) or f(x)=cos(x).
So, if you for example add "2" to f(x)=sin(x), it will become f(x)=sin(x) + 2,
meaning that the graph is lifted "2" in the plus direction of the y-axis.
(2). The "b" is related on how high the "amplitude" of the function is. If you, for example,
multiply f(x)=sin(x) with "2", then we have f(x)=2sin(x), making the peaks and crests of sin(2x)
2 times as large, compared to sin(x). Likewise, if we have f(x)=1/3 sin(x), that will lower the highs and lows of sin(x),
to be 1/3 compared to the basic function f(x)=sin(x).
(3). The "number" c (in cx), relates to the frequency of the sin or cos function.
As already demonstrated in the text above, the function sin(3x) oscillates 3x faster compared
to the basic function sin(x). Likewise, the function sin(1/2x) oscillates 2 times slower compared
to the basic function sin(x).
Instead of "frequency", we can also use the term "period" (meaning one full cycle).
So, sin(3x) has a shorter period compared to the basic function sin(x). Indeed, 3 full cycles
of sin(3x), "fit" in one full cycle of the basic function sin(x).
(4). Now, a small trick, explaining why I wrote (c(x-d)):
If you want the starting point of the first full cycle near the Origin, then we have:
f(x)=y=a + bsin(c(x-d)): point (d,a)
f(x)=y=a + bcos(c(x-d)): point (d,a+b)
So, if you want to take advantage of that, then rearrange the terms inside the brackets a bit
to be in the form "(c(x-d))".
So if you have the function f(x) = -2 +3sin(3x-π), then write it as f(x)=-2 +3sin(3(x-1/3π))
6. The Inverse functions.
Suppose we have f(x)=y. Now, in many cases (but not all), there exists an "inverse" function "g", in such a waythat g(y)=x, or in other words, g(f(x)=x, which returns "x" again.
So, first we apply f to "x", then g on f(x), returning "x" again.
The inverse function "g" is often denoted as f-1, so:
f-1 (f(x) ) = f (f-1(x) ) = x
A simple example is f(x)=x2 and g(x)=√x (for the domain x>0).Indeed g(f(x))=√(x2)=x.
The sin(x), cos(x), and tan(x), have inverse functions too, often denoted by sin-1(x), cos-1(x), and tan-1(x).
But you may also encounter the names arcsin, arccos, and arctan.
The inverse functions have limited domains (part of the x-axis) for which they are valid.
The beauty is that you can quickly find the angle (or radians) if you see "sin(x)=value", and you want
the associated angle "x" (or in radians) for which that equation holds.
-Example:
tan(x)=4/3. Then you know that tan-1(tan(x)) = tan-1(4/3) =x (in degrees or radians).
Using a calculator, then sin, cos, tan, and arcsin, arccos, and arctan or often directly availble, or you need
to "switch" the mode on that calculator to something like "inv" first, in order to get the inverse functions.
Also note that often the mode of your calculator can be in "degrees" or "radians" too.
Most often, you are looking for the angle in degrees, so in this example the answer is:
tan-1(4/3) = (about) 53 degrees.
-Example:
Suppose sin(x)=0.866
So, what is "x" (in degrees)? Maybe you need to switch the mode of your calculator into "inv" an "degrees".
sin-1(0.866) = x = (about) 60 degrees.
7. A few other bits...
Any time, when I think some new topic would fit in this note, I will place it in this section.7.1 The "Pythagorean theorem" works here too.
If you would take a look at figure 5 again, you see that the radius "r" sweeps along the circle.At any moment, the sides "a", "b" and "r", define a right-angled triangle, for which the "Pythagorean theorem" holds:
a2 + b2 = r2
Since:
sin(α)= b/r
cos(α)= a/r
then it follows that b=rsin(α) and a=rcos(α)
Thus:
(rcos(α))2 + (rsin(α))2 = r2
r2 (cos(α)2 + sin(α)2) = r2
And we may eliminate the r2 on both sides of the "="
cos(α)2 + sin(α)2 = 1
Which is usually written as:
cos2(α) + sin2(α) = 1
I will refer to that equation in a later note, so that's why I already mention it here.
7.2 The sine or cosine functions expressed in time and angular velocity.
For those interested in applications in physics, the following might be of interest.Mathematically, we talk about functions like sin(x) or sin(5x) etc...
So, like always up to now, we usually talk of a function of the variable "x".
If you then look at sin(nx) or cos(nx) graphs, it seems as if they are like a "snapshots" in time.
A physical system, on the other hand, is dynamic. In reality, any point on the "x-axis",
has a displacement which varies continuously with time, just like the small point on the y-axis
that you can see in figure 2.
So, the displacement of a certain point, varies with time, and that displacement thus can be described by sin(nt).
For a certain fixed point (but it can be any point), we know that it's displacement along the "y-axis"
can be described by sin(nt). Note that we focus here on the "sine", but we could just as easily have choosen "cosine".
The "n" in "sin(nt)" is tied to the property of how fast it "oscillates". We are almost there!
It's only logical to try to "link" that "n" to the physical properties of that system.
So, we have for a certain point:
Displacement along y = f(t) = sin(nt).
But it's "amplitude" (max displacement), does not have to be "1", and it can be any value "A". So:
Displacement along y = f(t) = Asin(nt).
The value "n" must have some sort of a direct link with the "frequency", as we have seen in a former section.
This is indeed possible. That "n" must be related to the frequency in a physical sense (often called "f"),
and it is: 2 π f. So we may write:
Displacement along y = f(t) = Asin(2πf t).
So, we are done here. Well, yes, but usually, the function f(t) is expressed in something
that's called "angular" velocity.
If you look at figure 2 again, the point on the circle, has a "uniform" motion, with a constant speed.
Suppose the "period" of completing one full circle is "T" seconds.
The circumference (or distance) of completing one full circle in "T" seconds is "2πr".
If T is short, then the frequency is high. And, if T is long, then the frequenct is low.
So, suppose T=5, then it takes 5 seconds to complete the whole cicle once. Note that 1/5=0.2.
Suppose T=0.2, then it only takes 0.2 seconds to complete the whole cicle once. Note that 1/0.2=5.
Indeed, the following relation exists between "T" and "f":
| f= | 1 - T |
Now, the angular velocity "ω", is a measure "how much angle" has been covered (between the radius and the x-axis),
for the particle that does the circular motion, does in a certain time.
Since the motion is uniform, that is constant, we can just as well take the "complete angle", that is the circle,
or "2π. It covers that in "T" seconds. So, ω is:
| ω = | 2π --- T |
Thus ω = 2πf
So, finally we can write:
Displacement along y = f(t) = Asin(ωt).
7.3 A listing of a few well-know goniometric relations.
I am not going to derive them, but here is a simple listing of some important goniometric relations.sin(π/2 - u) = cos(u)
cos(π/2 - u) = sin(u)
sin(u+v) = sin(u)cos(v) + cos(u)sin(v)
sin(u-v) = sin(u)cos(v) - cos(u)sin(v)
sin(u)+sin(v)=2sin((u+v)/2)cos((u-v)/2)
sin(u)-sin(v)=2cos((u+v)/2)sin((u-v)/2)
cos(u)+cos(v)=2cos((u+v)/2)cos((u-v)/2)
cos(u)-cos(v)=-2sin((u+v)/2)sin((u-v)/2)
cos(u)2 + sin(u)2 = 1
Or written as:
cos2(u)+sin2(u)=1
Or written as:
cos2u+sin2u=1
Some basic Geometry:
-Sine rule:
Suppose you have any triangle, with side lengths "a", "b", and "c".
And, we have the opposite angles α, β, γ, then:
| a --- sin(α) |
= | b --- sin(β) | = | c --- sin(γ) |
This is great, if you don't know one missing variable (like a side, or angle).
You can thus quickly calculate the missing one, for any triangle.
-Cosine rule:
For exactly the same situation as with the sine rule, we have the cosine rule
which states:
a2=b2+c2 - 2bc cos(α)
b2=a2+c2 - 2ac cos(β)
c2=a2+b2 - 2ab cos(γ)