This note is especially for beginners.

Maybe you need to pick up "some" basic "mathematics" rather quickly.
So really..., my emphasis is on "rather quickly".

So, I am really not sure of it, but I hope that this note can be of use.
Ofcourse, I hope you like my "style" and try the note anyway.

1. Finding the intersection with the y-axis.
2. Finding the intersection with the x-axis.
3. Finding all (local) minima and maxima that a function might have. Depending on the function, there might be
   0, or 1, or 2, or even more minima/maxima. For example, for a parabola, we have only one (local) minimum (or maximum),
   namely, the "top" of the "nose".
4. If it exist, investigate any 'asymptotic' behaviour. For example, f(x)=sin(x) does not expose an asymptotic behaviour,
   and our well-known parabola (a quadratic function) does not have it either. However, a function like f(x)=1/x does have it.
5. Identify all regions (along the x-axis) where a function exposes a 'climbing' character, and where it 'descends'.

1. Example 1.

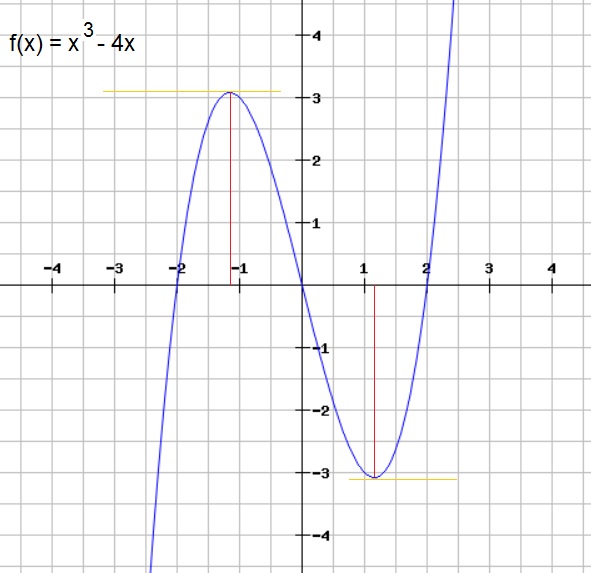
Our first example function, will be f(x)=x³ - 4x.

Below you see a plot of this function. Note that it crosses the x-axis at three points, the y-axis at one point,
and, that it has one local maximum, and one minimum. For the latter points: you see that "top" near x=-1, and
the crest near x=1? Those are the maximum and minimum we are looking for.

Figure 1. Plot of the function f(x)=x³ - 4x

1.1 Intersection of f(x) with the y-axis.

This one is really easy. Where f(x) intersects with the y-axis, it must hold that "x=0".
So:

y=f(x)=x³ - 4x. So, if we fill in x=0, then it follows that y=0.

Thus, for x=0 and y=0, the function intersects with the y-axis. It's the point (0,0) in the XY plane.

1.2 Intersection of f(x) with the x-axis.

Where f(x) intersects with the x-axis, it must hold that "y=0".
So:

x³ - 4x = 0   =>
x(x² - 4) = 0   =>

Thus: x=0 or x² - 4 = 0

We need to solve the second part: For x² - 4 = 0, it follows that x²=4, thus x=2 or x=-2

We have found the following x: x = 0, x = -2, and x = 2, for which it is true that y = 0.

So, at the following points in the XY plane, f(x) intersects the x-axis: (-2,0), (0,0), and (2,0).
Check the plot in figure 1, if this is indeed correct.

1.3 Finding the local minima and maxima of f(x) (if they exist).

Here is where we use the theory of note 5: the derivative of a function.

In note 5, we have found that the derivative of a function describes the "gradient" (or slope), of a tangent line.
At a maximum or minimum of the function, we have exactly the condition that the gradient is '0'.
Indeed, at those points the tangent line is parallel to the x-axis, with 0 slope.

Yes, you can try to picture several tangent lines along f(x) in figure 1, but you will only find two locations
where the gradient is exactly '0'.

So, we need to determine the derivative of the function, and find where it is '0'.

f(x)=x³ - 4x   =>
f'(x)=3x² - 4

f'(x)=0 means:
3x² - 4 = 0   =>
3x² = 4   =>

Thus:

x² = 4/3   =>

x=√ 4/3 or x= -√ 4/3.

So, we have found the following x's:   x=√ 4/3 and -√ 4/3 for which a maximum or minimum exists.

Now, these answer usually suffice. However, a teacher may request that you further calculate these square roots.
No problem, then you punch it into your calculator. And with a two digit accuracy (behind the dot) we find:

x = 1.15 and x = -1.15

Check in figure 1, if this is really correct.

Ok, we found the x's for the maximum and minumum. If it is requested to specify the points in the XY plane,
then for each of these two x's, we need to calculate f(x).

Now, you may feed in x = 1.15 and x = -1.15, into the equation x³ - 4x, but since those were approximations,
I personally would feed in x=√ 4/3 and -√ 4/3 into that equation.

I don't request to calculate it. I only want that you followed the reasoning sofar.
So, as an approximation:
you might say that for x = 1.15, we find that "y" is about -3.07, and for x = -1.15, we find that "y" is about +3.07.
Now, check the plot in figure 1, if this is a "reasonable" approximation.

But which point is the maximum, and which is the minimum? True, we have not answered this one.
If you have a plot, it is easy to answer. But if you do not have a plot, you still need to be able
to determine which is the local maximum, and which is the local minimum.

However, for now, if you followed the reasoning sofar, it's good enough for me.

1.4 Determining if f(x) exhibits asymptotic behaviour.

If you look at figure 1, and look at some larger values of "x", you see that f(x) is climbing steeper and steeper.
But is that asymptotic behaviour? No. You can keep calculating a valid "y", for any increasing value of "x".
True, the figure might suggest, that ultimately, it goes insanely fast upwards. Yes but you still can calculate an "y"
for a larger "x".

A vertical asymptote, is when you let x go near a value of x=a, where the function then really "threatens" to go to +/- infinity.

Or, when viewing the limit:

lim_{x ↓ a} f(x) --> +/- infinity

lim_{x ↑ a} f(x) --> +/- infinity

So, if we see a "singularity", or an "undefined territory" we might have asymptotic behaviour.
A good example is the function f(x)=1/x. See figure 2 below.

Figure 2. True asymptotic behaviour of f(x) when x nears '0'.



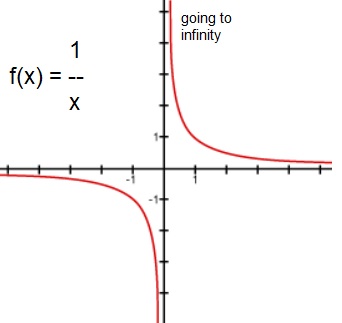
Here, if we consider "lim_{x ↓ 0} 1/x", or "lim_{x ↑ 0} 1/x", we see
that f(x) really goes to +/- infinity

1.5 Ranges of x, for which f(x) is positive and negative.

----INTERMEZZO:

In note 1, I introduced a few mathematical symbols. I like to repeat them again:

The examples below use, for example, '0' and '2' as some "markerpoint", but it can ofcourse be any number.
The whole purpose is to introduce the ">" (larger than), and "<" (smaller than) symbols, and a few other symbols,
which can be of great help to "label" certain ranges.

Examples:

x > 0	means: x is larger than '0'
x ≥ 0	means: x is larger or equal to '0'
x < 0	means: x is smaller than '0'
x ≥ 0	means: x is larger or equal to '0'
x ≤ 0	means: x is smaller or equal to '0'
-5 < x < 5	means: x is smaller than '5', but larger than '-5'
a ∧ b	means: a AND b
a ∨ b	means: a OR b
∀ x	means: for all x (in some set)
∃ x	means: there exists some x (in some set)

----END INTERMEZZO.

From figure 1, or the calculations of the intersections with the x-axis, we can identify the ranges of 'x',
where f(x) is positive (y>0), or where f(x) is negative (y<0).
If you like, refer to figure 1 again.

for x<-2, then f(x) is negative.
for -2 < x < 0, then f(x) is positive.
for 0 < x < 2, then f(x) is negative.
for x>2, then f(x) is positive.
f(x) = 0 for x=-2, x=0, x=2

2. Example 2.

This one is actually simpler than example 1. Here we are going to investigate a simple quadratic function.

Suppose we have the function f(x)=x² - 9x + 18.
Let's investigate it.

2.1 Intersection of f(x) with the y-axis.

Then we must have x=0, thus if we fill in '0' into the equation we find y=f(x)=18.

So, when x=0, we have y=18, where f(x) intersects the y-axis. It's the point (0,18) in the XY plane.

2.2 Intersection of f(x) with the x-axis.

Where f(x) intersects with the x-axis, it must hold that "y=0".
Thus:

x² - 9x + 18 = 0

Using the knowledge from note 3, we know that the solutions are:

x1=	-b + √(b2 -4ac) -------------------               2a

x2=	-b - √(b2 -4ac) -------------------               2a

You certainly may use those formula's to find both intersections.

However, I "see" that "x² - 9x + 18" can be quickly factored in (x-3)(x-6).

(x-3)(x-6) = x² - 6x -3x + 18 = x² - 9x + 18

So:

x² - 9x + 18 = 0   =>
(x-3)(x-6) = 0   =>

So, at x=3 and x=6, the function intersects with the x-axis. These are the points (3,0) and (6,0) in the XY plane.

2.3 Finding the local minima and maxima of f(x) (if they exist).

A parabola, has one maximum, or one minimum only. From note 3 you may remember that a quadratic equation
having "x²" has it's "nose" pointed downwards, so that's a minimum.
Also, a quadratic equation having "- x²", has it's "nose" pointed upwards, so that's a maximum.

So, with this function, we have a minimum "somewhere". To find it:

f(x)=x² - 9x + 18, thus:
f '(x)=2x -9

f'(x)=0   =>
2x -9=0   =>

Thus we have the minimum at x=4.5.

To find the corresponding y value: f(4.5)= 4.5² - 9x4.5 + 18 = 20.25 - 40.5 + 18 = -2.25.

So, at the point (4.5, -2.25) in the XY plane, the function has it's minimum.

2.4 Determining if f(x) exhibits asymptotic behaviour.

This one is for you. Do you think f(x) exhibits asymptotic behaviour?

That's it ! Hope you liked it.

The next note (note 7) is a super quick intro in the e^x and ln(x) functions.