A simple discussion on Quantum Mechanics and "Quantum Teleportation".
Date : 6 Januari, 2015
Version: 1.5
By: Albert van der Sel
Status: Ready.
Remark: Please refresh the page to see any updates.
Some nice theories from physics... Let's explore "Quantum Teleportation"...
Let's take a look at something that's really interesting...: "Quantum Teleportation" (QT)...
Quantum Mechanics (QM) is a real working horse in the microscopic arena of "field- and particle" physics.
But countless physicsts, philosophers (and who knows what else) broke their heads on the "interpretations" of QM.
Indeed, the stochastic character of QM, and the "descrete-ness" at times, is sometimes hard to "link" with "reality" (whatever that is).
Maybe modern insights may have shed lights on some effects, which were formerly not well understood (like "decoherence" replaces the "collapse"),
but plenty effects remain, which needs much more study.
Let's try to find out what "Quantum Teleportation" seems to be, and, let's try a very simple approach.
I suppose that I have to start with a general intro into QM. Otherwise, any talk about Teleportation, would not make much sense.
QT is the "transfer" of the Quantum state of an observable of a Quantum System, like the "spin" of a qubit,
to another Quantum System.
What a qubit is, will be explained later in this note, but for now, you may think of a particle like an electron,
which has a "spin" which is the superposition of two basis states ("up" and "down"), simultaneously.
So, the "state" of such a qubit "qA" in location "A", might be transferred to a qubit "qC" in location "C", which is for example 100km
remote from location "A".
Since only a "state" is transferred, QT has nothing in common with "Teleportation" of material objects.
As we will see later, this is not a "cloning" process, since we will see that the state of "qA" will be lost.
One prerequisite is the existence of a socalled non-classical "EPR" channel between entangled particles.
To actually transfer the information (bits) of the state of a qubit, also a classical channel is required too (like laser, EM radiation etc..).
So, since a classical channel is required too, no "laws" from Einstein's relativity theories are challenged or broken.
Notes:
Note 1:
Although I consider this humble note to be "reasonable" for it's content, it has to be labeled to be "fun stuff", since creating a (hopefully)
entertaining note, is actually my main motive. But, I really want it to be informative as well.
Note 2
The following classical article, published in 1993:
Teleporting an Unknown Quantum State via Dual Classical and Einstein–Podolsky–Rosen Channels (March, 1993)
by Charles H. Bennett, Gilles Brassard, Claude Crépeau, Richard Jozsa, Asher Peres, and William K. Wootters,
really started to set the QT train in motion. It's widely regarded as the classical article on QT.
You can find that article here (researcher.watson.ibm.com).
Contents:
Chapter 1. Just a few milestones, to get to the notion of the "wavefuction"..
1.1 Schrödinger's equation
1.2 Quanta.
1.3 Double slit experiment: interference patterns.
1.4 Superpositions, and wave-packets
Chapter 2. Hilbert space/Vector space. Or, the representation of a "state".
2.1 General representation of a "state vector"
2.2 Pure states and Mixed states
2.3 Collapse of the State Vector, or Decoherence, or MWI, or something else...
2.4 Example of a 2 statevector: representation of a "qubit".
Chapter 3. Quantum Information versus Classical Information.
Chapter 4. Collapse of the statevector replaced by Decoherence.
Chapter 5. Some remarks on Commuting/Non commuting observables & Heisenberg & measurements.
5.1 Commuting and Non commuting observables.
5.2 Heisenberg uncertainty principle.
Chapter 6. Product states and Quantum Entanglement.
6.1 Simple "pure states" and simple "seperable states".
6.2 Quantum Entangled states.
Chapter 7. Quantum Teleportation.
7.1 Original setup.
Chapter 1. Just a few milestones..., to get to the notion of the "wavefuction".
1.1 Schrödinger's equation
It was formulated (around 1924) by 'De Broglie', that there exists a "relation" between momentum (p) and wavelength (λ), in a "universal" way.
In fact, it's a rather simple equation (if you see it), but with rather large consequences. It's this: p = h / λ (where h is Planck's constant).
Here, λ is the "wavelength" of the "entity" (like a particle).
Now, "momentum", at that time, was considered to be a true 'particle-like' property, while 'wavelength' was understood to be a typical
'radiation-like' property, which stuff like radio waves (and other waves) display.
The formula of De Broglie, is quite amazing really. The conseqence is thus, for example, if you have a particle like an electron flying around,
you can associate a "particle like property" like momentum to it, but a "wavelenght" too.
So, what's going on here? Do we have a "matterwave" or something?
It didn't fully came out of the blue, ofcourse. A few years before, scientists (most notably Planck and Einstein) independently found clues
for the opposite, so to speak. Namely, that radiation at certain experiments, seemed to behave like matter.
It seemed that radiation displayed to have "momentum" as well.
Planck and Einstein found in some observations, that radiation exibited a "corpusculair" character, like in that radiation seemed to be
emitted in "quanta" (discrete energy packets).
But not only that, it seemed that those quanta possessed "momentum" too, as was observed in certain experiments.
So, in a way, both sides were covered now. It was puzzling. People started to talk about the "particle-wave" duality, as if in certain circumstances,
radiation behaves like matter, but other circumstances, matter behaves like radiation.
It must be said that the effects are observed in the microscopic Domain. Indeed, QM seems to operate (or is effective) on a small scale.
Inspired by this and other stuff, around 1926, Erwin Schrödinger published a mathematical equation about the evolution, that a quantum system
undergoes with respect to time, when that system happens to be in some sort of force field.
This quantum system is represented by a "wave function" Ψ (r,t), which will be explained in a minute.
The quantum system (like a particle) has certain characteristics, like it's position. It has been found that the evolution
of such characteristic (like the position) can be found, using the Schrödinger equation. The equation goes like this:
| iℏ |
∂ Ψ(r,t)
--------
∂ t
|
=
|
Ĥ Ψ (r,t)
|
Note: this is a "condensed" notation. If the Hamiltonian "H" is expanded, kinetic- en potential Energy terms get visible.)
The "ih" can be considered to be a constant for now. What the equation really says is this:
the change of the system in time (notated by ∂ Ψ (r,t)/ ∂ t), is the effect of the Hamiltionian "Η",
where the Hamiltonian "H" just stands for all forces and fields operating on the system.
It should make sense, doesn't it? A system changes in time due to the forces or fields acting on it.
Note: ∂ Ψ (r,t)/ ∂ t means that small delta's in time occurs, and the cooresponding change on the position (r) of the system, is a result
of the acting Energy on it..., or the Hamiltonian on it..., or the effects due to kinetic and potential Energy...
Usually, it is supposed to be applied to microscopic systems, like for example elementary particles etc..
However, in our macroscopic world there are similarities too: if you apply a force to a ball, it starts to roll.
Now, here is the crux of Schrödingers theorem: the solutions to the equation are wave equations like Ψ(r,t)=A . e-iωrt
So, believe it or not, such solutions are thus indeed wave equations.
Actually, the Schrödinger equation applies to a "quantum system", for which a good example would be a particle.
Now, this too suggests that a particle is sort of "smeared out" in space. However, such a view was never fully satisfactory.
After many other publications, conferences etc.., during the late twenties, and thirties of the former century, most physicists gradually
adopted the view that the wave function Ψ, can best be viewed as a probability distribution of the particle in space.
This actually means that it is not as much viewed as a "true wave", but should be better viewed as the likelyhood (chance) of finding the particle
at a particular place.
For example, the solutions of Schrödinger's equation applied to the Hydrogen atom, shows "electron orbitals", which are "distributions" of the electron
around the atomic nucleus (instead of circular orbits). Maybe you like to "google" on that further.
1.2 quanta.
Photo electric effect:
One of the many experiments that shows the quantum nature of light (or in general, ElectroMagnetic radiation), is the "Photo electric effect".
The experimental setup, is rather simple. But it's fair to say that the results of such experiments were a large stimulus for Quantum Mechanics.
These sorts of experiments were performed in the late 1800's and early 1900's, and clearly showed the "breakdown" of the classical field theories
like ElectroDynamics from Maxwell.
In short it is this: of you shine light on a sheet of metal, under certain conditions, electrons get's freed from that metal.
If the frequency is too low, it will not happen. No matter how intense that light is, it will not work.
Only if you use a very precise frequency, electrons will be emitted. That happens even when the intensity is very low.
Such a observation is not in accordance with classical theories: if you shine light with a very high intensity (very bright), a lot
of energy is poured in, and it should expell electrons of the metal. But none is freed.
Now, if the intensity is very low, but of a certain freqency, electrons will be emitted from the metal.
It was percieved as really strange (at that time). It was not in accordance with "continuous wave theory" like the one from Maxwell.
Around 1905, Einstein came with a good explanation (partly based on thoughts of Planck). Instead of a "continuous wave", Einstein proposed
discrete packages, or quanta, or photons, with a precise Energy Ephoton=hν, where h is Planck's constant, and ν is the
frequency of the radiation.
So, if such a quantum has an Energy that is equal or higher than the "binding" energy of outer orbit electrons, it is able to knock it out
from the metal.
Einstein's reasoning explained why the energy of freed electrons was dependent only on the frequency of the incident light and not on its intensity.
Simulation:
I recommend to download a small 'simulation' program (from colorado.edu), which illustrates the 'photo electric effect' brilliantly.
If you go here you can download it, and run it on your workstatstion.
But you need java (since the program is a .jar file). If you have it, then use for example "sodium", and vary the frequency from red to violet,
while at each colour (freqency) also varying the "intensity" of that light.
While this example has no direct link to "wave function", it highlights another aspect of QM, namely that some entities, or properties,
come in "discrete" steps. This does not mean that QM deals with "discrete" properties or entities only. Oh no!
However, it's an example of how QM can differ from "continuous classical theories".
1.3 Double slit experiment: interference patterns.
Again, here we have a relatively simple experimental setup. However, in some cases, the results are quite puzzling.
But, generally speaking, the experiment is a strong "plus" for wave-particle duality, as we will see.
Please take a look at figure 1. The picture in the middle, looks like how Thomas Young performed his experiment, in the early nineteenth century.
He used an ordinary light source, and a screen with two narrow slits.
he light emitted, will pass through those two narrow slits. Then, on a screen in the back, an "interference pattern" is shown, that is,
bands of lighter and darker regions can be observed.
At later times, these experiments were repeated, however this time using "true" particles, like electrons or neutrons.
Amazingly, a similar "interference pattern" is then observed.
Fig 1. The double slit experiment.
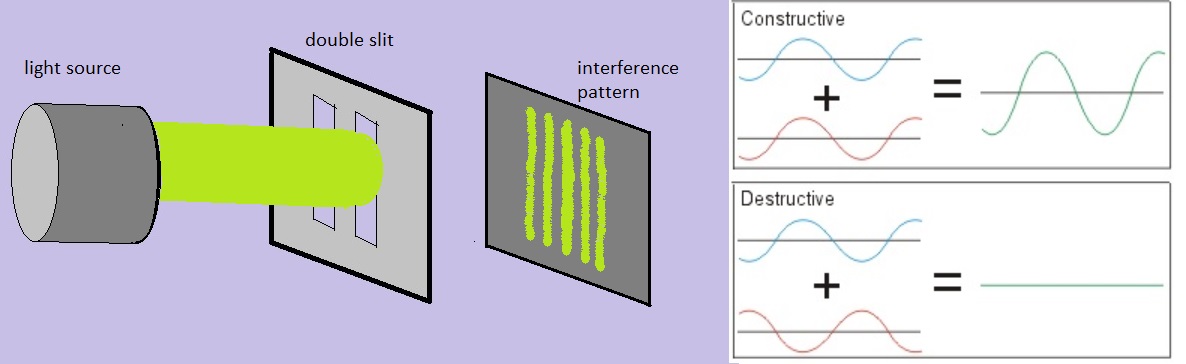
At this stage, we have to bypass certain angles to approach stuff, like using Heisenberg theorems, or viewpoints from "weak" measurements.
However, what we are going to see in a minute, is already spectacular enough. But let's start with an easy explanation.
=> 1. The "classical wave" approach:
Using light, and the classical wave interpretation, the results ("interference pattern") is as expected.
When light passes the two slits, at such a slit, it will be "defracted", and a spherical wavefront travels to the screen.
But keep in mind that there are two slits. Now, the waves are "sinusoidal" and have a certain fixed wavelength.
Even without calculations whatsoever, you can imaging that those waves travel different lengths, before they reach the screen in the back.
Now, take a look at the right image of figure 1. In some cases, waves may "cancel out", because at a certain point at that screen,
it holds that the wave from slit 1 happens to have a max amplitude, while the wave from slit 2 is exactly the opposite. Therefore the sum
of those waves cancels out (the centre of a dark region).
At other points on the screen, it holds that the wave from slit 1 happens to have a max amplitude, while the wave from slit 2 is max too.
This will then be the case for the centre of the bright bands on the screen.
The whole effect is just due, by the fact that the waves from slit 1 and 2, have travelled different distances, where at some points,
it will be "n x λ" (n as an integer number), and thus they amplify (the center of the bright bands).
At other places it will be "½ x n x λ", so the maxs and mins of the waves, cancel out (the center of the dark bands).
And ofcourse, there are regions where the waves partly positively or negatively add up (regions between the bright and dark bands).
=> 2. Using light again, but now we use the "quanta of Einstein" approach:
Here, it gets interesting if we lower the intensity. So, suppose we have a situation where occasionally photons are emitted.
Next, we observe the screen in the back. Now, we can see the small "impacts" which at first sight, are randomly distributed on the screen.
However, as time goes by, we see that an interference pattern builds up, exactly as we saw above.
This is not so easy at all. There was no way that a particular photon, could interfere with another photon. No, the intensity is so low, that they
are emitted one after the other, with sufficiently large "gaps" between those emissions.
The following may seem unbelievable (at first). Many physicists say that the photons are interacting with themselves, within their own wave packets.
to produce the interference pattern.
So, you might be tempted to suppose that a quantum goes through one slit. However, the best view is that such a quanta goes through both slits simultaneously.
This is difficult to reconsile with a "matter/quantum - like" view of radiation.
But there is no good alternative to explain the "interference pattern", if we use photons which are emitted one after the other.
So, it really looks like, in some strange way, that each photon is interfering with itself.
But hold on. Now let's see what happens if we do not use light, but "true" particles like electrons.
=> 3. Using particles:
This completely resembles what we have seen in (2). So, using a very low intensity, where electons one by one are emitted to the slits,
after a while, an "interference pattern" is build up.
Again, we must say that an electron goes through both slits simultaneously.
Unfortunately, at this stage, my choice of words is not very "optimal". This is so since there are some "intracies" with the "art of measurements",
like for example if we would use Heisenberg's theorems, or see what we have with commuting- and non commuting observables, and using "weak" measurements.
We have to leave that for a later moment.
However, what we discussed above, is really true, and at this point, quite amazing.
The discussion above partly reinforces the idea "particle-wave" dualisme. However, what it really shows is that we must "give up"
the idea of a photon or an electron having location.
The "location" of such an entity (like a photon, or electron) is not defined until it is observed.
You see that? We cannot even fully "escape" using a "probability distribution". The entity always seem to pass through both
slits. Here we get to a point where, even up to this day, physicists, philosophers, and many others, break their heads
on the results of this "seemingly" simple experiment.
Again, let's talk about such an electron again. It goes through both slits, so it acts like a wave? Thus, if so, you might then say
that it makes no sense to ask at which slit the electron passed through. Ok, so the electron behaves like a "wave" here.
I must say that this is a common interpretation among Physicists. However, not all physicists fully agree on that interpretation.
1.4 Superpositions, and wave-packets
If you have read section 1.3, you remember the electron that passed through both slits. It sounds very strange, weird maybe, but that's the best
quantum description of the event. If you say, in this case, the electron is like a wave, then at least that makes it more understandable that the
interference patterns emerge, which can be explained by the fact that the electron interfered with itself...
But, If it interfered with itself, it just "looks" like as if multiple 'waves' were 'superimposed'.
But there must be some connection with "probabilities" too.
The Schrödinger equation from section 1.1, might help us too, understanding the principle of "superposition".
It's just a "partial linear differential" equation, and there is nothing "fuzzy" about it at all.
Solutions for it, for several traditional "problems" have been worked out (like H-atom, particle in a box, a potential "well" etc...),
and it seems a nice starting point for QM.
Since the equation is linear, it means that superpositions (additions) of solutions, are solutions too.
Ask any mathematician which is nearest to you: he/she will absolutely confirm that !
So, if Ψ1 (r,t) and Ψ2 (r,t), are wavefunctions which are solutions for Schrödinger's equation, then
Ψ (r,t) = a. Ψ1 (r,t) + b. Ψ2 (r,t)
is a solution too (it's just math..., don't worry about it). In fact, any sum of solutions..., is a solution.
Now, a solution like:
Ψ (r,t) = ei(kr-wt)
is a solution indeed, but it looks like a "flat" wavefront, which does not "normalize"!
Because, if we calculate this:
∫ ALL SPACE d3r |Ψ (r,t)|2 = ∞
it means this: is if you would calculate, or actually "sum" the distribution of such "flat" wavefront
over all space, you will end up with an infinite number. That can't be good. That can't describe a particle.
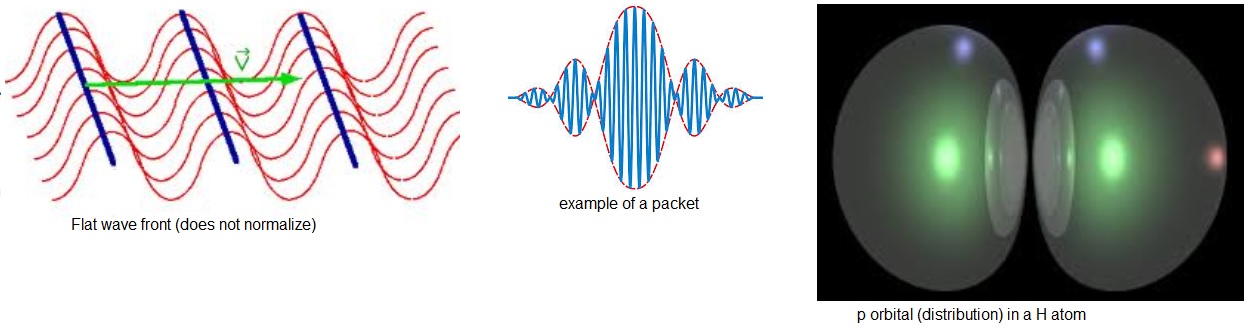
This is why physicists introduced the "Wave Packet". It's a superpostition too, but for a free particle, the components add up
in such a way, that the packet is grossly localized, like some sort of "gaussian" distribution, with a maximum, and it fastly diminishes
at the fringes. So, the following is a good solution:
Ψ (r,t) = 1/√ 2π ∫ ALL SPACE d3r g(k) ei(kr-wt)
where "g(k)" is a sort of gaussian function, which gives the wavepacket a maximum at it's "center", and quickly lowers the amplitude
as you move "away" from the packet's center.
However, theoretically, even at large distances, the amplitude is not "0", but it sort of asymptotically nears "0" the further you go.
It's very important to realize, that such a wave packet is actually a sum of superimposed (summed up) waves.
Often, it is called "superposition of states", where each state represent a certain "probability" that the particle actually resides in.
Those waves (states) of the packet are coherent, which means you can see them as solutions to a "harmonic occilator",
that is, sinusoidal-like waves in "shape".
Note:
That the component waves (states) of the packet are coherent, is often interpreted as that they do not "spread".
However, a wave packet in general. "naturally" spreads because it contains waves of different momenta and hence different velocities.
They all exist at the same time.
Remember the single electron that was used in the double slit experiment (1.3)? Here there was interference "with itself" meaning
interference from those superimposed waves.
Fig 2. Illustrating a Flat wave versus a wavepacket.
Let's now turn to a good way to "notate" or "describe" Quantum Systems (like a particle, photon, atom etc..), using the Dirac way
of handling stuff...
Chapter 2. Hilbert space/function space/vector space. Or, the representation of a "state".
Bohr, Bohm, Planck, Einstein, Pauli, Dirac, Heisenberg, Schrödinger, and many others, were the men who build
the original framework of QM, grossly in the period 1900-1938.
Originally, to work with QM, a "calculus" type of mathematics was used initially (like the partial differential equation of Schrödinger).
Somewhat later (in that same period), a "vector/matrix" type of approach to QM, was introduced. In many ways, that was in large thanks to Dirac.
This indeed made operations in QM much more uniform, and way better to understand (I think).
However, new work/discoveries as from, say, 1950 up to now (2015), were enormous. Also in the field of Interpretations of QM.
For about the latter: we certainly will see some stuff about "Collapse of the state vector", "Decoherence", "Many World Interpretation" (MWI),
and the "no-nonsense" interpretation (as some new physicists apparently seem to view QM lately).
Now, here is a little about Hilbert space/function space/vector space analysis.
Essentially, it's a "vector type of calculus". Ofcourse, if you dive into the professional literature, you will learn about
formal definitions on Hilbert spaces, complex spaces, conjugates, bras & kets, all of them with lots of theorems and collaries (and proofs thereof).
But we keep it simple ! We only want to crack Quantum Teleportation, and to understand what it is, and therefore, we only
need the info to get there.
What is a "ket" (Dirac) or "vector" anyway? It's often defined as an entity with both a magnitude and direction. However, visualizing a vector
in 2 dimensional space (a plane), or 3 dimensional space, is really easy.
Take a look at figure 3, where we see a picture of a point in space (1,2,3), and a vector "pointing", from the origin "O", to that point.
Fig 3. A vector in R3 (3D space).
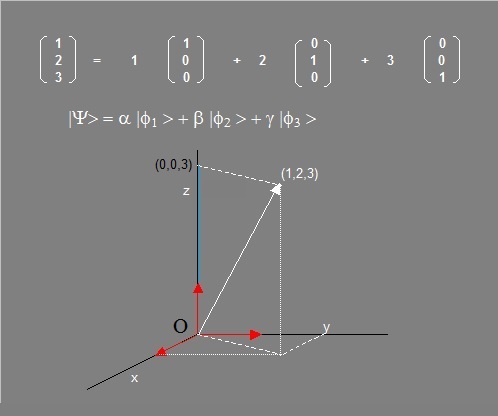
In figure 3, you see the vector (1,2,3) "going" from the origin "O" to the point (1,2,3) in space.
Most interesting is the fact, that we can say that to reach (1,2,3), we need to do "1 unit step" in the x direction, then "2 unit steps" in the y direction,
followed by "3 unit steps" in the z direction.
With a little imagination, you see the "unit vectors" (1,0,0), (0,1,0) and (0,0,1) positioned along the x, y, and z directions, respectively.
So, the vector (1,2,3) is equal to:
(1,2,3) = 1 x (1,0,0) + 2 x (0,1,0) + 3 x (0,0,1).
2.1 General representation of a "state vector"
Remember the "superpostion of waves", or "superpostion of states" from section 1.4?
Indeed, the quantum system (like a particle) is in een superpostion of such basis states.
Vector calculus provides a natural way to describe a quantum system in that way. Note that we now go to one of the "true" hearts
of the original (1900-1950) formulation of Quantum Mechanics!
So, if we let the states that all together form the superposition, be represented by basis vectors, then we can represent the Wavefunction,
or statevector, of a quantum system, in the following way:
|Ψ > = c1|a1 >+ c2|a2 >+...+ cn|an > = ∑ ci |ai >
where |a1 >, |a2 > (etc..) are n (ortogonal) eigen- or basis vectors (n=2,3,4,5...)
Instead of fully writing down all unit vectors of the superposition, often the Greek ∑ "summation" symbol is used, to denote exactly that.
Those basis vectors are often callen "eigen states".
So, a quantum system then, written in vector notation (the State vector), generally is a superposition of those "eigen states".
This is truly a core concept in the framework of Quantum Mechanics. Another one is the "measurement problem", which I will illustrate
using an example of what we have learned in this section, namely using the description of a "qubit". But, first something "special"....
A little more on "superposition":
The interpretation of "Superposition" in QM, is still a subject of debate, starting from the very first concept
of the idea in the early days of QM, all the way up to today.
When you see an equation as something like:
|Ψ >= α |0> + β |1>
where |0> and |1> are "basic" vectors, it looks like a simple vector superposition.
But, something weird is going on. We only know that |Ψ > is |Ψ >.
Only when a measurement on the observable (which |Ψ > represents) is done, we will find
either |0> or |1>. The corresponding probabilities for finding such basic state (eigenstate), must adhere
to the relation |α|2 + |β|2 = 1, because the sum of all probabilities
must add up to "1".
The phrase "only when a measurement is done, we will find one of the eigenstates", is amazing.
Suppose you find the state |1>, then what happened with |0>?
So, what is this? Does |Ψ > collapses into one of it's basis states (eigen vectors), or is it
the principle of decoherence which is at work here? Indeed, the "measurement problem" is key in
all interpretations of QM.
As another thing: Many physicists accept the idea that, unmeasured (or unobserved), |Ψ > written as
|Ψ >= α|0> + β|1> means that |Ψ > "exists" as |0> and |1> at the same time.
However, such an idea introduces it's own difficulties.
Even in such simple discussion as we see here, it's not too strange that the seemingly intrinsic
probabilistic behaviour we see in QM, might lead to idea's of "parallel universes".
That is: at an observation of |Ψ >, you might found |0>, but you might also have found the state |1>.
So, why not rephrase the matters like this: In one Universe you found |0>, and in another you found |1>.
However, such an interpretation is only shared by a lower number of Physicists.
In general, "superposition" is generally accepted among Physicists, and the substates exists simultaneously.
In math (Dirac notation), you may write it as an expansion of eigenstates, as a mathematical tool.
In that sense, it works. However, there still remains the issue of interpretation of such description.
2.2 Pure states and Mixed states:
A few words on Pure states:
While you might think that a completely defined state as |0 >, is pure, it holds in general for our
well known superpositions.
An example of an "superpositional" state, can be this:
|φ> = a1|u1> + a2|u2> + a3|u3>
You may also view a "pure state" as a single state vector, as opposed to a mixed state.
So, even at this stage, we already may suspect what a mixed state is.
Thus "pure states": We have seen them before in this note, sofar. They may be represented by a (Ket) vector.
A mixed state is a statistical mixture of pure states, while superposition refers to a state
carrying some other states simultaneously.
Although it can be confusing, the term "superposition" is sort of reserved for pure states.
So, our well-known qubit is a pure state too: |φ> = a |0 > + b |1 >
Or as a more general equation, we can write:
|φ> = Σ ai|ui>
This is a shorthand notation. Then i runs from "1" to "N", or the upper bound might even be infinite.
Usually, such a single state vector |φ>, is thus represented by a vector or "ket" (|>) notation,
and is identified as a certain unknown observable of a single entity, as a single particle.
So, a pure state is like a vector (called "ket"), and this vector be associated with a state of one particle.
A pure state is a superposition of eigenstates, like shown in equation 29.
Other notes on pure states:
Such vectors are also normalized, that is, for the coefficients (a1, a2, etc..), it holds that
|a1|2 + |a1|2 + ... =1
It's also often said that a pure state can deliver you "all there is to know" about the quantum system,
because the system's evolution in time can be calculated, and Operators on pure states work as "Projection" operators.
In sections above, we have also seen that the coefficient ai can be associated with the probability
of finding the state to be in the |uai> eigenstate (or basisvector) after a measurement has been performed.
In general, an often used interpretation of |φ>, is that it is in a superposition
of the basis states simultaneously.Then, the "keyword" here is "simultaneously".
However, this interpretation depends on your view of QM, since many "interpretations" of QM exist.
But "superpostion" will always hold, and is a key term of a pure state (like equation 29).
When you would insist on the qualifying phrase "a pure state gives us all there is to know", then probabily
(or maybe) known coefficients are required too, like for example with:
|φ> = 1/√2 ( |0 > + |1 > )
Note that some authors treat it that way.
But in general, undetermined coefficients are OK too. As long as we can talk of a "ket", we have a pure state.
Furthermore, it is required that the inner product of |φ> with it's associated "bra", is normalized,
that is, has a "unit length". That is, the inner product returns the value "1". Thus:
< φ |φ> = 1
If we have a Pure state, decribed as a superposition of eigenstates, there is a word of care
about interpreting it as a linear combination. In fact, we only know that |φ> = |φ>.
That's really it. Only when an observation is done, we find some of the eigenstates.
A superpostion is really something fundamental in QM, which has a mathematical description as a
summation (or expansion) of eigenstates. However, we only know that |φ> = |φ>, and no more.
The expression "linear combination" therefore, is subject to interpretation in QM.
A few words on mixed states:
A "mixed state", is a mix of pure states.
Or formulated a little better: a probability distribution of pure states, is a mixed state.
It's an "entity" that you cannot really describe, using a regular Ket statevector.
You must use a density matrix to represent a mixed state.
Another good description might be, that it is a "statistical ensemble" of pure states.
So we can think of mixed state as a collection of pure states |φi>, each with associated probability
density ρi, where 0 ≤ ρi ≤ 1 and Σ ρi = 1.
It cannot be stressed enough, that a linear superposition is not a mixture.
Mixed states are more commonly used in experiments.
For example, when particles are emitted from some source, they might differ in state.
In such a case, for one such particle, you can write down the state vector (the Ket).
But for a statistical mix of two or more particles, you cannot.
The particles are not really connected, and they might individually differ in their (pure) states.
What one might do, is create a "statitistical mix", what actually boils down in devising
the density matrix.
The statistical mix, is an ensemble of copies of similar systems, or even an ensemble with
respect to time, of similar quantum systems
So, you can only write down the "density matrix" of such an ensemble.
In equation 3, we have seen a "product state" of two kets. That's not a statistical mix, as we have here
with a "mixed state".
In a certain sense, a "mixed state" looks like a classical statistical description, of two pure states.
When particles are send out by some source, say at some interval, or even sort of continuously,
it's even possible to write down the equation (density matrix) of two such particles which were emitted
at different times. This should illustrate that the component pure states, do not belong to the same
wave function, or Ket description.
You might see a "bra ket-like" equation for a mixed state, but then it must have terms
like |φ > < ϕ|, which indicate that we are dealing with a "density matrix".
In general, the density matrix (or state operator) of a (totally) mixed state, should have a format like:
ρ = Σ ρi |ui > < ui|
Hopefully, you can "see" something that "looks" like a statistical mixture here.
An example:
Here is an example that "describes" some mix of two pure states |a > and |b >:
ρ = 1/4 |a > < a| + 3/4 |b > < b|
Note that this not an equation like that of a pure state.
Ofcourse, some ket equations can be rather complex, so not all terms perse need to have to be
in the form |φ > <φ|. Especially "intermediate" results can be quite confusing.
Then also: by no means this text is complete. That's obvious ofcourse. For example, partial mixed systems
exist too, adding to the difficulties in reckognizing states.
A certain class of states are the socalled pseudo-pure families of states.
This refers to states formed by mixing any pure state, with the totally mixed state.
So, please do not view the discussion above, as comprehensive description of "pure" and "mixed" states,
which is certainly not the case here.
2.3 Collapse of the State Vector, or Decoherence, or MWI, or something else...
From the former section, we know how to represent a State vector as a superpostion of "eigen states" (unit vectors).
But, at a measurement, "something" happens.
As we talk about pure quantum systems here, if we do not observe it, we actually do not know the state of that system,
only that it is in a superposition of (possibly) many states at the same time.
Remember the electron we used with the double slit experiment of section 1.3? It seemed that it passed both slits.
We even had to give up our notion of "clear path" or "clear trajectory" here.
Now, the following might not strike you hard, initially, but it's really something!
Suppose I place a small detector at one of the slits, say slit 1. Maybe I see a reading from my detector, meaning I have detected
the electron.
There won't be ever a interference pattern at the screen in the back.
Since I have located (or measured) the position of the electron, the "superposition" of all possible locations of the wavepacket
suddenly collapsed into a specific location, one of the possible eigenstates of that observable.
There are many other examples. The next one is a bit "blown up", but I want to make a point clear, even with an exeggerated example.
Suppose we send out a photon. We should regard it (for now) as a sperical wave, since we do not know anything of it's location.
Now, somewere in space, I have located a detector. If I find a reading, meaning I found (detected) the photon,
all posible locations "collapsed" into that single point.
As a more quantitative and realistic example:
Suppose I have the following 2 state quantum system:
|Ψ > = a . |a> + b . |b>
The system is in a superposition (or linear combination) of the eigen vectors |a> and |b>.
The coefficents "a" and "b" should determine the actual state of the system. However.., are we really allowed to talk that way?
QM tells us that we only know that |Ψ > is in a superposition of the eigen vectors |a> and |b>.
And we have not observed, or measured, anything yet!
Now, just as was the case with the electron, if we perform a measurement on the system, then we always find
the system to be in:
state |a> or in state |b>.
This might be percieved as quite weird.
Actually, some folks formulated it this way: our measurement "destroyed" the former quantum system. It (the quantum system) is something else now.
This is very close to the famous "measurement problem" in QM. It seems that our measurement was quite "disturbing" to the system.
Note: many people also call it a "strong measurement", or "perturbative measurement".
Did you noticed the "collapse of the State vector"? From |Ψ > = a . |a> + b . |b>, the system collapsed into either |a> or |b>
The stuff clearly shows us that QM is probabilistic in nature.
Moreover, experiments have shown that those coefficients (a and b) relate to the probability of finding the system in state |a> or in state |b>.
Then, since the probability of finding the state (after measurement) to be in |a> or |b>, must be "1" (or 100%).
Ofcourse, we can only find |a> or |b>, so the total chance added up, must be 100%.
However, the chance to find |a>, or to find it in |b>, is less than 1. It could be (for example) 30% and 70% respectively.
This can only be effectively determined after many experiments and simply count how often you have found |a> or |b>.
The only thing we really can say is this: all probabilities added, must be "1" (or 100%), and mathematically this equates to:
|a|2 + |b|2 = 1 (or 100%)
The interpretation of this phenomenon has long been a true issue for physicists and other scientists like philosophers.
It is still not fully understood, however, the socalled "Decoherence theory" provided us with a somewhat simpler way to digest it.
I like to touch on "Decoherence", a bit later on.
What we have seen here, is often called "The Copenhagen Interpretation", and it's great if you would google somewhat further on this.
It should be clear, that once a quantum system "collapsed" (or decohered) into an eigen vector, and you would immediately perform
a measurement again, then you will find that same eigen vector again. At least, that would be obvious from the theory presented thusfar.
2.4 Example of a 2 statevector: representation of a "qubit"
We already have seen the statevector of a two state system. This is also often called a "qubit" as a shortage of "quantum bit",
since "qubits" are used in the new technique of "Quantum Computing".
Here is a general representation:
|Ψ > = a1 |a> + a2 |b>
where |a> and |b> are ofcourse the eigen states (base unit vectors), and a1 and a2 are just numbers (the coefficients).
Now, since qubits are used in quantum computing, the |a> and |b> vectors are often "rewritten" as |0> and |1>.
There are two reasons for that.
One is to emphasis the "computing" element, since in traditional computing, ordinary "bits" (0,1) are the most fundamental units, ofcourse.
Secondly, often particles with "spin" (we will come to that in a minute) are used, as the physical entities, and such a spin
can be "up" or "down", which is often expressed as |0> and |1>, or sometimes also as |↑> and |↓>
There is ofcourse an enormous difference between classical bits (used in regular computing) and "qbits".
- A regular bit can only be "0" or "1".
- A quantum bit, or qubit, is a superpostion of |0> and |1>, and those "span", in principle, an infinite number of resultant states.
You might still be amazed. Well, the different combinations, which two basis vectors can "span" (with coefficents where |a1|2 + |a2|2 = 1 ),
can be visualized as a circle. Please take a look at figure 4.
Fig 4. Ψ as all possible combinations of |0> and |1>: the Bloch sphere.
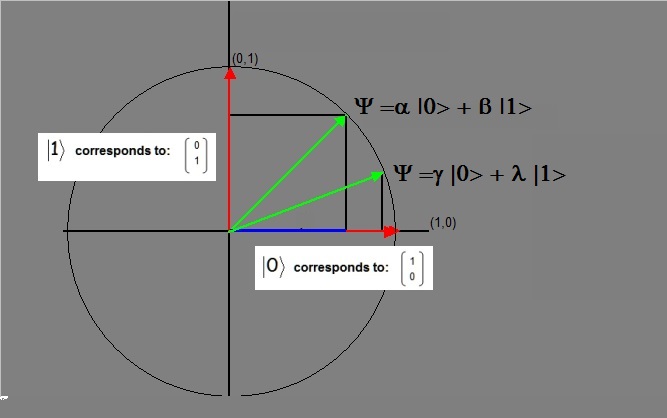
In figure 4, you see the two example Ψ Statevectors, in green. But these are just two examples. Any combination of the basis vectors |0> and |1>,
can "span" a Ψ statevector. That is, a1 |a> + a2 |b> will define a "circle" of possible eindpoints of the statevector.
Just keep in mind that a1 and a2 are numbers where the real part is < 1, that is, it needs to hold that |a1|2 + |a2|2 = 1.
Since we have two independent eigen vectors (|0> and |1>), it automatically defines this vectorspace as 2 dimensional (or a plane).
So, many folks visualize state |0> as the unit vector (1,0) (along the x-axis), and |1> as the unit vector (0,1) (along the y-axis).
In accordance with the theory of section 2.2, if you would perform a "measurement" on the qubit, you will find |0> or |1>
since the State vector will "collapse" or "decoheres" into one of those states.
Notes:
=> (1) What physical system can be a Qubit?:
Researchers might consider any system or entity that could potentionally work as a qubit, like for example molecules, atoms, ions, photons,
electrons, or any other particle or system. Thus, In principle, any system having an observable quantity which has at least two
eigen states, could be a "candidate" for a qubit. Again, unmeasured, the system would be in a superposition of those states.
Often, a spin 1/2 particle, is a good choice, like a "trapped" electron (quantum dot).
The big "enemy" of researchers is decoherence with the "environment", since that will alter the state of the qubit.
=> (2) Limitations:
As note before, this is not a "book" on Quantum Mechanics. Lot's of stuff is omitted in this note, and the concepts that are shown,
are simplified to a high level. For example, some "States" cannot be represented by by a "ket" or Statevector.
Chapter 3. "Quantum Information" versus "Classical Information".
We are now ready to compare some aspects of Quantum Information, to "Classical" information.
To narrow this down a bit, let's compare information of qubits to "classical bits".
Maybe not all of the items below will be immediately clear, but don't worry about it.
If you would consider a special case of Classical Information, like for example "bits" in a digital computer memory,
then some obvious observations can be made.
For example, the state of a computer register, is completely "known" at a certain moment. It might contain a bitstring like "1001 1101",
and this can be read, copied to tape, or disk, or another computer, or multiple disks etc..
=> (1) For Classical information, it is generally true that:
- you can read a register, or memory location, without altering it. It's "state" will not be altered.
- you can "clone" classical bits without any problem.
- you can "broadcast" classical bits to many destinations without any problem.
- If "power keeps on" and futher you do nothing at all, a memory location keeps that same bit string for years.
- if you don't know the state (content) of a register (or memory location) you can still copy it.
=> (2) For Quantum information, it is generally true that:
- You don't know the "value" of a qubit. It's "unknown". You only know it can be represented by a superposition of states.
- If try to "read" it, you interact with it, which "alters" it state.
- You cannot "copy" a qubit, since you cannot read or measure it precisely. It's a superposition, unless you "collaps" or "project" it.
- In general, if you "measure" a superposition of states, you get different outcomes all the time. At best you can get (over time) an expectation value.
- In general, if you "measure" a Quantum System, you get "a value "which you might consider as "classical" but it does not represent
the former (fuzzy) Quantum state. That is lost.
- Quantum Information cannot be fully converted precisely to classical information, and the other way around.
How about that? Would you (largely) agree with the listings above?
Before we go to "Teleportation", we need need some basic information about a fantastic quantum phenomenon: Entanglement.
Then, we need just a tiny bit more knowledge of vector calculus or "ket" algbra.
Then, in chapter 7, we will finally deal with the true subject of this note: Quantum Teleportation.
Chapter 4. "Collapse of the state vector" replaced by "Decoherence".
Next, we spend a few words on a couple of terms that were mentioned before: "Collapse of the State vecor (or wavefunction)" and "Decoherence".
=> Collapse of the Statevector / Copenhagen Interpretation:
In chapter 2, we have seen a few examples of the socalled "collapse of the Statevector". If an actual measurement on a quantum system is done,
out of many possible results, just one is "selected" in "some magical way".
An observable, initially in a superposition of different eigenstates, appears to reduce to a single value of the states,
after interaction with an observer (that is: if it's being measured).
This idea was much debated in the late 20s and 30s of the former century. Eventually the idea evolved into the socalled "Copenhagen Interpretation",
and while you could not say that it had true "advocates", it's a fact that many just accepted it as a "workable solution" for the Theory and observations.
(You may note that I completely bypass any thoughts about Hidden Variables, as an alternative for the collapse).
=> Decoherence:
In in the late 70s, 80s and early 90s of the former century, research got a renewed momentum to find a good "internal explanation" for the presumed "collapse".
This is no to say that much earlier, some folks (like Von Neumann in 1932) already investigated idea's that are quite close to "decoherence".
However, during the "renewed investigations", it was finally argued that a process called "decoherence" provides for a reasonable explanation
for just an "apparant" Collapse. There is no "sudden collapse", or "sudden reduction", it only appears to be so.
During that time, it was more and more realized that a quantum system is generally "embedded" in the environment. This is even true if you do not
measure anything at all. But it is especially true, if you let the quantum system interact with a "measuring device".
In QM, each state that contributes to the superposition of the State vector, needs to be in a coherent state.
Remember from section 1.4, that the waves (states) of the "wave packet" are coherent, which means they are similar like harmonics.
You can see them as solutions to a "harmonic occilator", that is, sinusoidal waves in "shape".
The theory of Decoherence states, that while the quantum system "nears" the measuring device, the different components entangles more and more with the many quantum systems
of the measuring device, (or in general: the environment), and a process called "einselection" takes place. It means that most entangled waves (or "coupled" waves) leakes out
to the environment, until a pure state is left over. This process is thus responsible for an apparent collapse.
Nowadays, it's "almost" fully accepted that "measurements" involve entanglement of the quantum system with the environment,
and the former idea of the sudden "reduction", or "collapse", of the statevector, is replaced by decoherence.
Especially Zurek created nice articles that go into depth in the theory of Decoherence, while it's still nice reading.
I can recommend this article (arxiv.org), although it's quice "spicy" (technical).
Other great stuff can be found here: Quantum Decoherence (www.ipod.org.uk)
Chapter 5. Some remarks on Commuting/Non commuting observables & Heisenberg & measurements.
Sometimes you may think that QM is kind of "fuzzy". Actually, it's generally speaking not "fuzzy" .
If you look at a wave packet (of section 1.4), a lot of waves are superposed, with a sort of gaussian probability distribution.
It might look "fuzzy", but it's just a superposition, and we can even capture it in an equation.
So is it really fuzzy? Probably not, but what might look "fuzzy" is the "probability distribution".
Such statements are not really exact. Besides that, different folks may have different interpretations too.
Please consider again the formalism of section 2.2, where we represented the Statevector (of a quantum system) as a superposition of eigenstates.
In such a case, if you observe the quantum system (or perform a measurement), then we find a eigen state with a certain probability.
That's not fuzzy, since you can find a well defined value. What does make people wonder, is that finding a certain value due to a measurement,
is that this is associated with a "probability". Indeed QM, is intrinsically "stochastic".
However, some say that the theory of "decoherence" removed the "stochastic" character of QM. That's not true, since the original superpositions
still are part of the theory. But, again, different folks may have different interpretations.
And, what we have not seen here much, is that at many places in QM, discrete "quantum numbers" play an important role.
Now, I need to make a little "refinement" on what I have presented sofar:
Actually, when we observe a quantum system, an "observable" is involved. This is an important term. In general, a quantum system (like a particle),
may have multiple observable "properties", like position, or momentum, or spin, or polarization etc...
Question is: if we measure for example the "spin" of a particle, then the statevector for that observable will collapse/decoheres to an eigen state.
So, did we now collapsed the "whole of the particle", or just that particular property? In general, this is not so easy to answer.
However, in some cases, it's not difficult. Suppose you measure the orientation of the spin of an electron, and you find the state "up" (|↑>),
then it's still an electron! However, that specific observable decohered (collapsed).
In some other cases, it's not so easy. If you "measure" the position of a photon, then it's "gone" (meaning that maybe some electron in the material of a screen,
absorbed the energy quantum, and was freed, or went into a higher atomic orbital..).
5.1 Commuting and Non Commuting observables.
How many observables may a quantum system have? Indeed. It can be quite a lot.
Only in the very most simplest case, an observable defines the state of of a Quantum system.
But in general, more observables are needed to "define" or "pin down", a quantum system. Just take a look at a particle. It has a
position in space (wave packet), a momentum, and possibly it may have a "spin" too.
Up to now, we have "acted" as if one observable defines a quantum system. Now, we know that in general that is not true.
Measurements on observables "A" and "E", can be interpreted as having Operators acting on those observables. Often, those Operators
get a similar naming as the observables (with an additional token like a circumflex, hyphen etc.., but that depends a bit really).
1. Commuting observables (operators):
It is said that operators (or the associated observables) commute if the following holds:
Â Ê Ψ = Ê Â Ψ
In the equation above, you see that in this case the order of taking measurements does not matter!
We are not going to mathematically prove it, but the following may sound plausible.
It can be true if both observables (State vectors) can be expanded (or written) in a common set of eigen vectors.
Often, people say that A and E have a "mutual eigenbasis".
Actually, it's a better way to describe that two observables "commute", if both can be measured simultaneously, with definite values
and thus both (sort of) more "pinned down" the state of the quantum system.
It's also often said that the observables are "compatible", which is the same as "commute".
Unfortunately, it's all pretty abstract for now. But if you believe that both observables have a "mutual eigenbasis", then both
can be measured and definite values can be found at the same time.
You can also say this:
- This is only so if Ψ is an eigenvector of both operators.
- Two observables can be known simultaneously only if they have a common set of eigen vectors.
2. Non commuting observables (operators):
There are also Non commuting observables (or Operators). It's also often said that those onservables are "incompatible".
Two incompatible observables cannot have a common set of eigenstates (no "mutual eigenbasis").
Say we have A and E again. It can be proven that it's simply not possible to find a well defined value for A, and a well defined value
for E at the same time (simultaneously).
Furthermore, the order of performing measurements now is relevant, and Â Ê Ψ ≠ Ê Â Ψ
Rephrasing Non commuting operators in "brute force language":
Gaining knowledge of one observable through a measurement, destroys information about the other.
3. Further explanation:
If Ψ really would be an eigenvector of both operators (observables), so both observables have a mutual set of eigenvectors
then you can hopefully see that measuring A and E would always produce an eigen vector in the same vector space.
Since finding an eigenvector was already a matter of probability, but the system stayed in the same vectorspace.
So, the second measurement will produce again an eigenvector with a certain probability.
But, it boils down to the fact that you can find precise values for A and E, even at the same time.
If the observables are incompatible, both have different eigenvectors. And a perturbative measurement on A, disrupts everything
so much, that the uncertainty in E increases highly. A perturbative measurement on E disrupts everything so much, that the uncertainty in A increases highly.
You cannot have precise values for both observables.
I realize that this is not a good attempt to try to explain the differences between commuting and non-commuting operators.
Using math, it could be explained way better. But I try to avoid math as much as possible.
Some examples:
- Adding numbers commute, since in any addition you can reposition terms as you like, e.g. a+b+c=a+c+b
- Rotating an object over two axes (thus two operations), does not commute. If you turn 90% along the x-direction,
and then 90% along the z-direction, will produce a different orientation of the object than the other way around.
- Position and momentum does not commute. If you measure precisely the position of a photon, the momentum is destroyed.
5.2 Heisenberg uncertainty principle.
Note:
Some historians have researched where the "principle" actually first originated.
They have reasons to believe that actually Pauli was first to express ideas of such content, while others see evidence
in papers of Wiener to believe that actually "Wiener was first...."
Sometimes the Heisenberg uncertainty principle is associated with the "precision of measurement".
That is not a good view, really.
Here I am not saying that there does not exists a "measurement problem" in QM. There absolutely exists a "measurement problem" in QM,
which constitutes one of the hearts of QM.
A remark on the measurement problem in QM:
If you would measure the temperature of a large swimming pool, your device will not (really) have any relevant influence
on the swimming pool. In fact, the measuring device is so small compared to that large body of water, that it is absolutely
correct to say that your measurement did not "disturbed" the swimming pool at all. It was not a "perturbative" measurement.
The large swimming pool was not changed by your measurement.
However, QM is used in the world of elementary particles, photons, atoms etc.. These quantum systems are very small,
and any measurement you perform, will be "perturbative" to some extend.
In fact, your measurement will change the state of the quantum system. And even one of the "core" descriptions in QM, namely
that a State vector "collapse" or "decoheres" to an eigen state when a measurement is performed, actually "sort of" confirms
that your measurement is "perturbative".
It's a core problem, and even up to this day, different perspectives are published in a whole range of scientific articles.
Note: "weak" measurements.
A "perturbative" measurement is also often referred to as a "strong" measurement.
Contrary to such "disturbing" measurements, in 1988 a couple of physicists published an article on "weak" measurements,
in which they stated that in principle, extremely weakly coupled measurements could be performed, which, run over a longer period,
could give information about the "undisturbed" quantum system.
This idea raised quite some debate in the scientific community, which is not over yet.
A remark on the Heisenberg uncertainty principle:
The Heisenberg uncertainty principle is simply build into QM. Once you deal with non commuting observables (or operators),
you "get it for free". In fact, it's really not directly related to the "measurement problem".
One of the most used example of the Heisenberg uncertainty principle, is when you consider the pair of "non commuting" observables
position (x) and momentum (p).
In fact, as from the moment that you proposed a "wave packet" to express the "position" of a particle, the "Heisenberg uncertainty principle"
will be build in automatically. It arises from the wave properties which are inherent in the QM description of nature. Really !
The Heisenberg inequality relation for position (x) and momentum (p) is:
Δ x . Δ p > ℏ / 2
It means that the more precisely the position of some particle is determined, the less precisely its momentum can be known,
and the other way around.
It has been proven, theoretically and experimentally, for many quantum systems.
For example, if you go to the following wikipedia article, and go to the "particle in a box" problem, the inequality will be derived in a fairly simple way.
And it's just based on the wave mechanics of QM ! So, as please see this example (wikipedia)
Please note that the derivation has nothing (!) to do with "precision" of measurements. It's just build deep in the description of QM.
Next, a discussion on "Quantum Entanglement" is on the list of "things to do".
6. Product states and Quantum Entanglement.
We already have seen some "State vector" examples. I will provide for a few more simple examples here, in a minute.
Technically, QM distinguishes between "pure states" and "mixed states" (and even others), which can be quite confusing, really.
Since this note is very simple, I don't go into that. What we have seen thusfar, are pure states since we just have
a "State vector" as linear combination of eigenvectors, which are in superposition simulaneously.
I want to keep that image, so to speak, as not to introduce too much complexity.
A mixed state is often a statistical mixture of pure states, where a more complex interference might be present,
and it has certain complexities in interpreting coefficients as probabilities.
Mixed states introduce an additional layer of complexity, and is often used in "ensembles" studies.
However, most Physicists say that "mixed states" can only be described using density matrices.
Here we keep it simple (and thus less general...).
6.1 Simple pure states and simple seperable states.
1. A few example of (simple/pure) State vectors:
- A state vector with a basis of two eigenstates (a qubit):
Ψ = a|0> + b|1>
- A state vector with a basis of three eigenstates:
|Ψ > = c1|φ1 >+ c2|φ2 >+c3|φ3 >
- A state vector with a basis of n eigenstates:
|Ψ > = c1|φ1 >+ c2|φ2 >+...+ cn|φn > = ∑ ci |φi >
2. A few example of "product states":
We will first take a look at the normal "product state". If we have two systems, and we want to describe their "joint state",
an outer product is used to accomplish that.
Suppose we have two qubits like:
|φ1 > = a|0> + b|1>
|φ2 > = c|0> + d|1>
then:
|Ψ> = |φ1 > ⊗ |φ2 > = ac|0>|0> + bd|1>|1> + ad|0>|1> + bc|1>|0> =
ac|00> + bd|11> + ad|01> + bc|10>
The equation above, is a way to describe the combined state of both qubits.
It's just a product state of all components, and those components are not further "correlated".
Note that for example |00> is no more than a short way to mean |0>|0>.
Actually, what we have seen above, is the "Quantum Way" for the following simple mathematical equation:
(a + b) x (c + d) = ac + ad + bc + db
Whenever you have a situation where it is possible to write:
|Ψ> = |φ1 > ⊗ |φ2 >
and |φ1 > and |φ2 > are any n-dimensional pure states, then we can speak of "seperable" systems,
since their joint state is a simple product of both states.
It's really just the same as the simple mathematical analogy, that:
"ac + ad + bc + db" is seperable into "(a + b) x (c + d)".
6.2 Quantum Entangled states.
"Entanglement" in Quantum Mechanics (QM) plays a crucial role here, so let's spend a few words on that subject now.
Here again, we describe two or more quantum systems (like particles, photons), with a sort of common state vector, like we
have seen above. However, this time, the systems are "not seperable".
That is, we cannot simply write it as a product state, like |Ψ> = |φ1 > ⊗ |φ2 >
It means that we cannot "seperate" the systems "just like that"!.
Their "intertwinement"is so high, that we speak of "correlated" systems, with respect to the "observable" (often spin, polarization).
Automatically, since we cannot seperate the individual states anymore, a measurement on one particle, affects the other as well.
That is the "crux" of "entanglement". Don't think lightly about that. Although it's a common feature in Nature, as we know now,
it has important consequences, and produces lot's of brain fire-crackers for "philosophers" and others who want to understand nature.
Just take a look at this. Supose two correlated particles are in close vincinity. Now, we move one of those system further and further away
from it's partner particle. It's commonly accepted that still holds that: a measurement on one particle, affects the other as well.
Now, if the distance is very large, even so large, that some sort of "signal" between the partners would violate the speed of light barrier,
then we might be very puzzled.
Indeed, it's experimentally established that both "collapse" to another state, simultaneously, even if their distance is larger
than some "magical" signal would need timewise. So, the partners cannot "inform" each other about a change in state.
This is the effect that Einstein called "spooky action at a distance...
Noteworthy is the article "Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?" (1935)
by A. Einstein, B. Podolsky, and N. Rosen which resulted in what later was called "The EPR paradox".
As the authors argue, a number of results of QM, seem to be inadequate to describe physical reality. As we can interpreted it now,
most of their arguments actually refer to the effects of entanglement, collapse of the state vector, and other aspects of QM.
It's certainly worth it, to perform a web search, and browse through some articles which explain the original article.
It's certain that the last words has not been spoken yet on entanglement, and many suggestions have been forwarded why we
still not fully comprehend it, like for example:
- We do not correctly describe the entangled state, and/or interpret it wrong.
- SpaceTime issues related to "Entanglement" are not (yet) understood.
- Strange "hidden variables" are at work here, and sadly, we don't known of those yet...
- Nature sometimes just works "non-local" in certain events. This is the non-locality principle.
There are some interesting studies to the "nature" of "what" exactly sort of "binds" the partners of an entangled system.
The "non-locality" principle is widely accepted. However, at this moment it does not deliver the "mechanics" of the strange binding.
In chapter 7, we will see that it is often called "The EPR channel" as a tribute to the famous EPR article.
Some further studies try to explain the EPR channels using further maths on Hilbert spaces, and the resulting "channel maps" thereof.
One consequence seems to be, that "time reversals" are neccessary to keep the theory consistent.
Needless to say, that if true, it would be very spectacular.
As an example, you might browse through this article (arxiv.org), but it's quite hard to read.
Other studies try a lattice approach. Still others, use any other concievable way to to pursue the EPR channel further.
One other amazing path, is the ER=EPR wormhole suggestion. Some folks have put forward, that at the Planck scale, wormholes exists,
at the ultimate smallest scale of SpaceTime. The EPR wormholes then, supposedly connect entangled particles.
However, many physicists are sceptical, and like much more "body" on those models. Many articles have appeared, pro and contra,
since the original ideas were published.
As an example, you might browse through this article (arxiv.org), but here too, it's not easy to read.
One thing is for sure though: physicists do not accept any "faster than light" signalling, to explain it.
(Note: Even in the case of Planck-scale wormholes, the theory uses "non-traversable" wormholes, or maybe, the theory leads
to non-traversable wormholes. This should evade superluminous signalling.)
A well known example of entangled particles:
Here is a well-known example, namely a singlet state of two particles (particle 1 and particle 2) with respect to their spin.
|Ψ1,2 >= 1/√2 . ( |↑1 ↓2> - |↓1 ↑2> )
So, the wave function above, describes the "common" state of such an entangled system with respect to their spin.
Do you see that it is a superposition of the states "|↑1 ↓2>" and "|↓1 ↑2>"?
If a measurement is done, and you find particle 1 to be "up" (↑1), then it follows that particle 2 must be ↓2.
Since "obviously", the wavefunction "collapsed" into state "|↑1 ↓2>", it automatically follows
that particle 1 is "up" and particle 2 is "down".
But both spins might take any value along a particular axis, as long as you have not measured it. This strange "thing" is a hard part of QM
to understand.
An entangled system may "exist" for some time, but often, quite quickly, a particle interacts with the environment, at which decoherence
will end the (two-system) entanglement. So, it's not easy to seperate the members of a singlet state, for example, hunderds of meters, or a few km's (or further) apart.
People working in the field of "Quantum Computing" often spend quite some time investigating how to "battle" Decoherence so that
they can preserve their qubits and gates for a longer period of time.
So, what do we have "qubit wise" now?:
1. One qubit:
|Ψ> = a|0> + b|1>
2. Two qubits:
The general state of a "two qubit system" is given by the quantum state:
|Ψ> = a00|00> + a01|01> + a10|10>+ a11|11>
Here, the system exists in the states |00>, |11>, |01> and |01>, at the same time (simultaneously).
We know that it is a "product state" of two single qubits, and it's "seperable".
3. Two strong entangled qubits (Bell states):
Two qubits (or more qubits) can be in an "entangled" state.
There are different possibilities here. Especially, the socalled "Bell states" denote strongly entangled systems.
You know that the "parts" of an entangled system might be seperated, in different regions, for example in different corners of a Lab,
or different rooms, or maybe 500m apart. Usually, folks use characters like Alice and Bob as two
imaginary persons, each holding one part the entangled system. That's why often a subscript "A" and "B" is added to a substate of the
superposition, to denote "where it is" (at Alice or at Bob). Be warned though, many folks just leave it out just as easily.
Here they are:
|ΨA,B >= 1/√2 . ( |0>A |0>B + |1>A |1>B )
|ΨA,B >= 1/√2 . ( |0>A |0>B - |1>A |1>B )
|ΨA,B >= 1/√2 . ( |0>A |1>B + |1>A |0>B )
|ΨA,B >= 1/√2 . ( |0>A |1>B - |1>A |0>B )
The most important to remember here is, for example, if you look at "|0>A |0>B", it means that
if the system would collapse into that state, it means Alice found |0> (down), and Bob must have found that too.
Notes:
Such "pure" maximally entangled states, could be used as a noiseless "EPR channel" (see below) in Quantum Teleportation.
However, the "sender" and "receiver" might only be able to share a "mixed" entangled state (noisy channel), due to the decoherence.
In most articles on entanglement and qubits, you might often see representations like we already know, and I mean like this example:
|Ψ1,2 >= 1/√2 . ( |↑1 ↓2> - |↓1 ↑2> )
Keep this one in mind.
Let's try Quantum Teleportation now...
7. Quantum Teleportation.
Finally, we are "ready" to get into Quantum Teleportation (QT).
This will be a relatively short chapter. This is so, since we already have covered so much ground above.
For example, we don't need to explain "qubits", "the state vector", "entanglement" etc..., anymore.
Quantum Teleportation is not about the "teleportation" of matter, like for example a particle.
It's about teleporting the information which we can associate with that particle, like the state of it's spin.
For example, the state of the system described by equation 1 above.
A collarly of "Quantum Information Theory" says, that "unknown" Quantum Information cannot be cloned.
This means that if you would succeed in teleporting Quantum Information to another location,
the original information is lost. This is also often referred to as the "no-cloning theorem".
It might seem rather bizar, since in the classical world, many examples exists where you can simply copy
unknown information to another location (e.g. copying the content of a computer register, to another computer).
In QM, it's actually not so bizar, because if you look at equation 1 again, you see an example of an unknow state.
It's also often called a "qubit" as the QM representative of a classical "bit".
Unmeasured, it is a superposition of the basis states |0> and |1>, using coefficients "a" and "b".
Indeed, unmeasured, we do not know this state. If you would like to "copy" it, you must interact with it,
meaning that in fact you are observing it (or measuring it), which means that it flips into
one of it's basis states. So, it would fail. Hence, the "no-cloning theorem" of unknown information.
Note that if you would try to (stronly) "interact" with a qubit, it collapses (or flips) from the superpostion
into one of the basis states.
Instead of the small talk above, you can also formally work with an Operator on the qubit, which tries to copy it,
and then it gets proven that it can't be done.
One of the latest "records" in achieved distances, over which Quantum Teleportation succeeded, is about 150 km.
What is it, and how does an experimental might look like?
Again, we have Alice and Bob. Alice is in Lab1, and Bob is in Lab2, which is about 100km away from Alice.
Suppose Alice is able to create an "entangled 2 particle system", with respect to the spin.
So, the state might be written as |Ψ> = 1/√2 ( |01> + |10> ), just like equation 3 above.
It's very important to realize, that we need this equation (equation 3) to describe both particles,
just as if "they are melted into one entity".
As a side remark, I like to mention that actually four of such (Bell) states would be possible, namely:
|Ψ1> = 1/√2 ( |00> + |11> )
|Ψ2> = 1/√2 ( |00> - |11> )
|Ψ3> = 1/√2 ( |01> + |10> )
|Ψ4> = 1/√2 ( |01> - |10> )
In the experiment below, we can use any of those, to describe an entangled pair in our experiment.
Now, let's return to the experimental setup of Alice and Bob.
Let's call the particle which Alice claims, "particle 2", and which Bob claims "particle 3".
Why not 1 and 2? Well, in a minute, a third particle will be introduced. I like to call that "particle 1".
This new particle (particle 1), is the particle which "state" will be teleported to Bob's location.
At this moment, only the entangled particles 2 and 3, are both at Alice's location.
Next, we move particle 3 to Bob's location. The particles 2 and 3, remain entangled, so they stay
strongly correlated.
After a short while, particle 3 arrived at Bob's Lab.
Next, a new particle (particle 1), a qubit, is introduced at Alice's location.
In the picture below, you see the actions above, be represented by the subfigures 1, 2, and 3.
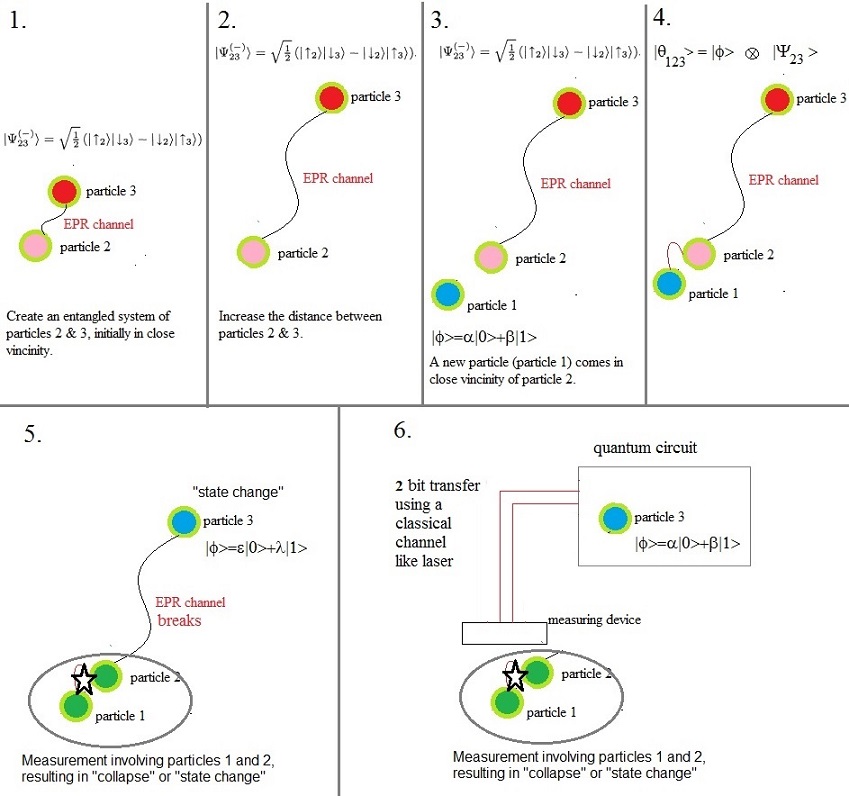
The particles 2 and 3, are ofcourse still entangled. This situation, or non-local property, is often also expressed
(or labeled) as an "EPR channel" between the particles.
This is presumably not to be understood as a "real channel" between the particles, like in the sense of a
channel in the classical world.
In chapter 2, we try to see what physicists are suggesting today, of which physical principles may
be the source for the "EPR channel/non-locality" phenomenon.
Let's return to the experimental setup again. Suppose we have the following:
-The entangled particles, Particles 2 and 3, are collectively described by:
|Ψ2,3> = 1/√2 ( |01> - |10> )
-The newly introduced particle, Particle 1 (a qubit) is decribed like we already saw in equation 1, thus by:
|φ1> = a|1> + b|0>
Also note the subscripts, which may help in distinguishing the particles.
At a certain moment, when particles 1 and 2 are "really close", (as in subfigure 4 of the figure above),
we have a 3 particle system, which have to be described using a product state, as in:
| θ123> = |φ1> ⊗ |Ψ2,3 >
Such a product state, does not imply a "strong" measurement or interaction, so the entanglement still holds.
Remember, we "are" still in the situation as depicted in subfigure 4 of the figure above.
We now try to rewrite our product state in a more convienient way. If the product is expanded,
and some some re-arrangements are done, we get an interresting endresult.
It's quite a bit math, and does not add value to our understanding, I think, so I will represent this endresult
in a sort of "pseudo Ket" equation:
| θ123> = |φ1> ⊗ |Ψ2,3 >
=
½ x [ Φ12 (-a |13 > - b |03 >) + Φ12 (-a |13 > + b |03 >) + Φ12 ( a |03 > + b |13 >) + Φ12 ( a |03 > - b |13 >) ] (equation 5)
=
½ x Φ12 [ (-a |13 > - b |03 >) + (-a |13 > + b |03 >) + ( a |03 > + b |13 >) + ( a |03 > - b |13 >) ] (equation 6)
Note the factor "Φ12".
We have managed to "factor out" the state of particles 1 and 2 into the "Φ12" term. At the same time,
the state of particle 3 "looks like" a superpostion of four qubit states.Indeed. Actually, it is a superposition.
Now, Alice performs a masurement on particle 1 and particle 2. For example, she uses a laser, or EM radiation
to alter the state of "Φ12".
This will result in the fact that "Φ12" will collapse (or "flip") into another state.
It will immediately have an effect on Particle 3, and Particle 3 will collapse (or be projected, or flip) into one
of the four qubit states as we have seen in equations 5 and 6 above.
Ofcourse, the Entanglement is gone, and so is the EPR channel.
Now note this: While Alice made her measurement, a quantum gate recorded the resulting "classical" bits
that resulted from that measurement on Particles 1 & 2.
Before that measurement, nothing was changed at all. Particle 1 still had it's original ket equation |φ1> = a|1> + b|0>
We only smartly rearranged equation 4 into equation 5 or 6, that's all.
Now, it's possible that you are not aware of of the fact that "quantum gates" do exists, which functions as experimental devices,
by which we can "read out" the classical bits that resulted from the measurement of Alice.
This is depicted in subfigures 5 and 6 in the figure above.
These bits can be transferred in a classical way, using a laser, or any sort of other classical signalling,
to Bob's Lab, where he uses a similar gate to "reconstruct" the state of Particle 3, exactly as the state of
particle 1 was directly before Alice's measurement.
It's an amazing experiment. But it has become a reality in various real experiments.
-Note that such an experiment cannot work without an EPR channel, or, one or more entangled particles.
It's exactly this feature which will see to it, that Particle 3 will immediately respond (with a collapse),
on a measurement far away (in our case: the measurement of Alice on particles 1 & 2).
-Also note that we need a classical way to transfer bits, which encode the state of Particle 1, so that Bob
is able to reconstruct the state of Particle 3 into the former state of Partcle 1.
This can only work using a classical signal, thus QT does NOT breach Einstein's laws.
-Also note that the "no cloning" theorem was also proven here, since just before Bob was able to
reconstruct the state of Particle 1 onto Particle 3, the state of the original partice (particle 1)
was "destroyed" in Alice's measurement.
Well, that's about it. Hope you liked it!




