A few remarkable events or observations, Part I.
Date : 21 March, 2021
Version: 0.9
By: Albert van der Sel
Status: Just starting Part 1.
Remark: Please refresh the page to see any updates.
Here I like to list some events or observations, of which I think that they are "remarkable".
Please note that I cleary state that "it's me", who thinks that they are noteworthy.
But, maybe you would say, that there is nothing special here....
It could be something from science, or, some something which is not confirmed, or possibly
even completely hypothetical (of which it is only certain that many folks would be very skeptical).
But, most subjects will be from Science, so not much "hocus pocus" here, with a few exceptions.
And, occasionally, a few personal experiences (which might be remarkable) will be shown.
Anyway, I will do my very best to avoid subjects which are obviously hoaxes, or pranks, or possibly even
something like harmless "misinterpretations".
I guess, that I only want to list some subjects, which has drawn my attention, and where possibly
no fully satisfying explanation exists for. However, many folks think that there are good explanations.
But some (?) sections will (maybe) not so remarkable at all. Maybe I think they are, but others do not.
Well..., I usualy only bake "patates frites" (french fries), so..... there you have it.
Contents Part 1:
1. Humanoid object on the Moon? (Google Moon).
2. So, what is being transported with "Quantum Teleportation" ???
3. Is Inertial Mass really equal to Gravitational Mass? (Yes, it is).
4. An Encounter With Racism.
5. The best UFO reports (in my opinion) (moved to Part 2).
6. Leviathan Melvillei, the "Super Orca" from the Past.
7. Why some folks say the Universe is "in" or "at" a Black Hole.
1. Humanoid object on the Moon? (Google Moon).
1.1 General description:
You probably are going to doubt my mental sanity, due to the following rather strange subject.
But I tell you, the subject really has one interesting feature, I think. See also section 1.3.
The thing that puzzles me, is that when you rotate/re-angle the image, the "shadow" alters accordingly.
Fig. 1.

If you have "Google Moon", you can see the figure for yourself. Just enter the coordinates 27° 34' 12.83'' N, 19° 36'21.56'' W,
and you will see the object. You can zoom in/out, or rotate etc.. But, Is it really an object?
Almost everybody says, that it is one of the following explanations:
- At the time of the picture was taken, unfortunately, there was some dust or debris on, or near, the lens.
- Maybe it is due to how "Google Maps" assembles the map of the Moon, which indeed comes from various sources.
- It's "wishfull thinking". It's indeed true, that our mind "creates" (fantasizes) an image, which in reality
(when you have more accurate data), is just mudane stuff (like rocks in some configuration,
and only from a distance, it resembles some sort of a familiar figure).
Well, to me it strikingly resembles a Humanoid figure, which really stands out with respect to the other
features on the landscape.
If it would indeed be an existing object, then it would be very large, if compared to the other features
in the landscape. How large, I'am not sure, but certainly far, far more larger than normal human sizes.
By the way, the object is gone (or is not visible), at later observations. Google Moon used lots
of pictures, among others, from the "Clementine project", but other footage as well.
Note:
Google Moon can be started from "Google Earth". I have downloaded "Google Earth Pro" quite some time ago.
From that version, in a sort toolbar at the top of the screen, there is a button with a Saturn-like
picture. If you use that, you can choose to start up Google Moon. From there, you can enter the coordinates.
I strongly encourage you, to take a look at it yourself.
1.2 History:
As it seems, the object was discovered by "Jasenko", using Google Moon, in 2014.
Shortly after, the discovery was put public by "Wowforreeel", using a clip on YouTube.
From there, it started to get known by the public (the part which are interested in such stuff).
I must say that when I look at "Wowforreeel"'s other publications, it's all about strange discoveries
and that kind of stuff. To be honest, it does not seem to be very scientific.
However, the image itself, visible using Google Moon, is real enough, independent of who saw it first,
and independent of any interpretation of that image.
NASA, or the scientific community, never felt any motivation or reason to extensively comment on the image,
which ofcourse makes a strong point for a logical, mundane, explanation of the image.
Note:
It could be, that Google Moon will update the picture database of Google Moon somewhere in the future,
which probably will wipe out the image which is subject of this note.
1.3 Interpretations:
It's almost certain that it's not an Alien creature, or Alien Robot, or something like that.
Suppose, an investigation team spended some serious effort in analyzing the available data,
and came to the conclusion, that the image really shows some sort existing "object" on the surface
of the Moon, at that time the picture was taken.
Then what? The object "looks" a bit humanoid, but it's not a crisp and clear picture.
But what if it was also concluded that the image indeed also resembled a humanoid figure.
Then...., well, I don't know.
More likely, if one is rational, is that one of the 3 explanations listed in section 1.1 applies.
But I personally must say, that none of them is very convicing.
For example, debris on the lens, is not very likely, since then multiple pictures should then have
the same sort of blurr or other disturbance.
Better seems to be the multiple sources of footage, which, by some process, were added in order
to form the full map of the Moon. Indeed, similar effects have occurred at other projects.
So, why am I taking up this subject? Well, it's the shadow. If you observe the image, and rotate a bit,
or just play around for a while, the shadow keeps on being in accordance.
You can take a look for yourself, and check out if I have a point here.
That's just a bit strange.
And that's the whole reason why I have placed this subject in this note.
But do I really believe it's an Alien object (Robot, or something else...)...? Well... no, not really.
I do not rule it out, ofcourse, but it's very, very, unlikely. So, I do not think it's a real humanoid.
However, the image is intriguing. Oops..., I have to say "the image is Remarkable", ofcourse.
But the most reasonable explanation ofcourse, would be one of the three, as listed in section 1.1.
2. So, what is being transported with "Quantum Teleportation" ???
Are it the classical bits, or the Quantum State? Or both? Does the EPR channel "exist", or not?
So what in essence is Quantum Teleportation (QT)? It has been proven to be possible, to teleport
a "property" (or feature) of a particle (or photon), to a remote location, to another
particle or photon.
So, it's not the particle as the whole entity which is teleported, but "just" one Quantum property of such
particle. Two common examples of such properties are "spin" and "polarization".
In better words: It's the "Quantum State", of such property, which is teleported, over possibly
large distances.
The following classical article, published in 1993:
Teleporting an Unknown Quantum State via Dual Classical and Einstein–Podolsky–Rosen Channels (March, 1993)
by Bennett, Brassard, Crepeau, Jozsa, Peres, and Wootters,
really started to set the QT train in motion. It's widely regarded as the classical article on QT.
Since then, much further theoretical work has been done, and many exciting implementations has been realized.
QT has deep ties to other disciplines, like "Quantum Information Theory", and "Quantum Computing".
The proposal by Bennett et al, is often called the "Original Protocol" (OP), and thereafter, over many years since 1993,
many others protocols followed. Either purely theoretical, or also theoretical and with experimental implementations.
Ofcourse, I am no match compared to the active workers in those fields, but maybe I can come up with an interresting
story on the subject.
2.1 The Original Protocol:
-Qubits and Entanglement:
Let's start with the "Original Protocol". It's very common for particles to have a "spin", which is a
sort of angular magnetic momentum. You can visualize it as a spinning ball (which is not entirely correct).
It has turned out, that along a spatial direction, this is spin can be either "up" or "down",
often expressed in the basic states |1> and |0>.
But you might use other symbols as well, like |↑> and |↓>, where such arrows might make
it a bit more explicit. Just a matter of taste, really.
As long as you have not performed a measurement, Quantum Mechanics says that the spin-state of the particle
exists in a superposition of those basisstates, expressed as |φ >= α |0> + β |1>.
This "looks" like a vector addition of the basis states, and mathematically that is indeed so.
However, for the interpretation..., the last words have not been spoken just yet.
The remarkable thing is: the quantum spin-state of the particle, is simultaninously both |1> and |0>,
that is, thus at the same time. That's remarkable, because you might think that it's either |1> or |0>,
and we simply do not know which one, unless we perform a measurement.
But that's not true. According to the Quantum formulation, it's really both states at the same time.
With those two basis states, we further often have in practice that |φ>= 1/√2 |0> + 1/√2 |1>
The coefficients before the basis states, can be associated with the probabilities of finding either state.
That's another "rule" in Quantum Mechanics. Here those coefficients just happens to be 1/√2.
In case of |φ>= 1/√2 |0> + 1/√2 |1>, we would have (1/√2)2 + (1/√2)2 = ½ + ½ =1.
So the sum of all of the probabilities equate to "1", which is what we would expect.
Remember, it's one particle, where we focus on "one quantum feature", which can attain (at measurement)
one of two states. In such case, we have the representation:
|φ > = α |0> + β |1>
which often is called a "qubit". Remember, it's a superposition of the spin "up" |1>, and spin "down" |0> states.
In some cases, the way to write it down, is slightly different, but there is no fundamental difference between all of them,
so, we might see in different articles:
|φ > = α |0> + β |1> (most often used)
|φ > = α |+> + β |->
|φ > = α |↑> + β |↓> (makes the up or down states a bit more explicit, using arrows)
In the OP, a scenario is shown where we have 3 particles. The authors started out with two particles, and
a third one is added at a slightly later time. That third particle, a qubit, is exactly the one from which
the quantum state will be teleported.
The two particles the authors started with, are "strongly entangled", which has a very special
meaning, and consequences. Those two particles are then very different from the third particle,
which is that qubit which is added at a slightly later time.
So, we start with the two particles, which are entangled (with respect to the quantum state "spin").
An entangled system in general, really looks like an "inseparable whole" (with respect to a certain quantum state).
If you would like to consider one particle of an entangled system, you cannot ignore the other one,
since this intertwinement is so "imparative".
Let's take a look at the representation of the entangled system (two particles), which the authors used:
|Ψ1,2 >= 1/√2 . ( |↑1 ↓2> + |↓1 ↑2> )
Instead of the relatively simple |↑> or |↓>, we have |↑1 ↓2> and |↓1 ↑2>
where each of such term, as a basis state, makes it clear that it must be considered as a whole.
Note that we now also must use the subscripts "1" and "2", to differentiate between particle 1 and particle 2.
Also note that the addition of those two states, makes it clear we have a superposition of basis states.
But if we take a look at just one of such state, like |↑1 ↓2>, such a vector
is simply "interwoven" with the quantum spin of particle 1 and particle 2.
This makes "entanglement" such a remarkable phenomenon, instead of just looking at a single particle.
With entanglement, You cannot "factor out", or seperate, the one particle, from the other.
Now, here is a very remarkable piece of stuff: if we seperate the particles, possibly even over a large distance,
the entanglement still remains in effect. In many experiments, distances well over 100 km have been achieved.
-A (perturbive) measurement:
The following belongs to the Quantum formulation, however, the jargon used, is from the "Copenhagen" interpretation.
Be aware that this "Copenhagen" interpretation, is just one of several popular interpretations.
As a side note: I personally like the "Pilot Wave" interpretation a lot, since since it nicely "fits"
rather well for many observations, like the double slit experiment, and many others.
The notion of "measurement", or "making an observation" in Quantum Mechanics, is quite something.
One way of viewing it, is that at microscopic systems, a measurement is highly perburtive.
After the measurement is done, you have a clear result, but does that reflect the original situation,
thus before the measurement was done? Well, no.
Suppose we have |φ > = a |φ1> + b |φ2> + c |φ3>
So, we have a set of 3 basis states (or eigenstates), and the complex coefficients a, b, c, relate to the
probability of finding one of the states φ1>, |φ2>, |φ3>.
Yes, Quantum Mechanics is intrinsically "probabilistic".
For the coefficients (probabilities) it holds that a2 + b2 + c2 =1, so,
the sum of the probabilities add up to "1".
So, |φ > may "collapse" to the basis tate |φ2>, with an associated probability of b2.
In Copenhagen jargon, it's called the "collapse of the State vector".
-A product state of two particles (not entanglement):
Now, suppose we have two non-interacting systems of two qubits|φ1> and |φ2> (close together).
Then their combined state, or "product state" (that is: when they are not entangled), might be expressed by:
|Ψ> = |φ1> ⊗ |φ2>
Such a state is also called "seperable", because the combined state is a "product" of the individual states.
If you have such a product state, it's possible "to factor out" (or seperate) each individual system from the combined equation.
The particles are not intertwined (entangled), since we can decompose (factor out) the product state into
the individual particles again.
It's further not so terribly important for our discussion. However, in a few moments, the product state of all the members
in the Quantum Teleportation setup, will be described. Then we will have a true entangled pair (namely particles 2 and 3),
and an ordinary qubit (particle 3), which will come closer and closer to the entangled pair.
To describe the complete state (particles 1,2,3), we need to use (for a short moment) the "product state".
-An entangled pair of particles:
Let's now take a look at an entangled system as was shown above: Ψ1,2 >= 1/√2 . ( |↑1 ↓2> + |↓1 ↑2> ).
Here we have a superposition as well. So, a measurement may yield |↑1 ↓2> or |↓1 ↑2>.
But, suppose both particles are seperated by a large distance. I could go to particle 2, and measure the spin.
With an ensemble of such entangled particles, I might sometimes find |↑> and sometimes |↓> (for particle 2).
Now, again a large distance, and now I like to see the correlation between particle 1 and particle 2.
A term like |↑1 ↓2>, actually already says it all.
If particle 1 is ↑, then particle 2 must be ↓. Or, If particle 1 is ↓, then particle 2 must be ↑.
That's a bit weird, since how does both particles know that? Especially if the distance is large enough, so that
no signal with the speed of light can inform the other particle, that the first one was measured "so and so".
No serious physicist accepts faster than light information transfer (for now), so something else must be going on
which we still not completely understand. Anyway, such events are called "non-local" events.
At the time I measure the spin of particle 2, then the result of particle 1 is fixed too.
But, at the precise time I perform the measurement of particle 2, the authors of OP, said that we have an EPR channel.
This is not so much a channel for information transfer, but a channel (a label) which describes the interwoven
properties of both entangled particles.
For now, it's best to view such Quantum Channel as a "resource" in Quantum events.
Note that when I indeed measure the spin of particle 2, then the entanglement breaks up, and the EPR channel is gone.
In a Copenhagen-style, you might say that after measurement (of one member particle), we end up either
with |↑1 ↓2> or |↓1 ↑2>, so one measurement
fixes the other member too, not withstanding the fact we had a superposition of both states (before measurement).
If it's still not (relatively) clear: Well, at the start we had 1/√2 . ( |↑1 ↓2> + |↓1 ↑2> ).
So, particle 1 still has a good chance to be in state ↑ or in state ↓.
Remember we have a superposition here, namely the equation above. Now, if we do not measure anything at all, both particles
have a good chance to exist in state ↑ or in state ↓. Or even better formulated:
it's a superposition, so both particles are in in state ↑ and in state ↓, simultaneously.
Now, I measure particle 2, and "suddenly" that fixes particle 1 as well. That's what Einstein called the "spooky action at a distance".
Sorry, it's all a bit Mickey Mouse language, or even worse, Albert's language, but I hope you get the idea here.
Note: the above is not so bad I hope, although I should have said something more about statistical ensembles.
-The setup of the Original Protocol:
Sometimes it is easier to use "Alice" and "Bob", who are the "agents" who sets things in motion.
Bob is near particle 3, and Alice is near particle 2. So, let them do the work for us.
The figure below, might seem quite complex, but that is solely due to the fact that I'am not the best author,
and my own pictures are truly horrible. Sorry Albert..., as Albert, I have to say it's a fact.
And Albert..., maybe it's better for you to take a position as someone who sells "patates frites"...
Fig. 2.
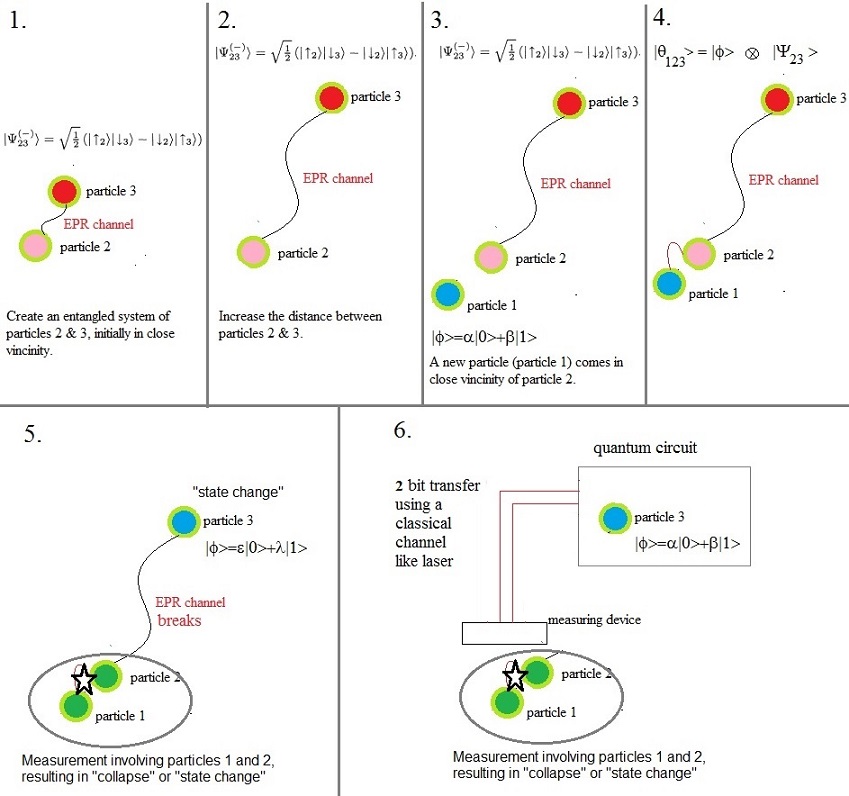
In the figure above:
In (1), we have the entangled pair (particles 2 and 3), relatively in close proximity.
In (2), we increase the distance between them, possibly over hundreds of miles.
In (3), particle 1 (a qubit |ϕ1 > = a |0> + b |1>) comes in to proximity
of particle 2. The exact state of this qubit is not known, that is, we have no clue
of the coefficients "a" and "b".
Is that neccessary? If a state is known beforehand, we do not have "teleportation", but instead
we are "state preparing", which is a different sort of Quantum game.
In (4), particle 1 comes even closer, and now we must describe the full state of
particles 1,2,3, as the "product state" of particle 1, and the entangled pair (particles 2 and 3).
Note that a Quantum Channel, as a resource, "exists" (?) between the entangled particles.
Also, a classical channel, by whatever implementation, like laser, radio etc.. exists, coupling
the locations of particle 2 and particle 3. This is only illustrated in fig. (6).
We are at the phase where the qubit, that is particle 1, is getting closer to Alice's particle.
See (4) for an illustration of this. Now, we need a product state, to correctly describe
the "cluster" of the three particles 1,2 and 3. This might be written like in the following:
|θ123> = |ϕ1> ⊗ |ψ2,3 >
This can be mathematically worked out, and terms rearranged. In itself, that's a bit complex, but
not so terribly interresting. So, we can easily leave out that sort of math.
|θ123> = |ϕ1> ⊗ |ψ2,3 > = (doing some math here...)
≈ Φ12 [ (-a |13 > - b |03 >) + (-a |13 > + b |03 >) + ( a |03 > + b |13 >) + ( a |03 > - b |13 >) ]
-The part: Φ12 is some collective term describing particles 1 and 2.
-The part: [ (-a |13 > - b |03 >) + (-a |13 > + b |03 >) + ( a |03 > + b |13 >) + ( a |03 > - b |13 >) ]
describes particle 3. But do you see that it's a superposition of 4 qubit-like terms, with some combinations
of the coefficients "a" and "b" of the original qubit (particle 1).
Next, Alice performs an observation on het side, or, in other words, she makes a perburvative measurement
relating to particles 1 and 2, thereby breaking the entanglement between particles 2 and 3.
Now, particle 3 is in one of the 4 states listed above, and that's already pretty close.
We do not know which one, but it's already great, since the superposition above, lists the "a" and "b".
To make it exact, Alice had the classical channel in place. Using quantum gates, it's possible
to obtain classical bits, which relate (or reflect) the Quantum state of particle 1, just before thee measurement.
For the classical channel:
Alice might apply a CNOT gate and / or in combination with a Hadamard gate. Or she has another trick
to obtain the two classical bits produced when particle 1 and particle 2 interacted (in a perburvative measurement).
Those two bits, are transferred using an ordinary classical channel, so it might even be by radio, microwave, laser etc..
So, teleportation does not 'break' faster than light law.
Those classical bits, represent nothing more than a phase shift, which Bob uses (again with gates),
to reconstruct a replica of the original qubit.
It's quite spectacular. Note, that we are not cloning the state of the original particle, since this original
state is destroyed at the moment Alice performed her measurement.
What do we have sofar?
-It's possible to quantum teleport a Quantum state.
-There is no cloning, since the original state is destroyed in the measurement at the original.
-Sofar, it's using a classical channel, and a Quantum channel.
Questions:
-Can we do without the classical channel, thus using only a Quantum channel?
-Can we replicate multiple Quantum states at the same time?
-What is the exact state, or description, of a quantum channel?
-How does "non-locality" and a "Quantum channel" relate?
It is suspected that non-locality behaves like "instantaneous", just like when Bob finds "up"
for his particle, immediately dictates what the result for Alice's particle will be, no matter
how much distance exists between Alice and Bob.
Note the word "behaves", since there is no ground for true "faster than light" information transfer.
However, the last 15 years or so, much more insights appeared for effects like "Quantum steering",
so that deserves another piece of text as well. You can find that later in this same note.
So, the most remarkable thing is, what I think, is how entanglement "works".
Is a Quantum Channel (EPR channel), just an abstraction, or what?
3. Is Inertial Mass really equal to Gravitational Mass? (Yes, it is).
It's quite some subject. Although, at first glance, many folks might wonder where the problem is.
I hope to tell you, in this small piece of text.
Be warned though: many, if not all, physicists have good arguments in saying "that they are equal".
For me, the question is still not quite resolved, and all in all..., I find it a Remarkable issue.
Ofcourse, I could be completely wrong. If so, I indeed was better off in having a carreer in selling "patates frites'.
Indeed, I must warn you that most physicists would say that I am on a futile mission.
Yes, "mass" is simply "mass", and sometimes it's labeled inertial, and sometimes gravitational.
That's it. Everybody sees it that way. Albert..., wake up !!!
Also, nummerous experimental tests have been performed, to detect any difference between gravitational mass and inertial mass.
The conclusion sofar: they are equal, to a very high precision (error margin).
However, for "doubters", the central question thus still seems to be: "How and Why are Inertial Mass
and Gravitational Mass Equal, and even Identical.... If indeed so...
Was there any reason to have different "labels" or is it just the context?
Well, sometimes we only see gravity operating on mass, and in many other cases, it's different agents
or fundamental interactions operating on mass, and then we often call it inertial mass.
For inertial mass (MI), on a macroscopic scale, it's that property of an object, to "resist" acceleration.
If an object is at rest, or has a constant velocity, you need to apply a force to change that velocity.
You need to apply a force, and it costs energy, to increase it's speed.
Just as in the example, that you need to apply a force to a steel ball of mass MI , in order to start to get rolling,
and it moves faster and faster, in accordance to Newton's Law "F = MIa" (F: force, MI: mass, a: acceleration).
Gravitational Mass MG, relates to the amount of force, exerted on the object by a gravitational field,
(or gravitational force). In effect, an object accelerates in a gravitational field, like in the exampe
if you would drop an iron ball from a tower. Here we would have "F = MGa" too, here then with "a" equal to
the acceleration due to gravity on Earth's gravity (usually expressed as "g").
It's not difficult for you to say "Case Closed", and then simply refer to Einstein's Theory of General Relativity.
This Theory is centered around Mass-Energy, Curved Space, Acceleration=Gravity.
In effect: There exists an equivalence of Acceleration and Gravitation. Furthermore, an assumption
which forms a basis for this succesfull theory, is that MI=MG.
It's also called the "equivalence principle".
As a side note: Suppose we have a bowling ball and a feather. You are on the Moon (no atmosphere), and from a Tower,
you drop both objects at the same time. Which object hit the Moon's surface first?
Well, both hit the Moon's surface exactly at the same time.
In General Relativity: an object in free fall is subject to no force and is an inertial body moving along a geodesic.
Both objects, the bowling ball and the feather, follow the same like geodesic (sort of shortest path).
So..., Where are the remarkable things? Maybe, the following stuff is indeed remarkable:
1. What about Higgs?
The "rest" mass of fundamental partices (leptons, quarks), are (likely) due to the coupling with the Higgs field.
At least that is true, if we follow the Standard Model of Physics. Indeed, a few years back, the Higgs boson was detected
using LHC experiments at CERN. Also, based on theoretical conjectures, and now also experimental results, the "Higgs case"
is pretty strong. So, we may see that as a fundamental principle of explaining "inertial Rest Mass" of particles.
The Higgs field is everywhere, and a nice analogy explaining the effect of Higgs, is the following.
Suppose you want to cross a room, with not much other people in that room. You can manage that fairly easy.
Now suppose the room is very crowded. Now, you have to take that into account, and it costs much more effort to cross that room.
In the first case, you are like a "light fundamental particle", and in the second case, you are a "heavy fundamental particle".
It's just as if the Higgs field (=the other people in the room) are hindering you in your movements. And if you have little mass,
the effect is small, and a similar reasoning for a large mass.
Ofcourse, it's just a simple analogy, trying to explain the effect of Higgs.
Now, do you see any sort of relation with Gravitational Mass? No, it's a bit hard to do so.
But the problem goes away if MI and MG are Identical. Then they are simply
two names for the same feature.
But even so, there still might be some subtle issues. Fermion condensates, might attribute too
to masses of particles as "certain mesons". All in all, the modern theories are very spicy.
I think it's fair to say that the precise origin of "inertial mass" is not completely determined yet.
And from another angle: If consider macroscopic objects, like Earth traveling around the Sun,
in a sightly elleptic path, then it can be nicely explained with "curved SpaceTime" of General Relativity.
In such perspective, it's no use to talk about Higgs style Nambu–Goldstone bosons.
True, theories of the "large" have not yet reconciled with theories of the "small".
So..., very maybe, really very maybe, it all in all is not conclusive yet to say, that MI=MG.
Remember, I am "Albert" and I usually bake "patates frites" (ok, silly).
But (1), is certainly not enough to say anything usefull, since, again, theories of the "large",
have not yet reconciled with theories of the "small".
2. A simple Thought excercise.
Suppose that MI is not eaxtly equal to MG.
Then there might exist curious situations where MI > MG, or MG > MI.
Even from just a "classical viewpoint", nummerous objects (like atoms, or nuclei), have "stored"
binding energies. For example, in many cases, It takes energy, or mass, to "bind" particles together.
Or, they "loose" energy "somehow", when they form an ensemble (a nucleus).
You can expand such a view, by also take into account, rotational movements, vibrations etc..
which account for energies as well. However, interactions with the environment is a very determing factor,
and we would enter al sorts of conjectures from Thermodynamics. So, let's stick to binding energies only.
For particles, originally at distance, which comes closer to some "nucleus", it usually means that
they enter a potential "well" (a pit), a somehow "loose" potential energy.
But, it can be more complex as sketched above. It's not always a matter of "+" or "-" energy.
However, typically, at a large distance, a particle may be at "0" potential Energy relative to some
to some nucleus, and when it has become part of it, it might be at -100 MeV compared to what it was before.
Anyway, this all is well explained by classical/modern physics.
It can happen that we can speak of a (inertial?) "mass defect".
The actual mass inside, is less than the sum of the individual masses of the (e.g.) protons and neutrons
inside a nucleus, since energy is converted when the nucleus is formed. This energy is equal to "missing mass".
Is there a problem? No No! The Big Boss Einstein already showed us that mass and energy are equivalent.
I only want to say how (sort of) "flexible" internal (inertial?) mass is.
As another example, suppose an object has a constant speed "v", which is a relevant fraction of the speed of light,
with respect to another frame of reference in rest.
If "v" is indeed high enough, the effects of Relativity like time dilation, lenght contraction, but also increase
of the mass of the object, really becomes noticable.
Here too, the increase in energy (with respect to a frame when the object was in rest), translates for a large part
to an increase in mass of the object.
Now, let's take a look at Gravitational mass.
Above we have seen that, when e.g. particles form a nucleus, we will see a "mass defect".
In such similar cases, we are dealing with the Nuclear force, and in other situations,
with the ElectroMagnetic force, or other forces. However, gravity does not play a role,
or the effects due to gravity are unimaginably small.
However, what do we have, when we are dealing with larger objects, like Planets, Stars etc etc..?
What is happening when small masses (due to gravity), lump together, and possibly even a "while" later
form a Planet, or something else, which we call "a large Mass".
Ofcourse we have a similar situation as we already have seen above. However, the smaller particle
at a larger distance, have a larger gravitational energy, compared to the "end result" (like a Planet).
Again, if you add up the gravitational mass of the smaller particles (when they were free),
then that sum will be larger than the gravitational mass of the Planet, because of the mass converted
due the negative gravitational potential binding energies (when the particles lump up).
I think that only a few folks would (possibly) find the following interesting:
Would there be a difference between the inertial Mass of the Planet, compared to the Gravitational mass?
Well, they are identical, so how would one determine the one and the other?
That would be a tough question, perhaps. However, with white dwarf stars, or neutron stars, the possible effect
might be more noticable.
There was not really not any doubt that "mass=mass", but in some occasions, an observable aspect of mass
might differ from another observable aspect of mass. It might just depends on the type of measurement.
Secondly, some quite deep fundamental, and new theories, does not make it trivial from where mass
exactly originates, even if you were only considering elementary particles and the like.
You see? Although this is an extremely short, and simple text, It already becomes obvious that no matter
how you twist "your butt", mass is simply mass, possibly having different "labels", depending on the context.
4. An Encounter With Racism.
I don't have any plan or something, when creating this text (or other texts). I simply remember something
which seems "remarkable", and from there it goes, sort of, in autopilot.
Just now, I remember something which was "very disturbing"...
I don't like to talk about myself. However, this stuff is remarkable. "Remarkably Bad" that is.
So, I like to share it in this note. It cannot hurt to do so.
No, I myself, was not a victim of Racism. But I saw a strange form of racism, and it was "real".
To this day, I still cannot fully explain it. Anyway I like to talk about it. Well, only here, that is.
Ofcourse I have seen racism on some occasions, especially the "subtle" forms, which are very Evil as well.
For example, a manager, who rejects a certain applicant for a job, where the rejection was clearly motivated by the roots
of the applicant, while the capacities of that person were outstanding for the job.
Such things happens all the time, in Europe too, even in The Netherlands which is where I live.
This story is a bit different. Somewhere in the '90's (1995), I was "somewhere" in Afrika, doing contracters work,
but personally I was there for studying nature and wildlife in the weekends (most often I was free during weekends).
The chance for going to special places, was my main motivation to take this temporary job.
(I do not want, or like, to be more specific on locations).
I was somewhere scouting for wildlife, when I suddenly saw three kids. They were white, and I was
a bit amazed, since they had sidearms (not rifles, but pistols in holsters). All three of them.
Having pistols in holsters is a bit strange, especially with kids.
Two girls, and one boy. Maybe they were 17, or 18 or something. Anyway, in that range, and thus very young.
At first, the conversation was not too bad, since it was solely about the landscape and how beautiful
it all was. Then, it turned out that I was actually tresspassing, since this land belonged to their parents.
But they did not made a big deal about it. Then the boy said that "I was from the good race" or something like that.
So, all was OK according to the boy. Then it became really bad. What I understood was that they would
have immediately shot anyone having the "wrong" color. Then those three started talking the worst racist stuff,
for several minutes or so, that I ever heard.
I sensed that this all was for real. Not a joke. It was not some sort of bragging, or something like that.
The girls nodded in all seriousness, on every word the boy spoke. Those three kids, "looked normal",
in appearance. They really looked normal, just like the kids you see in your streets.
But they were as evil, or distorted, as hell itself.
At those moments, I was not particularly scared. Only a bit upset.
Not much later, I was alone again. I remember that only from that point on, I was feeling a bit dizzy or something.
It's utterly strange to hear kids talk like that. It has a hard impact, if you know those kids meant every word of it.
There are much worse things ofcourse. All those Wars, poverty etc... The list is endless.
But at that occasion, I personnaly witnessed what an extremely bad education, and brainwashing,
ultimately can do with kids. It's rather terrifying, to see it for yourself.
And, It's remarkble how easily a sort of "nazi kids" can come into existence.
You really see the Devil at work. Maybe the kids themselves cannot help it? They probably can't.
If you think this is all fantasy: No, I shit you not. This was all for real. It really happened.
Somewhere around 1995, in a remote country.
I placed it in this note, since I believe it's a Remarkable Event. Well, for me it was.
But it was not even "that special" or something. Countless of other folks, have seen similar things.
5. The best UFO reports (in my opinion).
Unfortunately, I found out (the hard way) that this subject takes quite a bit of time.
At least, if I want to honour the title "the best UFO reports".
Most sightings and reports, have a "mundane" cause, like militairy aircrafts, balloons, drones, planet constellations etc..
However, without any doubts, there indeed exists a minority of very intruiging reports.
To select and study "the really good ones", is quite labor intensive.
I will come back to this subject at a later moment, namely in Part 2. Sorry for this.
6. Leviathan Melvillei, the "Super Orca" from the Past.
This section cannot be interesting, if you are not amazed by "Raw Power" in the Animal Kingdom.
Well, most people seem to be familiar with the landbased predators from the past, like T.Rex, Deinosuchus, Spinosaurus etc..
Possibly, the true Marine predators from the past, are somewhat lesser known.
For example, Predator X (likely to be "Pliosaurus Funkei"), Kronosaurus, Shonisaurus, Liopleurodon,
Mosasaurus (Hainosaurus or Tylosaurus proriger etc..), Basilosaurus, and Megalodon. And ofcourse, many others....
Some names were actually lables for families of subspecies (like mosasaurus).
Yes, there were many other powerfull Marine predators too. As an example may serve "Zygophyseter".
I believe that "Zygophyseter", and others, were a bit too small in lenght and weight, to count them among the
real heavy weight predators, as for example "PredatorX". That's why I left them out.
The predators which roamed the land, are generally smaller, and less in weight, compared to the large
Marine predators.
If you like, you can google for "Pliosaurus Funkei" (at first called "Predator X", when at that time it was
not sure it belonged to the Pliosaurus species). Or google on Mosasaurus, for example, to see another "monster".
Enormous large, and powerfull predators, for sure.
So, what is "Remarkable" in this section? It's the predator which goes by the name "Leviathan Melvillei".
It's a mammal and thus quite different from the others in the list above, and it's remarkable (I think),
by having some special features.
Estimations of it length varies between 13.5m and 17.5m, while it's max weight is estimated to be 50 tons.
But even if it was more generally to be in the order of 30 tons, then it still was enormous.
If you know that T.Rex was just (about) 7 or 8 tons....
And, Leviathan was a real predator. A skull of about 3.5m, and teeth of about 36cm, and from the skull
it can be deduced that it's biteforce was unprecedented.
For example, If we claim that PredatorX, and similar, probably have a bite-force of several times that of T Rex,
then for Livyatan, it must have been out of scale.
Also, scientists believe that Leviatjan, possibly used his "head" as a Ram, to slam it's victims uncouncious.
Basilosaurus, and Leviathan, were mammals, and generally classified as whales.
Leviathan is very remarkable, since it has many features you may associate with Orca's.
They most likely lived in packs. Ofcourse, they had echo location (sonar), next to the other senses,
which greatly enhanced their abilty to scan the environment, and also to look for prey.
They were mammals, so, for their brain capacity..., we can only speculate.
What could have been on the menu? Well, other whales, sharks, and I believe it could have been anything.
One individual animal was invincible in the Oceans, but a pack of them is Undescribable....
So, what was exactly remarkable here? I think that Leviathan Melvillei was the "Super Orca" from the past.
I you just think how effective a pack of Orca's is... then imagine a pack of Leviathan's.
I think that this "Super Orca" from long long ago..., is really remarkable.
Ok, sometimes I behave like a 7-year old at occasions... (Well, at occasions...??????)
There exists many pictures and sketches of Leviathan. Why not google around for a bit?
Note:
Leviathan lived in about the same time, as Megalodon. Were there any encounters? Or were they too much seperated,
in location and/or time? No, actually they might have run into each other.
In a way, it's probably good that we will never know how such encounter ended.
- Clip about the discovery of Leviathan.
- Some other info on Leviathan.
7. Why some folks say that the Universe might be "in" or "at" a Black Hole.
I already created a very simple, general note on Black Holes, which might be useful to read first.
If you like to try it, then use this link.
Anyway, in that note some basic things will be shown as the Bekenstein/Hawking relation, and stuff
like the Chandrasekhar limit, and some stuff on metrics.
Especially, using Bekenstein/Hawking, it is "nice" to see that "only" the "Surface A",
defined by the event horizon, seems to determine the "information" (entropy) associated with the Black Hole.
That note should also provide some insights in a general sense. Singularites, but also Kerr BH's etc..
What is pretty cool, I think, are the observations done sofar, like the footage of the Massive black hole in M87 etc...
It's only a recommendation (strong recommendation) to take a look, but you can ofcourse also skip it.
But that note is not really a prerequisite for this section.
So, what is this stuff, all about....? And why does Albert, the "patates frites" baker, has put it in his note?
The last question is easy: It's remarkable stuff !!!
There are multiple Cosmological models, describing our Universe. We simply do not know for sure, which one
approaches "reality" best, if at all. Ofcourse, the "Standard Model" is the most accepted model for now.
However, there are a few models which are candidates too, but insufficient data exists to support
them as possible correct models. One such model, describes our Universe as "being" a sort of reality
"near" (at?) the interior of a Black Hole. A description like the former sentence is not really adequate,
as you will see shortly. For now, it's all purely theoretical work.
Some famous names of scientists (partly) involved, are 't Hooft, Susskind, Thorn, Maldacena, and many others working
in (mainly) theoretical Physics.
As an example of other folks in the field, then I may say that the conjectures of Ryu and Takayanagi are very important too.
An older basis, forms the Bekenstein and Hawking relation, from 1974.
All those folks listed above, have done tremendously more work, in many fields, but were also involved,
in the rather "fantastic" model which I hope to describe below.
=> (1). Bekenstein and Hawking relation.
Somewhere around 1974, both Bekenstein and Hawking were involved in producing a relation for the Entropy (S)
of a Black Hole, mainly based on Thermodynamical considerations. It looks like:
|
S
|
= |
kB * A
-------
4 * Lp
|
Now, the Entropy "S" is a measure which gives us information about the number of microstates (or states),
which we can associate with a system.
The curious thing though, is that the formula above, relates "S" to the Surface Area "A", defined by
the event horizon of the Black Hole. Well, it would not have been abnormal, if you would have expected
that S was proportional to the "volume", that is, the region bordered by the event horizon.
But, that is not so. "S" is proportional (according to Bekenstein and Hawking), to the Surface Area.
If you find that a bit weird, then you are not alone.
So, you might say that information is "stored" at (?) or near (?) that Surface Area, and the "inside"
of the Black Hole, seems to fall a bit outside the discussion. Remarkable? Yes!
Folks have also noticed, that we see here a form of "Dimensional Reduction", since a Surface
is one dimension less from a Volume. That's a significant finding.
It's remarkable how something can be expained (if the theory is correct), by "peeling off"
one metric dimension.
=> (2). A simple analogy of "The Holographic Principle in Physics".
Maybe the first one formulating the Holographic Principle in Physics, was 't Hooft.
By the way, he wrote so many stuff on so many subjects, that's impossible to keep track of it.
The Holographic Principle can be illustrated by using a common (earthy) example of "photographic holography".
Suppose you scan an object with a laser, and let the reflected beam interfere with another beam, while
both the beams then combine and interfere, and fall onto a photographic plate.
Then a remarkable effect will occur. This interference pattern is recorded on the holographic plate.
A three-dimensional image of the object will then be observed if the recorded holographic plate
is exposed to coherent light. Then you will see a Hologram of the object.
You have a two dimensional (2D) object, but you see a 3D figure.
Inspired by the Bekenstein relation, could it also be applied to the Universe?
That is, could a (N-1) dimensional reality, generate a N dimensional Hologram, which only corresponds
to that reality (or is connected to that reality)?
Such an idea, combined with the view of Bekenstein of a Black Hole's entropy (number of states),
already "slightly" seem to point towards the idea that the Universe might be "in" or "at" a Black Hole.
Ofcourse, those ideas's above are by no means sufficient. So it's needless to say that we need more solid pointers
that sustaines such a view.
Note:
The true circumstances near a BH's event horizon, might be very complex. For example, time dilation
is enormous, as well as severe Quantum Mechanical puzzles (like what happens with wave descriptions
of particles near the event horizon etc.. etc.. So, the picture I present here, is actually hopelessly
simplified. Also, using Holographic Principle can hardly be done without string mathematics.
=> (3). A few words on The conjectures of Ryu and Takayanagi:
Like all advanced articles, they are pretty tough to read, and that hold also for the works of Ryu and Takayanagi.
But not all is lost.
Instead of chewing on hard math, the conceptual ideas's are far more important.
-

