| US: | SI: |
| 1 pound | 0.4535 kilogram (Kg) |
| 1 grain = 1/7000 pound = 0.000143 pound | 0.00006476 Kg |
| 1 feet | 0.305 m |
| 1 yard | 0.914 m |
| 1 ft-lbs | 1.355 Joules |
| 1 bar = 0.987 atm | same units used |
| 1 bar = 100000 Pascal | same units used |
| 1 psi = 6895 Pascal pound per square inch |
0.689N/cm2 6894.7 N/m2 |
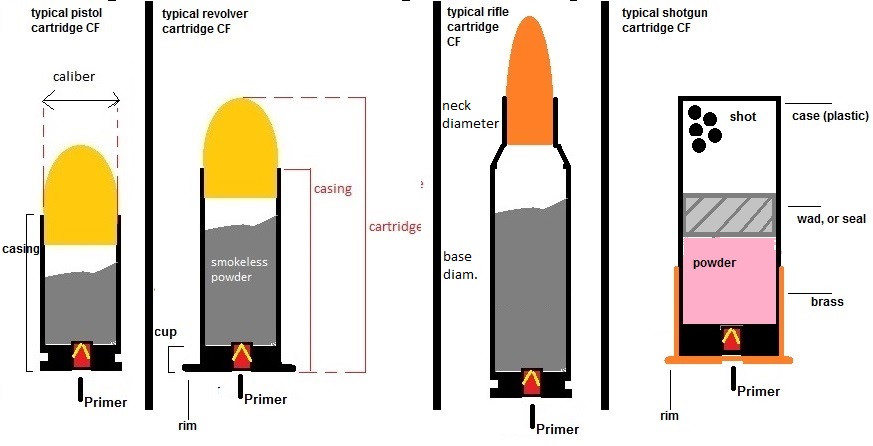
| Bullet diam. | .313 inch | 7.94 mm |
| Neck diam. | .3365 inch | 8.55 mm |
| Base diam. | .337 inch | 8.6 mm |
| Case length. | .680 inch | 17.3 mm |
| Gauge: | Bore diam. inch: | Bore diam. mm: |
| 10 | .775 | 19.69 |
| 12 | .725 | 18.42 |
| 16 | .665 | 16.89 |
| 20 | .615 | 15.62 |
| 28 | .545 | 13.84 |