In the series: Note 12.
Subject: Vector calculus / Linear Algebra Part 1 (introducing vectors).
Date : 16 June, 2016Version: 0.3
By: Albert van der Sel
Doc. Number: Note 12.
For who: for beginners.
Remark: Please refresh the page to see any updates.
Status: Ready. But I will add more sections to this note.
This note is especially for beginners.
Maybe you need to pick up "some" basic "mathematics" rather quickly.
So really..., my emphasis is on "rather quickly".
So, I am not sure of it, but I hope that this note can be of use.
Ofcourse, I hope you like my "style" and try the note anyway.
Preceding notes, which are all ready:
Note 1: Basic Arithmetic.
Note 2: Linear Equations.
Note 3: Quadratic Equations and polynomials.
Note 4: The sine/cosine functions.
Note 5: How to differentiate and obtain the derivative function .
Note 6: Analyzing functions.
Note 7: The ex and ln(x) functions.
Note 8: Primitive functions and Integrals.
Note 9: Complex numbers.
Note 10: Differential equations Part 1.
Note 11: Functions with two or more variables.
This note: Note 12: Vector calculus / Linear Algebra Part 1.
For Vector calculus / Linear Algebra Part 2: please see note 16.
Each note in this series, is build "on top" of the preceding ones.
Please be sure that you are on a "level" at least equivalent to the contents up to, and including, note 11.
Chapter 1. Introduction "vectors" and some elementary algebra:
Often, vectors are introduced as mathematical "objects" having both a "magnitude" (which is the length),and "direction".
As you know, a "scalar" is just a number, or value. For example, the temperature at some location, or the mass
of an object, or the charge of some particle etc.. You cannot "associate" a direction to these examples.
Although math has rather complete theories on vectors, physics is full of real vectors.
In physics, indeed many examples are available, such as "forces", "velocities, "vector fields" etc..
1.1. Representation of vectors in R3:
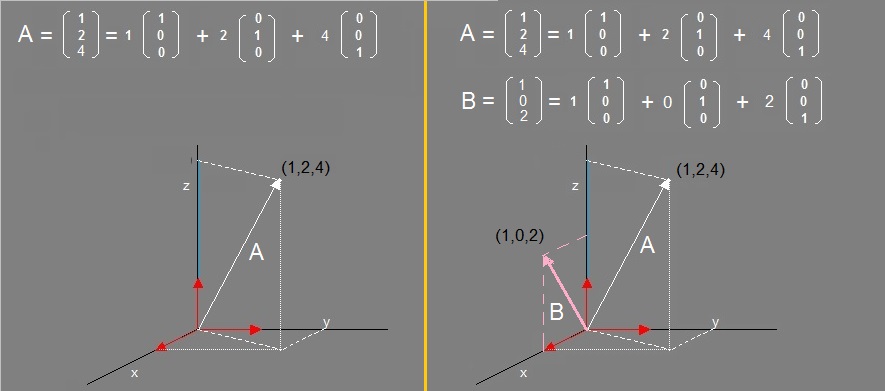
In a Cartesian coordinate system, we can represent vectors, by "arrows" from the Origin, to a certain point (x,y,z).In figure 1 below, you see some vectors in three dimensional space R3. Let's take a look at, for example, the point (1,2,4).
You can see the "arrow" from the Origin to (1,2,4). It has a direction in space, and a certain magnitude (it's lenght).
In any orthogonal Cartesian (flat) Space, say of dimension "N" (so having N axes), we can identify points as n-tuples,
like (x1, x2, .., xN).
Figure 1. Some examples of Vectors in a Cartesian coordinate system.
Indeed, for example, by a long time, we know from former notes, that in R2, we have points like (x1, x2),
but they are usually written as (x,y).
Also, socalled "unit-vectors", or "basis-vectors" are defined, which are positoned along the axes, and having
a length of "1". So, in figure 1, we have 3 unit-vectors, positioned along the x-, y-, and z-axis.
In figure 1, those are represented by the "red" arrows.
Since the x-, y-, and z axes are perpendicular, so are those unit vectors to each other.
We may write vectors as an "n-tuple" like for example (1,0,2), or in column notation like shown in figure 1.
A key point is, that we can represent any vector in R3 (or any space RN), as a linear combination (a sum)
of those unit-vectors.
Thus for vector B in figure 1, we may write:
B = (1,0,2) = 1 (1,0,0) + 0 (0,1,0) + 2 (0,0,1)
It means that we sum:
1 x (1,0,0) ( is the unit-vector along x-axis) +
0 x (0,1,0) ( is the unit-vector along y-axis) +
2 x (0,0,1) ( is the unit-vector along z-axis).
Note that vector B has no "y component", so that's why we have "0 x (0,1,0)". Also, often the multiplication symbol "x" is left out too.
Note:
Many textbooks, articles, uses special characters to denote vectors, like using a letter with an additional arrow on top,
or a range of other symbols. Here I will just use Capital Letters.
1.2. Addition and subtraction between vectors:
Let's stay in R3 for a while. Suppose we have the vectors A and B, where:| A = |
┌ a1 ┐ │ a2 │ └ a3 ┘ |
| B = |
┌ b1 ┐ │ b2 │ └ b3 ┘ |
Then, let's calculate the "sum" of those vectors C = A + B
| C = |
┌ a1 ┐ │ a2 │ └ a3 ┘ |
+ |
┌ b1 ┐ │ b2 │ └ b3 ┘ |
= |
┌ a1 + b1 ┐ │ a2 + b2 │ └ a3 + b3 ┘ |
So, simply add all corresponding x-, y-, and z-components.
Ofcourse, the same principle applies for any orthogonal cartesian frame of reference, of any dimension.
Example 1: addition of vectors in R3
Suppose that we have:
| A = |
┌ 2 ┐ │ 1 │ └ 5 ┘ |
| B = |
┌ 2 ┐ │ 2 │ └ 1 ┘ |
Then C=A+B is:
| C = |
┌ 2 + 2 ┐ │ 1 + 2 │ └ 5 + 1 ┘ |
| C = |
┌ 4 ┐ │ 3 │ └ 6 ┘ |
Example 2: addition of vectors in R2 (the XY coordinate system)
Nothing changes really in comparison wiyh example 1 above. However, vectors in the XY coordinate system
are easy to draw, so I can nicely illustrate vector addition.
Take a look at figure 2 below.
Figure 2. Adding two vectors in R2 (the XY coordinate system).
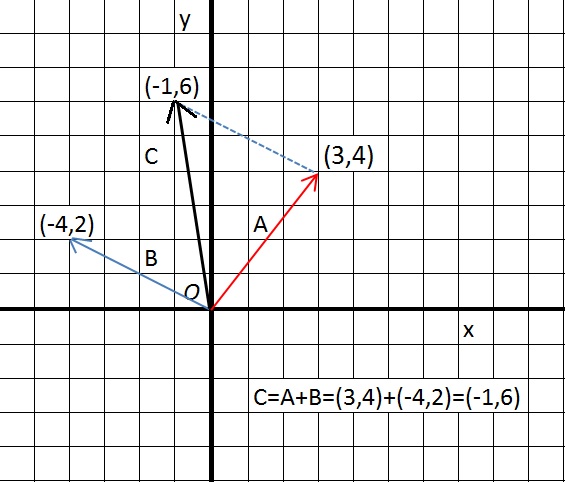
As you might see in figure 2, we have C = A + B = (3,4) + (-4,2) = (-1,6).
Or, in column notation as we did in example 2:
| A = |
┌ 3 ┐ └ 4 ┘ |
| B = |
┌ -4┐ └ 2 ┘ |
Then C=A+B is:
| C = |
┌ 3 + -4┐ └ 4 + 2 ┘ |
= |
┌ -1┐ └ 6 ┘ |
If the vectors A an B in figure 2, would represent physical Forces, then C would be the resultant Force.
In effect, if there was a certain mass in the Origin, while Force A and B were operating on it, then
it would be exactly the same is if only C was working on that mass.
In that sense, C acts as if it completely replaces A and B.
Or stated differently, C is the vectorsum of A and B. We only need to consider C if we would study that system further.
Here is an example you can work out for yourself. The advantage of this exercise is, is that the "direction" of the
resultant force seems completely "natural". Suppose we have the points (-1,2) and (1,2). From the origin, you can
draw a vectors A and B to these points respectively. Suppose they represent Forces. The resultant force then,
can be represented by the arrow to the point (0,4). This time, the resultant force is exactly "in the middle" of A and B.
and makes it symmetrical, just as you probably would expect in this example.
Note:
I am not great in webprogramming. You know, I just do everything with "vi" or "notepad", depending on the platform.
Yes! It shows. I know that my pages are horrible in formatting and how they look. Sorry for that.
Especially with older browers it can be a mess.
1.3. The magnitude or length of a vector:
The "length", or "magnitude", of vector A, is often denoted as |A|, but many other notations go around too.Take a look at figure 2 again, and focus on vector A. Is it not immediate obvious that:
|A|=√(32 + 42) = 5
Yes, for example, again you can apply the "Pythagorean theorem" here, since the vector A, and the sides
along the x-, and y-axes, form a right-angled triangle.
It also is true in any orthogonal Cartesian frame of reference, of any dimension.
In R2, the length of vector A is |A|=√(x2 + y2)
In R3, the length of vector A is |A|=√(x2 + y2 + z2)
In RN, the length of vector A is |A|=√(x12 + x22 + .. + xN2)
1.4. Multiplication of a vector with a scalar:
You can multiply a vector with a scalar number. This is simply defined as that youmultiply all components with that scalar. Suppose we have vector A as:
| A = |
┌ a1 ┐ │ a2 │ └ a3 ┘ |
Also, suppose λ is a scalar.
Then
| λ A = |
┌ λ a1 ┐ │ λ a2 │ └ λ a3 ┘ |
If you take a look again at figure 2 above, en if you would multiply vector A with 3, then it would get "3 times as long":
| 3 A = |
┌ 9 ┐ └ 12┘ |
Note that if you let vary λ along all values of the Real numbers, you can actually "describe", or "reach",
any point along the (infinite) line, where vector A is aligned on.
1.5. Notation of the unit-vectors:
In row notation, in R2 we have the unit vectors (1,0) on the x-axis and (0,1) on the y-axis.Also, in row notation, in R3 we have the unit vectors (1,0,0) on the x-axis, and (0,1,0) on the y-axis,
and (0,0,1) on the z-axis.
You know that you can write them in "column" format too, ofcourse.
In orthogonal Cartesian coordinate systems, there is no difference between the "row" and "column" way of notating vectors.
However, in some coordinate systems we can distinguish between covariant and contra variant vectors, in which case
the format does matter. This will not be discussed in this note. See note 16.
Many textbooks reserve special symbols (letters actually) for those unit vectors. Depending on the Country, and language,
you can encounter many sorts of symbols.
I like to give an example of such practice. Some textbooks use for example:
in R3:
êx = (1,0,0) for the unit vector on the x-axis.
êy = (0,1,0) for the unit vector on the y-axis.
êz = (0,0,1) for the unit vector on the z-axis.
in R2:
êx = (1,0) for the unit vector on the x-axis.
êy = (0,1) for the unit vector on the y-axis.
But many other symbols go around too. One other often found notation,
is by representing the unit-vectors by i, j and k
Ofcourse it can be very handy to have such a short notation for basis-vectors, in many occasions.
So, as a recap, for example in three dimensional space, a vector can be written as below:
| A = |
┌ a1 ┐ │ a2 │ └ a3 ┘ |
= | a1 |
┌ 1 ┐ │ 0 │ └ 0 ┘ |
+ | a2 |
┌ 0 ┐ │ 1 │ └ 0 ┘ |
+ | a3 |
┌ 0 ┐ │ 0 │ └ 1 ┘ |
Or as:
A = a1 êx + a2 êy + a3 êz
Chapter 2. The Inner product and the Cross product :
What we saw in section 1.4, was "no more" than the multiplication of a vector with a number λ.That simply shortens (λ < 1) or lengthens (λ > 1) that vector (unless λ=1, ofcourse)
Two main types of true vector products exist:
-The "inner product" of two vectors, which produces a number.
-The "cross product" of two vectors, which produces a vector again.
Both types have a pretty cool interpretation, as you will see.
However, I consider section 2.2, about the "cross product", as optional reading.
2.1. The Inner product or "dot" product:
Suppose, in R3, we have the vectors A and B, where:| A = |
┌ a1 ┐ │ a2 │ └ a3 ┘ |
| B = |
┌ b1 ┐ │ b2 │ └ b3 ┘ |
Then the "inner product" (also called "dot product") is defined to be:
| A · B = |
a1b1+a2b2+a3b3 |
So, you simply multiply the corresponding vector components. It's that simple.
Example:
Let A and B the vectors:
| A = |
┌ -1┐ │ 0 │ └ 2 ┘ |
| B = |
┌ 1 ┐ │ 2 │ └ 2 ┘ |
Then the "inner product" is:
| A · B =-1 x 1 + 0 x 2 + 2 x 2 = -1 + 0 + 4 = 3 |
In R2, it goes in a similar way. Here the vectors each have only two components.
In general, in a space of N dimensions (RN), we would have:
| A · B = |
a1b1+a2b2+ ... + aNbN = Σi aibi |
The last term, we use the "Σ" symbol, which is a shorthand notation for a summation "over" i, where i runs from 1 to N.
Interpretation of the inner product:
If B is a unit vector, then "A · B" is simply the length of A along the corrsponding axis of that unit vector.I will make that likely first, and then go to a general statement.
Take a look at figure 3. Here we see vector A again from figure 2.
Figure 3. The projection of A on the x-axis. Or, the inner product of A with (1,0).
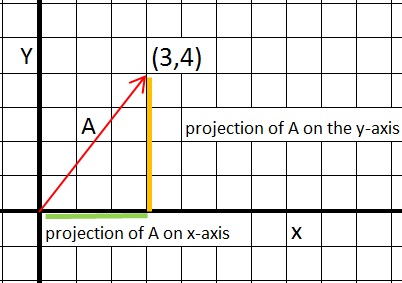
The green linesegment, is exactly the x component of vector A.
It has a length of "3". It's the length of the "projection" of A on the x-axis.
The orange linesegment, is exactly the y component of vector A.
It has a length of "4". It's the length of the "projection" of A on the y-axis.
Let's calculate the inner product of A with (1,0) and (0,1) respectively.
Using the shorthand notation for unit-vectors in R2, let's calculate the inner products:
A · êx = 3 x 1 + 4 x 0 = 3.
A · êy = 3 x 0 + 4 x 1 = 4.
You see that? The "inner products" relates to the length of A on the x-, and y-axes.Well, at least from this example, the "interpretation" is correct.
There is another important equation for the inner product of the vectors A and B.
From note 4, which dealt on the sine and cosine functions, you know that "the length of the green line"
as shown in figure 3, corresponds to "|A| cos(α)", where α is the angle between A and the x-axis.
Note that this relation is equivalent to "|A| |êx| cos(α)", where |êx|, thus the "length"
of êx, is "1".
Although not really proven (but made likely), we have now as the projection of vector A on the x-axis:
|A| |êx| cos(α)
So, then:
A · êx = |A| |êx| cos(α)
So, it might be seen as plausible, that in general for any two vectors A and B, we have that:
A · B = |A| |B| cos(α)
This is a most useful relation to calculate the inner product of any two vectors A and B, given thatyou are able to determine the lengths |A| and |B|, and the angle between those two vectors.
If vectors are perpendicular, their inner product is 0:
For example, take a look at the unit vectors in R3We know that:
êx = (1,0,0) for the unit vector on the x-axis.
êy = (0,1,0) for the unit vector on the y-axis.
êz = (0,0,1) for the unit vector on the z-axis.
So, lets try:
êx · êy = 1 x 0 + 0 x 1 + 0 x 0 =0
You can try that for the others too. Indeed, the unit-vectors are perpendicular, since they
ly on the x-, y- and z-axes.
It is not only true for basis vectors. If any two vectors are perpendicular, the inner product is "0".
Take for example the perpendicular vectors A=(-1,2) and B=(2,1) in the XY coordinate system.
Then:
A · B = -1 x 2 + 2 x 1 = -2 + 2 = 0
You may also interpret the result "0", as that the length of the projection of A on B, is "0", which ofcourse
is true for perpendicular vectors.
You can also deduce it from "A · B = |A| |B| cos(α)", since if A and B are perpendicular, then cos(α)=0.
2.2. The "cross" product:
This "vector product" called "cross" or "outer" product, is only possible (or valid) in three-dimensional space R3.The cross product of two vectors, is a new vector.
This is very different from the inner product, since that returns a scalar.
For the time being, the inner product is much more important to us, than the cross product.
So, we are not going to spend much time on this particular subject. I only mention it, so that at least
you are aware of it's existence.
But it is used often in "physics". Some nice examples exists, and here I will use one such example.
Now make a mental picture of this: if you have 2 vectors, you can always identify a "plane" where both
vectors are in. The vector which is called the "outer product" vector, is always perpendicular to that plane.
Let's spend a few words on a subject in Physics.
Suppose we have a charged particle, which moves with a certain velocity "V".
Velocity has a magnitude (the speed) and a direction, and thus it can be described by a vector.
Suppose further, that this particle moves through a Magntic field "B".
It's just a experimental fact (and backed by the Theory of Electrodynamics), that the particle then experiences
a Force, which is always perpendicular to the plane identified by "B" and "V".
I am not much of an artist, but I tried to illustrate that in figure 4 below.
Figure 4. The force on a charged particle, moving in a Magnetic field.
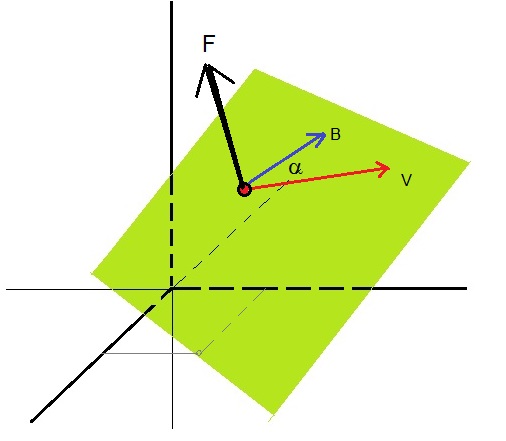
It's remarkable that the Force vector is perpendicular to both the particle's motion and B field.
But it's an experimental fact. Also, in fact we have a compound Electro-Magnetic field, as Maxwell proved
in his theories, and those theories explains the observed behaviour, which is outside the scope of this note.
Keypoint however, that in physics the vector relation is:
F = q V x B
Where F=Force vector, V=Velocity vector, B=Magnetic field vector, and q (which is scalar), is the charge of the particle.
For who is interested, the magnitude of F is F = q vb sin(α)
where "v" is the magnitude of V, b is the magnitude of B, and α is the angle between V and B.
The vector product is called "cross product" and implies a third vector (in this case "F") perpendicular to both other vectors.
In Mathematics (linear algebra):
Mathematically, the outer product or cross product of two vectors A and B is defined as the vector C,
for which the following holds (in R3):
Let vector A be:
| A = |
┌ a1 ┐ │ a2 │ └ a3 ┘ |
And let vector B be:
| B = |
┌ b1 ┐ │ b2 │ └ b3 ┘ |
Then, C = A x B is:
| C |
= |
A x B |
= |
┌ a2b3-a3b2 ┐ │ a3b1-a1b3 │ └ a1b2-a2b1 ┘ |
The magnitude (or length) of C is:
|C| = |A x B| = |A| * |B| * sin(angle A,B).
Even at this point, I consider this note already to be "fairly usable"
if you were really new to this subject.